风电机组对电力系统暂态稳定性影响分析
郝元钊, 李培强, 李欣然, 毕正军, 王 玲
(湖南大学电气与信息工程学院, 长沙 410082)
风电机组对电力系统暂态稳定性影响分析
郝元钊, 李培强, 李欣然, 毕正军, 王 玲
(湖南大学电气与信息工程学院, 长沙 410082)
风电机组作为环境友好型发电的最大来源在电网中的规模日益扩大,必将影响电力系统的稳定性。文章首先对比了恒速异步(CSWT),双馈变速(DFIG)及直驱同步(DDSG)等市场上广为应用的三种风电机组的结构,分析了各个机组的降阶数学模型;通过一款基于Matlab的电力系统分析工具箱PSAT研究了不同故障持续时间下的风电机组暂态稳定性和系统暂态稳定性,对三种机组及其系统的暂态稳定性进行了分析对比;最后讨论了风力发电机组参数对机组暂态稳定性的影响,得知,发电机参数Rr的增加和Xr、Xs的减小有利于恒速风电机组暂态稳定性的提高,Xm、Rs对机组暂态稳定性影响不明显。
电力系统仿真工具箱; 风力发电机组; 发电机参数; 暂态稳定
当前,低碳排放已成为世界工业经济发展的必然趋势。风力发电,太阳能光伏发电等新能源技术在电网中所占的比重将越来越大。风电场规模的不断扩大势必会对电力系统的动态稳定性带来广泛而深入的影响[1~5]。不同的风电机组类型,不同的风力发电机参数,不同的电网负荷模型等因素对电网故障下暂态稳定性的影响是多样的。为了更透彻的了解和利用风力发电技术,研究这些因素对电力系统暂态稳定性的影响十分必要。
文献[6]根据风电场不同容量下的系统稳定情况提出风电场绝对安全容量的概念。文献[7]概述了目前投入市场的各种不同类型的风电机组,详细讨论了其不同的结构、原理及彼此相应的对比。针对双馈型风力发电机组,文献[8]提出利用暂态稳定指标η与极限切除时间CCT(critical clearing time)共同来评估系统的暂态稳定性。文献[9]基于功角,频率两种稳定判据,提出一个在两种运行方式下,采用3种扰动方式的风电场极限穿透功率计算方法,并通过仿真得到影响该系统并网容量的主要因素是频率波动的结论。文献[10]介绍了双馈感应发电机与直驱同步发电机两种变速风机的数学模型,并通过比较模型对风速的响应数据与实际中测量的响应数据,证明了模型的可用性。但上述文献都没有对不同类型风电机组本身的暂态稳定性及系统的暂态稳定性进行对比研究。
本文利用基于Matlab的电力系统分析工具箱PSAT建立了含风电机组的39节点系统模型。通过对比严重故障下,恒速异步、双馈变速、直驱同步等三种类型风电机组的不同响应,分析了机组本身的暂态稳定性及其对系统的暂态稳定性影响,并讨论了发电机参数对机组暂态稳定性的影响。
1 风电机组的数学模型
本文的风电机组数学模型来源于文献[11],主要分3种,分别是恒转速的笼型异步发电机、变转速双馈型异步发电机与变转速直驱型同步发电机。由于本文所讨论的风电机组适用于电力系统动态仿真,因此必须满足以下基本假设:(1)忽略磁饱和;(2)磁通正弦分布;(3)除铜耗外,不计其他任何损耗;(4)基频下定子电压电流正弦分布。
1.1 恒速风电机组模型
恒速风电机组采用笼型异步发电机,模型的基本结构如图1所示。

图1 恒速风机的基本结构
模型主要包含风速模块、风轮模块、轴系模块、发电机模块。其中风速模块采用威布尔分布描述,轴系模块用两质块模型表示,风轮惯量与整个发电机转子惯量通过轴系相连,用如下微分方程表示:
(1)
(2)
(3)
式中:f为电网额定频率;γ为两质块转轴的角度偏移量;ωt与ωm分别表示风轮转子转速与发电机转子转速;Ht与Hm分别为风轮转子惯性时间常数与发电机转子的惯性时间常数;KS为轴系刚度系数。发电机模型采用笼型异步发电机,模型方程为
(4)
(5)
(6)
(7)
(8)
(9)
P=vdid+vqiq
(10)
(11)

1.2 双馈风电机组模型
双馈异步发电机的定子绕组与电网直接相连,转子绕组通过一个带有电流控制环的背靠背电压源换流器(VSC)与电网相连。这样转子的电气频率就与机械频率解耦。换流器通过注入频率可变的转子电流来补偿机械频率与电气频率之差,如下式所示:
fs=pfm±fi
(12)
其中:fs为定子输出频率;p为发电机极对数;fm转子机械频率;fi为转子电流频率。通过控制转子的电流频率fi使得定子的输出频率fs保持恒定,从而实现风机的变速运行。其结构图如图2所示。

图2 双馈风机的基本结构
与恒速机组相比,双馈机组增加了转速控制模块、电压控制模块及桨距角控制模块。风速模块与恒速机组相同,减少了轴系模块。双馈机组的机械部分与电气部分基本上被换流器解耦,换流器的控制方式决定了轴系模型所反映的机端特性。由于换流器的动态过程相比于发电机电磁暂态过程要快得多,因此换流器用一个理想电流源等效代替。电流按d和q轴分解为iqr与idr,分别用于控制转速模块与电压模块,用下述方程描述:
(13)
(14)

发电机的电磁转矩以及向电网输出的无功功率也分别由iqr与idr决定:
(15)
(16)
流过换流器转子电流的限制是通过设置有功和无功功率限制值实现的。换流器是短路故障时双馈机组中最敏感的部件,因此必须对转速模块与电压模块以限制,以避免暂态过电流的影响。方程如下所示
(17)
桨距角控制模型由如下微分方程表示:
(18)
其中:φ为桨距角起始改变设置点函数,桨距角控制只有在转速超过同步转速时才开始起作用;Tp为桨距角控制时间常数。
1.3 直驱风电机组模型
直驱永磁风电机组不含高速旋转的齿轮箱,减小了机组本身故障发生的概率;采用永磁技术,无需励磁绕组和直流电源,使得机组结构更为精简。与双馈变速风电机组相比,其结构上的发电机模块,换流器与保护系统模块以及电压控制模块与之有所区别,其他模块基本相同,其结构如图3所示。
直驱同步机组的换流器与定子绕组相连,因此描述换流器的电流源电流分别为iqs、ids与idc用于转速控制、无功控制及电压控制。控制方程为

图3 直驱同步风机的基本结构
(19)
由此决定的电磁转矩及无功功率为
(20)
其中Ψp表示永磁磁通量。保护系统对流过换流器的定子电流限制如下:
(21)
2 基于PSAT的风机模型对暂态仿真算例
根据以上理论分析,本文通过基于Matlab的电力系统分析程序PSAT建立了包含风机的39节点仿真模型算例。其网络示意图如图4所示。
风电机组对电力系统的影响是通过其与常规同步机组相互作用得以体现。
在仿真中风电场接入的位置非常重要,与其他同步机的电气联系不能太弱。因此,将风电机组与同步发电机并联接在32节点处,类似风火捆绑式系统。其他发电机组采用5阶模型,计及自动励磁调节器和调速器的模型。发电机组发出的有功功率总计6194.5 MW,负荷吸收的有功功率总计6150 MW,风电机组发出的有功功率总计200 MW,与风电机组并联的同步机组发出功率450 MW,此系统的风电穿透功率为3.25%,即风电机组发出的有功功率与负荷吸收的有功功率比值。根据研究对象的不同,分别接入不同类型的风电机组,其模型由100台额定功率为2 MW的机组等值。

图4 39节点网络
3 分析与讨论
3.1 不同类型机组的暂态稳定性差异
在如上相同的网络结构基础上,分别考察三种风电机组故障情况下各机组本身的暂态稳定性,及其对系统暂态稳定性影响。三相故障是考察机组故障穿越能力的最坏工况,因此在13节点处设置一个1 s时发生的三相短路故障,故障持续时间分别设置为100 ms,230 ms,350 ms。在可接受的电压和频率水平下,从暂态稳定性方面对比三种机组的故障穿越能力。当故障持续时间为100 ms时各机组都能保持稳定,其中恒速机组的转速如图5所示,故障后在2.8 s时回稳。同步发电机1~9号机组与平衡机组5之间的功角差如图6所示,经过振荡逐渐回稳。对双馈机组与直驱机组,动态稳定主要考察他们的转子电流是否在式(17)与式(21)范围内,见图7。可知,两种机组均能保持动态稳定,且与之并联的同步机组也能保持暂态功角稳定。
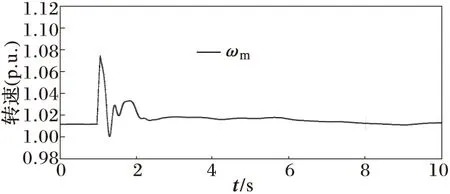
图5 故障切除时间为100 ms时恒速机组的转速

图6 故障切除时间为100 ms时各机组与平衡机组功角差

图7 转子电流Idr
当故障切除时间为230 ms时,32节点处的同步发电机失稳,与之并联的风电机组情况如下:恒速机组失稳,转速振荡转速如图8所示。双馈机组电流不越限,能保持稳定,如图9。直驱机组电流不越限,也能保持稳定。
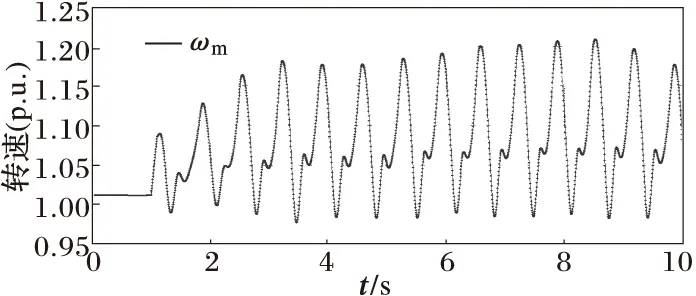
图8 故障切除时间为230 ms时恒速机组的转速

图9 转子电流Iqr
当故障切除时间为350 ms时,恒速机组过速,变速机组转子电流越限,且系统功角失稳如图10所示。对三种风电机组本身及其对系统的暂态稳定性对比如表1所示。
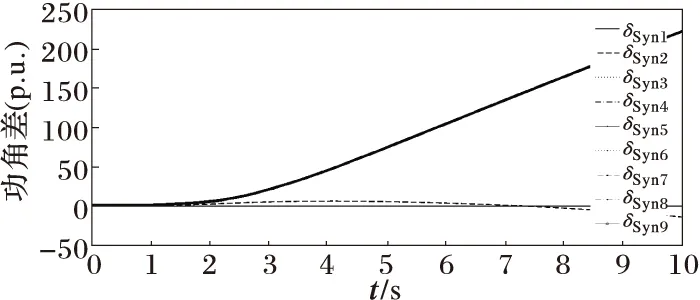
图10 故障切除时间为350 ms时各机组与平衡机组功角差

表1 三种风电机组及其系统稳定性对比
由上述分析可知,对于恒速异步风电机组,由于其机电耦合紧密,所以动态稳定性受发电机临界转速及故障持续时间的影响很大,而对于双馈机组和直驱机组,由于有换流器的作用,其动态稳定性主要取决于流过换流器电流的大小。该限制电流与换流器本身的特性密切相关。本仿真系统中是通过设定式(17)与式(21)的有功无功极限值来确定限制电流值。同步机组功角稳定方面,故障发生后,同步机组失稳常伴随着与之联系紧密的恒速机组失稳,而双馈机组与直驱机组受的影响较小。从上述仿真结果来看,直驱机组系统与双馈机组系统的暂态稳定性要好于恒速机组系统。另外,机组本身的动态稳定性也取决于变速机组换流器的特性,恒速机组的发电机参数和轴系模型参数等因素。
3.2 发电机参数对暂态稳定性的影响
装有常规感应发电机的恒速风电机组的电气、机械参数及可控性会影响其短时电压稳定性及故障穿越能力。感应发电机的转速与其暂态稳定性密切相关。由文献[13~15]知,轴系模型参数轴刚度KS对机组动态稳定性影响较大,越小的轴刚度易使发电机转子故障时获得越大的加速度。从而减弱恒速机组的暂态稳定性。由于风电机组的电气转矩与发电机参数相关,因此发电机参数也会影响恒速机组的暂态稳定性。下面考察发电机参数Rr、Rs、Xm、Xs和Xr的改变对恒速机组暂态稳定性的影响。系统发生三相故障,持续时间为200 ms时,发电机参数改变对恒速机组暂态稳定性的影响如图11至图15所示。
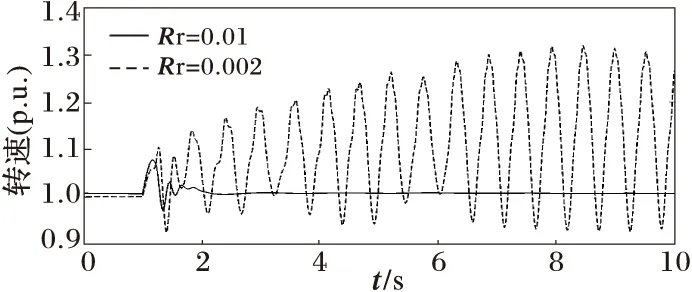
图11 Rr减小时恒速机组的转速
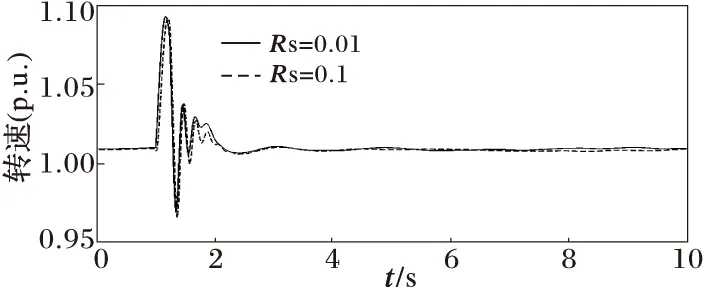
图12 Rs增大时恒速机组的转速

图13 Xs增大时恒速机组的转速
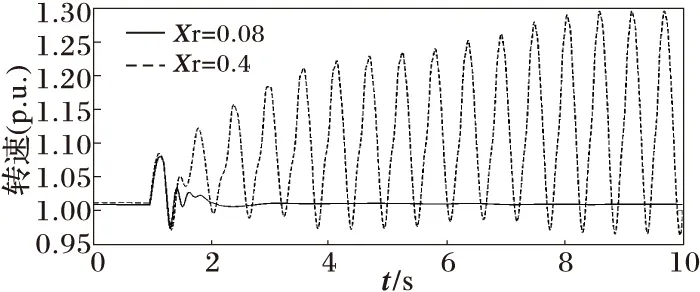
图14 Xr增大时恒速机组的转速

图15 Xm增大时恒速机组的转速
可见转子电阻Rr的增大,Xr和Xs的减小有利于恒速风电机组的暂态稳定性。而Xm和Rs对机组的暂态稳定性的影响不大。
4 结语
(1)恒速风电机组的暂态稳定性受发电机参数Rr、Xr、Xs和轴系参数的影响很大,Xs、Xr越小,Rr越大,越有利于恒速风电机组暂态稳定性的提高。Xm、Rs对机组暂态稳定性的影响不明显。
(2)双馈变速与直驱同步风电机组由于换流器的解耦作用,动态稳定性与发电机的转速关系不大,而主要是受换流器限制电流的影响。因此变速风电机组的动态稳定性与其换流器的特性密切相关。
(3)与风电机组电气联系紧密的同步机组稳定性对恒速机组的稳定性关联影响最大。直驱机组系统与双馈机组系统的暂态稳定性要好于恒速机组系统。
[1] 李欣然,惠金花,钱军,等(Li Xinran, Hui Jinhua, Qian Jun,etal).风力发电对配电网侧负荷建模的影响(Impact of wind power generation on load modeling in distribution network)[J].电力系统自动化(Automation of Electric Power Systems),2009,33(13):89-94.
[2] 雷亚洲,王伟胜,印永华,等(Lei Yazhou,Wang Weisheng,Yin Yonghua,etal).基于机会约束规划的风电穿透功率极限计算(Wind power penetration limit calculation based on chance constrained programming)[J].中国电机工程学报(Proceedings of the CSEE),2002,22(5):32-35.
[3] 迟永宁,刘燕华,王伟胜,等(Chi Yongning, Liu Yanhua, Wang Weisheng,etal).风电接入对电力系统的影响(Study on impact of wind power integration on power system)[J].电网技术(Power System Technology),2007,31(3):77-81.
[4] 吴俊玲,周双喜,孙建锋,等(Wu Junling, Zhou Shuangxi, Sun Jianfeng,etal).并网风力发电场的最大注入功率分析(Analysis on maximum power injection of wind farm connected to power system)[J].电网技术(Power System Technology),2004,28(20):28-32.
[5] 曹娜,李岩春,赵海翔,等(Cao Na, Li Yanchun, Zhao Haixiang,etal).不同风电机组对电网暂态稳定性的影响(Comparison of effect of different wind turbines on power grid transient stability)[J].电网技术(Power System Technology),2007,31(9):53-57.
[6] 张红光,张粒子,陈树勇,等(Zhang Hongguang, Zhang Lizi, Chen Shuyong,etal).大容量风电场接入电网的暂态稳定特性和调度对策研究(Studies on the transient behavior and dispatching strategy of power system integrated with large scale wind farms)[J].中国电机工程学报(Proceedings of the CSEE),2007,27(31):45-51.
[7] Li H, Chen Z. Overview of different wind generator systems and their comparisons[J].IET Renewable Power Generation,2008,2(2):123-138.
[8] 石立宝,戴世强,徐政,等(Shi Libao, Dai Shiqiang, Xu Zheng,etal).大规模双馈型风电场并网的系统暂态稳定仿真(Transient stability simulation with large scale grid-connected wind farms of DFIG type)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2009,21(4):1-7.
[9] 申洪,梁军,戴慧珠(Shen Hong, Liang Jun, Dai Huizhu).基于电力系统暂态稳定分析的风电场穿透功率极限计算(Calculation of wind farm penetration based on power system transient stability analysis)[J].电网技术(Power System Technology),2002,26(8):8-11.
[10]Slootweg J G, de Haan S W H, Polinder H,etal. General model for representing variable speed wind turbines in power system dynamics simulations[J].IEEE Trans on Power Systems, 2003,18(1):144-151.
[11]Milano F. An open source power system analysis toolbox[J]. IEEE Trans on Power Systems,2005,20(3):1199-1206.
[12]倪以信,陈寿孙,张宝霖,等.动态电力系统的理论和分析[M].北京:清华大学出版社,2002.
[13]Akhmatov V.风力发电用感应发电机[M].北京:中国电力出版社,2009.
[14]Thomas A. Wind Power in Power Systems[M].Stockholm:John Wiley amp; Sons,2005.
[15]Pabol L. Doubly fed induction generator model for transient stability analysis[J].IEEE Trans on Energy Conversion,2005,20(2):388-397.
郝元钊(1984-),男,硕士研究生,研究方向为电力系统分析与控制。Email:haoyuanzhao@126.com
李培强(1975-),男,工学博士,副教授,硕士生导师,主要从事电力系统分析与控制的研究和教学工作。Email:lpqcs@hotmail.com
李欣然(1957-),男,工学博士,教授,博士生导师,系主任,主要从事电力系统分析与控制及负荷建模的教学和研究工作。Email:lixr1013@yahoo.com.cn
AnalysingtheImpactofWindPlantonPowerSystemTransientStability
HAO Yuan-zhao, LI Pei-qiang, LI Xin-ran, BI Zheng-jun, WANG Ling
(College of Electrical and Information Engineering, Hunan University,Changsha 410082, China)
As the most environmental friendly source of power generation,wind power turbines are expanding in the grid. It will also have a broad and deep impact on power system stability. In this paper, a comparison of reduced-order models is made among three mainly used wind turbines which are constant speed wind turbine(CSWT),doubly fed induction generator(DFIG) and direct drive synchronous generator(DDSG). Then a MATLAB-based power system analysis toolbox (PSAT) is used for investigating the dynamic behavior of three generators in different fault clearing time. At last, the impact of wind turbine parameters on the wind turbine stability is discussed. A conclusion is drawn that with the increase ofRrand decrease ofXr,Xsis benefit to the transient stability.
power system analysis toolbox(PSAT); wind turbines; generator parameters; transient stability
TM712
A
1003-8930(2012)02-0041-06
2011-05-06;
2011-10-12
国家自然科学基金项目(50977023);中国博士后科学基金项目(20100471211);湖南省自然科学基金项目(10JJ9023),(10JJ2043)

