热应力及外压影响下长输管道固定墩推力有限元计算分析

李茂华，高剑锋，安佰燕

霍锦宏，王 进(中国石油天然气管道工程有限公司，河北 廊坊 065000)

热应力及外压影响下长输管道固定墩推力有限元计算分析

李茂华，高剑锋，安佰燕

霍锦宏，王 进(中国石油天然气管道工程有限公司，河北 廊坊 065000)

建立固定墩附近直管线热应力及结构力学模型，根据西气东输二线的现场资料，应用Ansys有限元分析软件，计算管道在上覆压力、管道内输气压力及管线内温度作用，管线在固定墩处的应力及应变的大小，分析热应力及外压管线应力及固定墩推力的大小分布。结果表明，管道在地层均匀地应力变化不大及管道正常输送油气时，外挤载荷作用对管线的应力影响较小；管线内温度变化时，造成管线产生了较大的热应力及并在固定墩处产生较大的推力；在弯头附近直管应布置固定墩外，在直管段可以按照一定的距离布置固定墩，以减小管线局部集中应力及轴向变形位移。

热应力；管道应力；有限元；弹性模量；抗压强度

西气东输二线长输管线为天然气输气管线，由于输送距离长，管道内气体温度随管道的长度增加会发生变化，造成管道温度分布极不均匀。由于在输气过程中，热量在管线及地层中的损耗，管道内外壁的温度不同，造成管道局部产生热应力及热胀冷缩效应产生的应变[1]。为此，笔者根据西二线管线的实际资料，利用有限元法建立了平面力学及热应力分析模型，计算分析了管线的应力大小及轴向变形位移，以期得到全面的认识。

1 数值计算模型

长输管线在生产中，当地层均匀地应力变化不大时，管道主要受到上部砂石土层的压应力，管道自重产生的压力，管线内部输气压力及气体温度变化产生的热应力作用。由于管道输送距离大，在外力及温度的影响中，管道应力分布较不均匀，应变随之不均匀分布，在轴向上产生的变形位移会随管道长度增加而增大，由此产生较大的轴向应力挤压土层造成管线发生变形和位移。计算模型应该较为真实的反映出非均匀地应力及温度效应作用对管线应力及变形的影响，笔者应用平面应力应变及轴对称理论[2]，通过建立管线外压和温度作用的力学模型，利用Ansys有限元软件分析管线的应力分布和变形大小，以期得出结合管道运营和工程建设的结论保证管线长期有效生产。

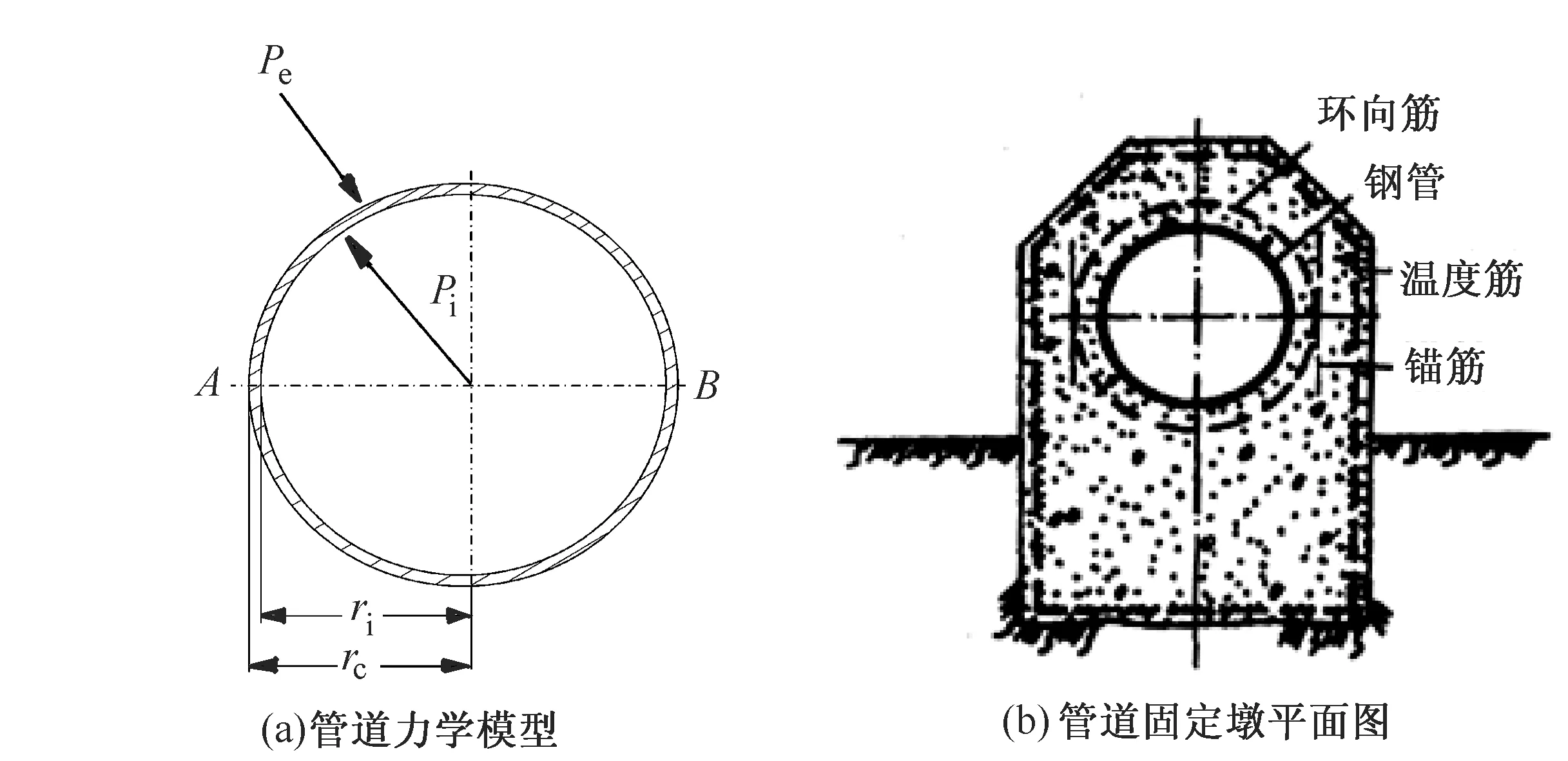
Pi：管线内压；Pe：管线外压； ri：油气管线内径；rc：油气管线外径

1.1数学模型

根据弹性力学理论[3]，输气管线在地层中受到的外挤载荷和热应力可以转化为平面应力及轴对称问题，如图1(a)所示。图1(b)为管道固定墩平面图。由于固定墩的作用，输气中管道生应力大部分集中于固定墩和管道外壁的接触面上。

为分析输气管线受力变形，对管线外压及热应力系统采取如下假设：管道厚度沿环向和长度分布均匀并稳定；管道内气体温度均匀传导在管线内壁；管线材料为各向同性的均匀弹性体，忽略外防腐层对管道应力的影响。输气管线受力及热效应变形属于平面对称问题[4]，管线在径向和轴向应力分布不均产生变形，因此可采用半平面分析油气管线热效应应力系统。平面问题应力-应变关系为：

{σ}=[D]{ε}=[D][B]{q}e

(1)

式中，[D]为弹性矩阵,MPa；{ε}为弹性应变，%；[B]为应变矩阵,%；{q}e为单元节点位移列阵，m。

根据虚位移原理[5-6]，可以将实际荷载作用下杆件的位移及各微元2端横截面间的变形位移作为虚位移。要确定在实际荷载作用下杆件上某一截面沿某一指定方向(或转向)的位移Δ，可以在该点处施加一个相应的单位力，并将它看作荷载，由单位力所引起的杆件任意横截面上的内力分别记为G、M、Q、T，由于温度均匀传导，杆件内的等效热载荷记为He，因此杆件的虚位移原理表达式为：

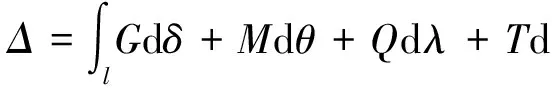
(2)

式中，{He}=∬s[B]T[D]{ε}dxdy；{ε}为弹性应变，%；s为单位微元面积，m2。

根据弹性体受力变形的虚位移原理[7]，可得到所有节点的有限元方程：

[K]{q}={R}

(3)

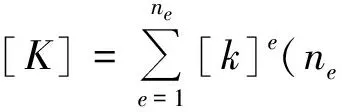
1.2有限元模型

管线在空间是Z轴对称轴的圆柱体，在径向是Y轴对称轴的平面圆环。根据有限元平面应力及轴对称理论[8]，管道受力及热效应载荷可以建立平面应力及轴对称模型[9-11]。应用西气东输二线管道施工及运行的参数，建立平面有限元模型。具体参数如表1。有限元模型采用二维实体，对模型采用映射网格划分单元。单元类型选择8节点热应力及结构应力实体单元。

表1 计算模型的材料参数

根据弹性力学和有限元理论，管线热应力和外挤载荷的空间问题可以应用平面应力及轴对称建立平面有限元模型，计算分析管线的应力分布及大小,如图2所示。图2(a)为1219mm外径X80管线空间力学模型;图2(b)为X80管线三维剖面，以Z轴为对称轴；图2(c)为管线旋转截面，以Z轴为对称轴旋转，为管线空间模型。

为较好的计算分析管线内压外挤载荷及热应力作用下，应力应变分布及变形大小，管线旋转截面以X轴方向为径向，Y轴为旋转对称轴，应用Ansys有限元软件建立平面轴对称模型，分析外挤载荷内压及热应力对管线的应力影响和应变大小。对模型采用映射网格划分，如图3所示。X轴为管道厚道，取d=22mm，Y轴为管道轴向长度，取l=350mm。模型在X轴约束Y方向位移，模型内壁为气体压力，根据西二线资料，取Pi=8～12MPa。管道内气体温度T=10～50℃，温度均匀传导在管道壁并均匀分布。外压Pe如图1所示，AB线上部受到土层压应力作用，AB线以下为土层及管道重量的压力，Pe在管线外壁不均匀分布。

2 外挤载荷及热效应载荷作用下管线的应力分布及应变大小

地层均匀地应力变化不大的条件下，管线受到上覆土层压力、内部气体压力及温度作用。由于管道外壁防腐层不具有保温作用，管道内壁和外壁温度不同，外壁接触地层温度部分传导入地层并损耗，外壁较内壁温度低。管道埋设在冻土层以下，气候条件的变化会造成地层和管道外壁热传导效应的变化，管道外壁较内壁温度差会增加。因此，在内外壁不同温度及外压作用下，管道的应力大小分布会产生较大的变化。图4所示为管道在不考虑内外压作用下温度及应力应变大小分布。

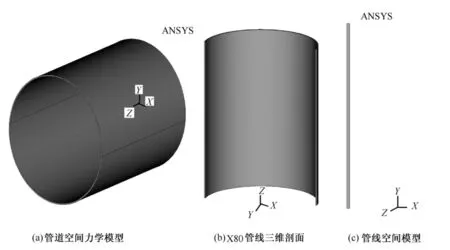
图2 管线空间力学模型及平面轴对称模型

图3 映射网格划分

图4 无内外压作用条件下管道温度和应力大小分布

由计算可知，在y=0处有固定墩约束轴向位移，管道无内外压作用，在生产中管道外壁热量损耗，较内壁温差不大时，如图4(a)所示，管道内壁温度为气体温度50℃，热量由内壁均匀传导外壁，温差为5℃。在较小温差影响下由热应力模型计算得到管线应力大小及分布，如图4(b)所示。管道最大应力在内壁产生，达到了8MPa，由于一端有固定墩约束位移，管线应力可由轴向伸长补偿得到减小，轴向伸长量为0.018mm，由分析可知，管线在温度影响下，最大热应力在内壁产生，轴向产生较大的位移。在无温度损耗影响下，管线应力大小及分布如图4(c)所示，管道内外壁温度为50℃。在底部固定墩的约束下，管线应力分布极不均匀，最大应力小于1MPa，轴向伸长量达到0.0193mm。这是由于温度产生的热胀冷缩效应，对管线造成了较大的轴向应力，轴向的伸长补偿了应力集中分布。因此，温度在管道轴向产生了较大的应力，此时固定墩起到了最大限度减小管道轴向变形的作用，但管道所产生的推力集中作用到了固定墩上，管道在固定墩产生的应力为固定墩所受的推力。

管线生产中，根据西二线管线内压力及上覆土层压力计算分析，内压为Pi=8～12MPa，外压Pe=Ps+Pg，其中，Ps上覆土层压应力；Pg为管线自重产生的压应力，管线埋设深度为3～5m，由砂土密度和钢管密度计算可知Pelt;1MPa，Pe在管线外壁非均匀分布，且远小于管线的屈服强度。因此，在管线生产中，地应力不发生较大变化时，可以忽略外压对管线应力造成的影响。因此，影响管线应力大小及分布的主要因素为内压和温度效应，如图5所示，管道一端有固定墩约束位移，管道内压Pi=8MPa，管道内气体温度为45℃，外壁热量损耗，外壁温度为42℃。

由分析可知，在内压和温度影响下，最大应力为50MPa，在管道内壁产生，如图5(a)所示，较无内压管道应力大。由于管线一端无固定墩，管线沿轴向伸长，最大位移0.0162mm在远离底部固定墩位置产生，如图5(b)所示。管道两端有固定墩时，应力为111MPa，远高于一端有固定墩应力，固定墩承受了较大的推力。

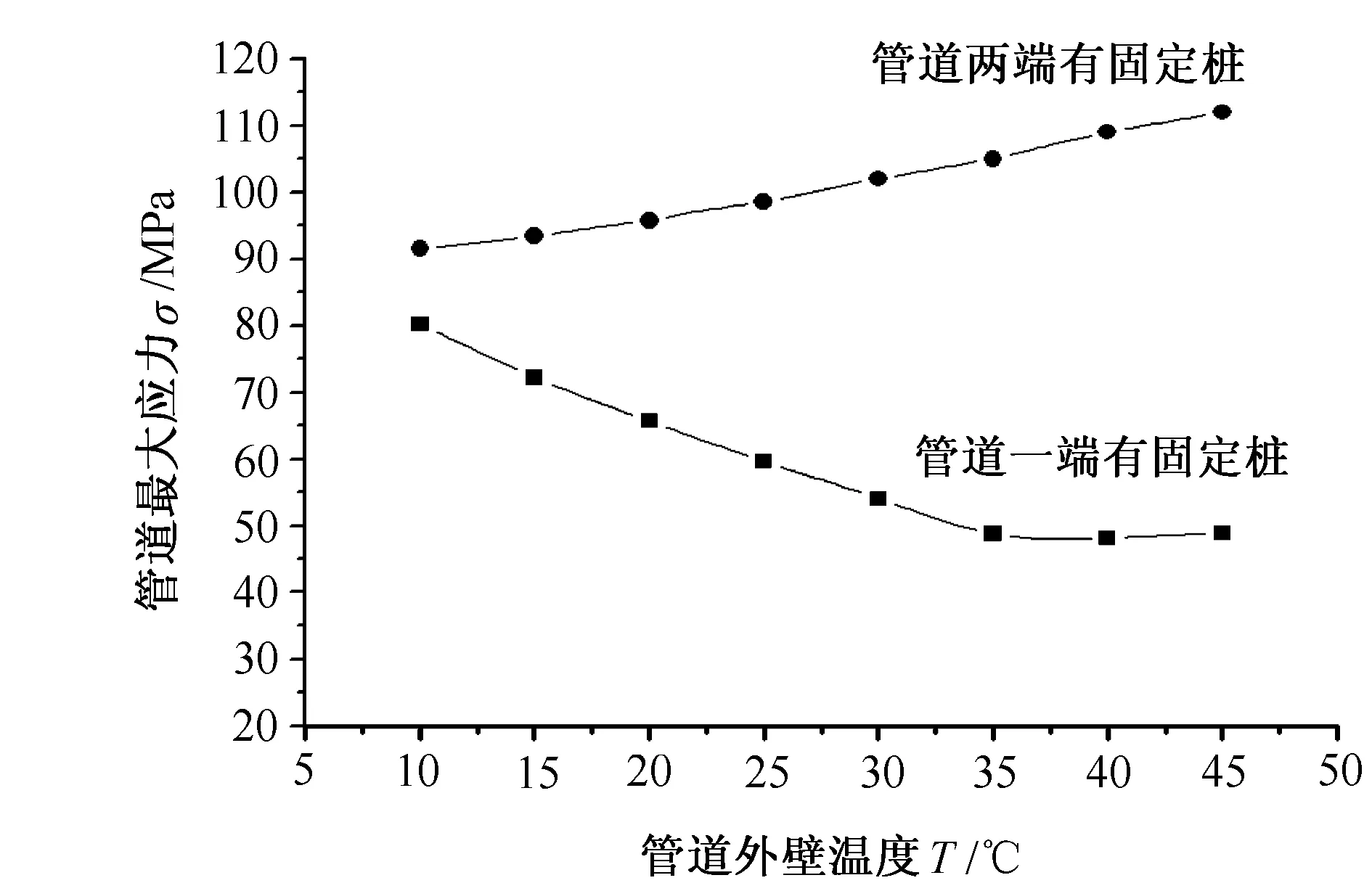
图6 有无固定墩在内外壁温度影响下管线应力计算结果

下面分析固定墩及温度变化对管线应力大小及分布的影响，建立管道在温度变化时应力模型。取管道内气体压力Pi=8MPa，内壁温度T=45℃，管道外壁温度10～45℃。管线为一端有固定墩和两端有固定墩约束计算模型，如图6所示，管道内外壁温差对管线应力大小的影响。由计算结果可知，管道两端有固定墩较一端有固定墩应力大，且随着温差的增加，两端固定墩管道应力产生的推力约为一端固定墩的2倍。由于模型的长度为350mm，在温度变化中为拟合管道随长度的增加，固定墩推力的大小及变形位移的大小。

根据西二线的资料，取管道内气体压力Pi=10MPa，内壁温度T=10～45℃，管道外壁温度T0=8～40℃。分析计算管道随长度增加应力的大小及固定墩推力大小，如图7所示。内外壁温差保持在2～5℃。由计算结果可知，当内壁温度为35℃，外壁温度为30℃，随着管道长度的增加，两端固定桩承受的推力随着管道应力的增加而增大，由管道应力曲线拟合得到管道长度L和固定墩推力大小计算结果为每米增加0.12MPa。管道每增加1km，固定墩受到的推力增加约120MPa压力。因此，固定墩应按照距离和应力的拟合关系，选择合理的埋设间距，保证经济上的可行和减小管道局部应力和轴向变形位移。

在内外壁温差接近保持2～5℃时，管道轴向位移随模型的长度变化如图8所示。取气体压力Pi=10MPa，内壁温度T=20～35℃，管道外壁温度T0=15～30℃。计算分析不同温度管道轴向变形大小。由分析可知，管道轴向变形位移随管道内气体温度的增加而增大。长度相同的管道，管道温度越高，轴向位移越大。因此，固定墩受到的推力越大。管道气体压力对管道径向压力影响较大，表现为管道内壁应力随径向的增加而减小，外壁应力小于内壁应力。固定墩与管道外壁接触，因此，外壁的压应力作用于固定墩内壁，由于固定墩减小管道轴向变形位移，受到了较大的推力，为减小随着管道的长度增加而增大的变形位移，可以采用合适的温度，减小管道热胀冷缩效应产生的轴向变形。

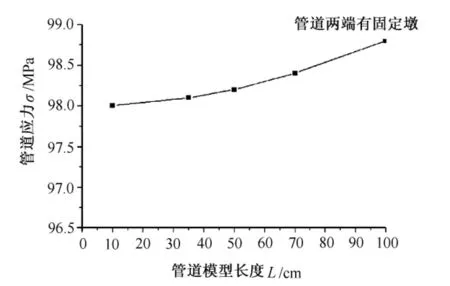
图7 两端有固定墩约束管道不同长度下应力计算结果

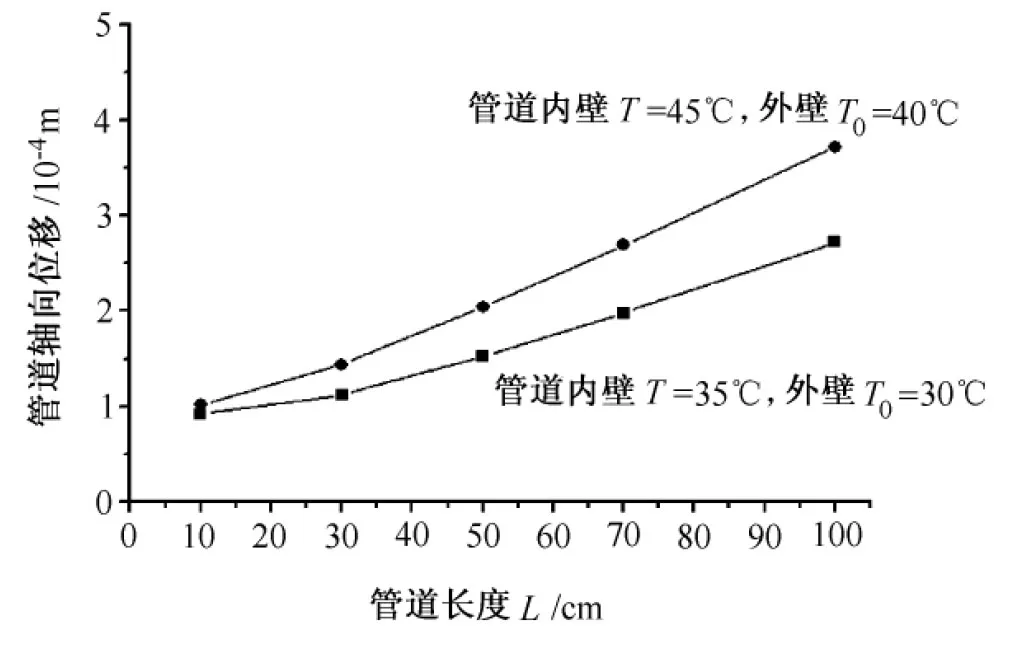
图8 不同温度管道轴向位移计算结果

3 结 论

1)地层均匀地应力变化不大时，外压对管道应力影响较小。内压和温度造成管道产生较大应力。管道气体压力对管道径向压力影响较大，表现为管道内壁应力随径向的增加而减小，外壁应力小于内壁应力。

2)在内壁相同和外壁接近时，两端有固定墩较一端有固定墩管道应力大，应力为一端固定管道的约2倍。由管道应力曲线拟合得到管道长度L和固定墩推力大小计算结果，管道每增加一公里，固定墩受到的推力增加约120MPa压力。因此，固定墩布置应按照距离和应力的拟合关系，选择合理的埋设间距，保证经济上的可行和减小管道局部应力和轴向变形位移。

3)在输气温度的影响中，为减小随着管道的长度增加而增大的轴向位移，可以采用合适的温度，以减小管道热胀冷缩效应产生的轴向变形和管道应力。

[1]Oleary P M，Datya S K.Dynamics of buried pipelines[J].Soil Dynamics and Earthquake Engineering，1985，4(3)：151-154.

[2] Hobbs R E.Pipeline bucking caused by axial loads[J].Journal of constructional Steel Research，1981，1(2)：4-8.

[3] 程昌钧,朱媛媛.弹性力学[M] .上海：上海大学出版社，2005.

[4] 王致祥.管道应力分析与计算[M].北京：水利电力出版社，1983.

[5] 孙训方，方孝淑，关来泰.材料力学[M].北京：高等教育出版社，1982：234-248.

[6] 罗维东.有限变形弹性体的广义虚功原理[J].石油大学学报(自然科学版)，1999,23(5)：60-62.

[7] 张立松.闫相祯.杨秀娟.水平隧道管道固定墩推力虚功原理解答及应用[J].中国石油大学学报(自然科学版)，2010(3):32-35.

[8] 杜平安，甘娥忠，于亚亭.有限元法原理、建模及应用[M].北京：国防工业出版社，2004：35-42.

[9] 冯继蓓，孙蕾.安定性分析在热力管道设计中的应用[J].特种结构，2007(3)：58-60.

[10] 李坚.管道应力分析及柔性设计[J].炼油技术与工程，2010，40(1)：62-64.

[11] 张立松，闫相祯，杨秀娟.长输油气管道强度与优化设计软件[J].油气储运，2009(12):252-253.

[编辑] 洪云飞

10.3969/j.issn.1673-1409(N).2012.03.024

TE973

A

1673-1409(2012)03-N071-04

2012-01-16

中石油西气东输二线工程项目(HGPE201129306)。

李茂华(1980-)，男，2004年大学毕业，硕士，工程师，主要从事地层应力、管道工程应力设计方面的研究工作。