主成分分析法改进贝叶斯网络入侵检测

文/李静 冯祖洪

主成分分析法改进贝叶斯网络入侵检测

文/李静 冯祖洪

使用主成分分析的方法对数据集进行降维，将滑动窗口引入到贝叶斯网络分类算法中，从而得到改进的贝叶斯网络分类算法。实验证明，改进的算法能够有效地降低分类数据的维数，同时该算法建立的入侵检测模型能够更好地检测出已知的入侵攻击类型。

当今在全球范围内，对计算机及网络基础设施的攻击已经成为一个越来越严重的问题，与此同时，入侵检测技术也成为人们日益关注的研究课题之一[1]。从当前的一些研究成果来看，已有的一些检测技术对于已知的入侵行为检测精度高，误报率较低，但对于未知攻击的入侵模式的检测率和误报率的结果均不太理想，而且在时效性方面也不能令人满意。因此如何建立具有较强的有效性、自适应性和可扩展性的入侵检测模型成为入侵检测领域中重要的研究课题[2]。

由于贝叶斯网络具有坚实的数学理论基础以及综合先验信息和样本信息的能力，近年来已成为入侵检测模式分类的研究热点之一。但是，基于贝叶斯网络的入侵检测技术在对数据进行检测时存在两个问题：其一[3]是贝叶斯网络结构节点太多，分类过程中的计算量呈指数增长，导致分类效率较低；其二是在检测的过程中没有考虑到当前的攻击行为和安全状态，仅仅是根据原始训练数据集生成的固定不变的贝叶斯网络来进行测试，对检测的精度造成一定的影响。

对于上述第一个问题，本文提出基于主成分分析的特征提取方法。利用主成分分析的降维思想，减少训练数据的变量，进而简化贝叶斯网络。对于第二个问题，本文提出滑动窗口机制。该机制将窗口中的数据设为训练数据集，具体解释如下：首先将测试数据集追加到训练数据集的尾部，初始窗口为原始训练数据集，每当检测完N条测试数据时，将滑动窗口向下移动N条数据（窗口大小保持不变），这样就可以得到一个不断更新的训练数据集。由此，训练得到的贝叶斯网络就包含系统当前的安全信息。实验证明，本文提出的方法可以有效地提高分类效率和检测精度。

主成分分析

主成分分析也称主分量分析，利用降维的思想，把多指标转化为少数几个综合指标[4]。

主成分算法的实现如下[5]：

1. 对训练集矩阵进行标准化处理，

得到矩阵

其中，

2. 求相关矩阵

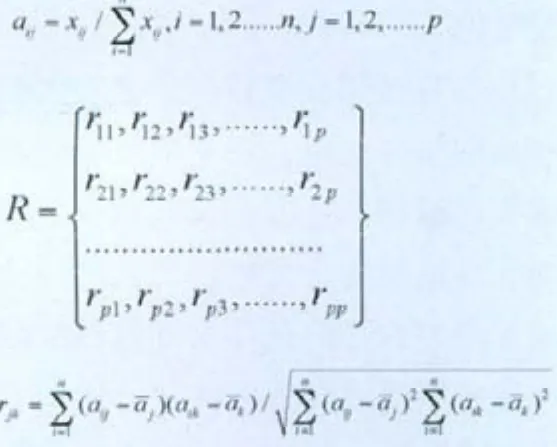
3. 求R矩阵的特征值和特征向量

由于R是一个对称矩阵，所以在计算中只要对R的上三角矩阵求特征值和特征向量即可。

4. 求出主成分

将求出的特征值按大小依次排列，便得，

原则确定m，并依次排列特征向量，

就可得到我们所需的主成分。

贝叶斯网络

贝叶斯网络是一个功能强大的知识表示和不确定条件下的推理工具，由一个有向无环图及图中各个节点所附加的一张概率表组成[6]。其中，有向无环图的各个节点表示领域中不同的变量，节点之间的弧表示变量之间的依赖关系。根节点X所附的是它的边缘分布P(X)，而非根节点X所附的是条件概率分布P(X|π(X))，其中π(X)代表X的父节点。简单地讲，有向无环图从定性的层面描述变量之间的依赖独立关系，而概率分布从定量的层面刻画变量对其父节点的依赖关系。为方便描述，文章中将有向无环图称作贝叶斯网络结构，将各个节点的概率表称作节点参数。

改进贝叶斯网络入侵检测

利用主成分分析改进贝叶斯分类算法

从理论上分析，由于贝叶斯网络具有坚实的数学理论基础以及综合先验信息和样本信息的能力，因此比其他分类算法，如朴素贝叶斯、支持向量机等，具有更好的分类精度。但是，已有的贝叶斯网络算法在对训练数据进行训练时，并没有考虑到大量冗余的数据属性会提高数据的维数，增加分类计算量，造成分类效率的下降。基于这样的情况，本文提出在利用训练数据集进行训练之前，首先对训练数据集进行特征选择或者特征提取。常用的特征选择方法主要有信息增益、信息增益比、距离度量等。虽然采用这些特征选择算法会大幅度减少计算量，但是由于忽略一部分属性对分类所起的作用，导致分类精确度不够理想。文本采用主成分分析的方法对特征属性进行特征提取，这样不仅可以大大地减少数据维数，减少计算量，同时也可以最大限度地利用原数据的分类信息，使得分类精度相对较高。

例如，某数据集有特征属性A1、A2、A3、A4、A5、A6、A7，对分类所起的作用分别为：0.2324、0.208、0.1753、0.1052、0.1038、0.08931、0.0859在通过特征选择后得到对分类所起作用较大的前四个属性A1、A2、A3、A4对分类所起的作用之和为0.7209。而在用主成分分析之后得到的结果可能是X1、X2、X3、X4，而根据主成分分析算法，得到的这四个主成分对分类所起的作用之和一定大于0.85。相比之下，本文选择主成分分析的方法对训练数据集进行特征提取来减少特征属性，从而减少计算量，提高检测效率。

改进贝叶斯分类算法的步骤

设训练数据集为M0，改进贝叶斯分类算法的步骤分别是：

1. 对训练数据集M0进行预处理（如：数值化处理和离散化处理）得到训练数据集M1。

2. 采用之前提到的主成分分析方法对M1进行主成分分析，得到包含较少属性的新数据集M2。

3. 对数据集M2进行离散化处理得到新的数据集M 3。

4. 参照基于互信息的贝叶斯网络结构生成算法[7]，对M3进行训练得到贝叶斯网络的结构。

5. 利用滑动窗口机制，对测试集中的数据进行测试。具体步骤如下：

（1）对训练数据集设置两个指针，分别为头指针P1(指向训练数据集的首部)和尾指针P2（指向训练数据集的尾部）；同时，对测试数据集设置两个指针，分别为头指针Q1(指向测试数据集的首部)和尾指针 Q2（指向训练数据集的尾部），即P=P1，Q=Q1；

（2）把指针P所指向的数据存入数据集M中，P=P+1；

（3）重复（1），直到P>P2；

（4）通过数据集M计算贝叶斯网络结构各个节点的参数C（即概率表）；

（5）用贝叶斯网络结构和参数C对训练数据集中指针Q所指向的数据进行测试，并将该条数据追加到训练数据集M的尾部，P2=P2+1，Q=Q+1；

（6）重复（4）的操作，直到Q=Q1+N或者Q>Q2；

（7）如果Q>Q2，继续执行下一步；否则，P 1=P 1+N，P=P 1，转到（1）；

（8）测试完毕，计算正确率。

试验及分析

评估指标

本实验采用F1测试值作为试验评估指标。F1测试值的具体计算公式如下[8]：

其中，

实验设计及结果

本实验采用的数据来自KDDCUP1999数据集。该数据集作为入侵检测领域中的权威数据，是在军事网络环境中运用非常广泛的模拟入侵攻击试验得到的。该数据集包含490万条数据，每条数据就是一个网络连接记录。其中，每条记录由41个特征属性和第42个用来标记该记录是正常数据还是某种攻击类别的属性组成[9]。该数据集包含的四大攻击类[10]分别是：DoS(Denial-of-service)，拒绝服务攻击；R2L(Unauthorized access from a remote machine to a local machine)，是来自于远程主机的未授权访问；U2R(Unauthorized access to local super user privileges by a local unprivileged us未er)授权的本地超级用户特权访问；Probing(surveillance and probing)端口监视或扫描。本文从该数据集中抽取12万条记录，其中50%作为训练集，剩余50%作为测试集。

通过对6万条训练数据进行分析，得知41个特征属性中的8个属性（is_hot_login，num_outbound_cmd，root_shell，land，su_attempted，urgent，num_shells，num_failed_logins）对分类几乎不起作用（其99%以上的属性值是相同的）。本实验对剩余的33个属性进行主成分分析，得到12个主成分，并对其离散化。

数据离散化后，将这12个主成分作为前12个变量，并将原训练数据集中的第42个属性（标记类别的属性）作为第13个变量组成新的训练数据。运用参考文献中的算法对新训练数据进行训练得到如图1所示的贝叶斯网络结构。计算得到网络节点参数，即变量的先验概率表或条件概率表。由于各个变量的取值较多，导致概率表庞大，文章中仅截取节点3和节点6的概率表，如表1、表2所示。

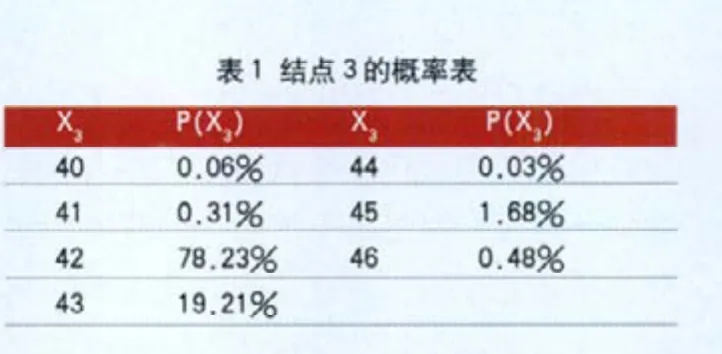
表1 结点3的概率表X3 X3P(X3)0.03%1.68%0.48%44 45 46 40 41 42 43 P(X3)0.06%0.31%78.23%19.21%

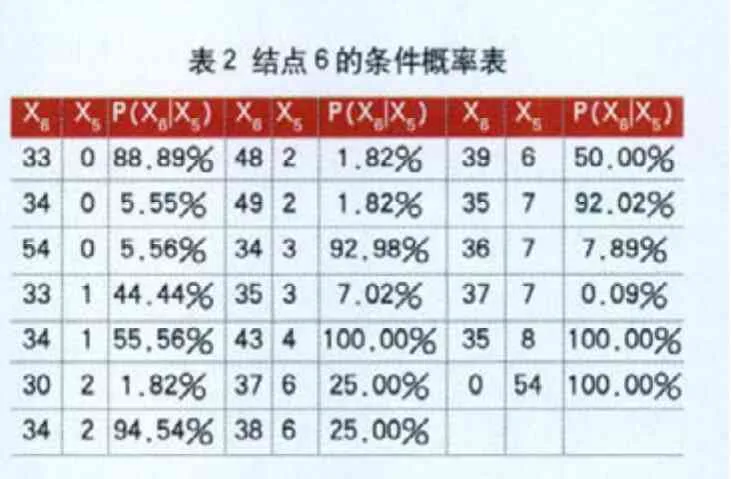
表2 结点6的条件概率表X6 X6 33 34 54 33 34 30 34 X50001122 P(X6|X5)88.89%5.55%5.56%44.44%55.56%1.82%94.54%X6 48 49 34 35 43 37 38 X52233466 P(X6|X5)1.82%1.82%92.98%7.02%100.00%25.00%25.00%39 35 36 37 35 0 X5677785 4 P(X6|X5)50.00%92.02%7.89%0.09%100.00%100.00%

表3 F1值对比算法记录类型(%)未加入滑动窗口的贝叶斯网络算法加入滑动窗口的贝叶斯网络算法Normal 92.46 93.7292.5681.3289.3690.21 Dos 90.29 Probing 79.86 R2L 87.58 U2R 88.96

贝叶斯网络生成之后，用已有的贝叶斯网络分类算法和基于滑动窗口的贝叶斯网络分类算法进行比较。通过多次试验证明，当滑动窗口的大小为1000时，分类效果较好。算法采用Matlab编程实现，并分别计算出两个不同算法的准确率和查全率。试验后得到两种不同算法针对每个类具体的F1值，如表3所示。

实验结论

1. 与直接用标准数据集中的数据训练贝叶斯网络相比较，用主成分分析方法对数据集进行特征提取会大大减少贝叶斯网络训练过程中的计算量；

2. 由表2可知，使用滑动窗口可以明显提高贝叶斯网络的检测精度。

本文在对KDD CUP 1999数据集进行分析的基础上，使用主成分分析的方法对数据集进行降维，将滑动窗口引入到贝叶斯网络分类算法中，从而得到改进的贝叶斯网络分类算法。试验证明，改进的算法能够有效地降低分类数据的维数，同时该算法建立的入侵检测模型能够更好地检测出已知的入侵攻击类型。但对于未知的攻击，检测效果还不是很理想，这也是本文下一步要考虑的问题。

扩展阅读：

[1]杨德刚.基于模糊C均值聚类的网络入侵检测算法.计算机科学,2005,32(1):86-91.

[3]李冰寒,高晓利,刘三阳,李战国.利用互信息学习贝叶斯网络结构[J].智能系统学报,2011,6(1):68-71.

[4]张尧庭等.多元统计分析引论[M].北京:科学出版社,1982.

[5]于涛.主成分分析及其算法[J].金筑大学学报,1996,22(2):75-78.

[6]张连文,郭海鹏.贝叶斯网引论[M].北京:科学出版社,2006.

[7]Jie Cheng,David A.Bell,Weiru Liu,et al.Learning belief networks from data: an information theory based approach[C]. In Proceedings of the Sixth ACM International Conference on Information and Knowledge Management,325-331.

[8]王卫玲,刘培玉,初建崇.一种改进的基于条件互信息的特征选择算法[J].计算机应用,2007,27(2):433-435.

[9]杨锋.基于数据挖掘的入侵检测技术研究[D].哈尔滨:哈尔滨工程大学,2006.

[10]王越,谭淑秋,刘亚辉.基于互信息的贝叶斯网络结构学习算法[J].计算机工程,2011,37(7):62-64.

（作者单位为北方民族大学计算机科学与工程学院）