一类人口发展系统生育率的双控制问题

蔡吉花，　丛凌博

(黑龙江科技学院 理学院, 哈尔滨 150027)



一类人口发展系统生育率的双控制问题

蔡吉花，丛凌博

(黑龙江科技学院 理学院, 哈尔滨 150027)

研究了一类时变人口发展系统，把非竞争生育率和竞争生育率作为双控制元讨论了一类时变人口发展系统最优控制问题。利用泛函分析方法，证明了时变人口发展系统优化控制元的存在性和唯一性。

人口发展系统; 生育率; 闭凸集; 双控制元

0引言

人口发展系统的研究历史悠久,从最初的常微分方程的人口模型——Malthus人口模型和考虑竞争的Logistic模型,发展到如今广泛使用的偏微分方程人口模型。在考虑竞争条件下,多个数学家提出并完善的人口发展系统:

(1)

偏微分方程人口模型形式的不同主要体现在妇女总和生育率β(r,t)的不同表示。文献[1]中对问题(1)的β(r,t)=β(r)时,利用算子半群理论得到解的唯一性和稳定性,为使我国人口趋于稳定,生育率控制在β≤2.16。文献[2-3]进一步发展了人口系统的渐进性和稳定性理论。文献[4]中首先提出了考虑竞争生育率的人口模型(1)。在文献[5]中用特征线法讨论了人口模型(1)的迭代解。关于人口系统问题(1)中生育率β(r,t)的最优控制问题,文献[6-8]分别研究了β(r,t)=β(r)、b(r)、c(r)作为控制元的人口系统的最优控制问题。以往的人口模型的最优控制问题都是以生育率的单个控制元作为研究对象,笔者将β(r,t)=b(r)-c(r)p(t)中的(b(r),c(r))作为双控制元函数,把人口模型的两个生育率作为控制对象,讨论了双最优控制元的存在性和唯一性。

记Ω=[0,rm]×[0,T],I=[0,rm],T是所考虑的最大时间范围,取t时刻人口的总数p(0)(t)=C,在Ω中式(1)成为如下问题:

(2)

利用特征线方法[5],可以得到在Ω中方程(2)的迭代解p(1)(r,t)。继续这个过程:

(3)

其迭代解为

(4)

文献[7]已经证明了问题(3)的迭代解{p(n)(r,t)}在Ω中收敛于p(r,t),p(r,t)称作方程(1)的极限解,表示为

1　基本概念

设L2(Ω)是Ω上Lebesgue平方可积函数构成的Hilbert空间,内积和范数分别定义为

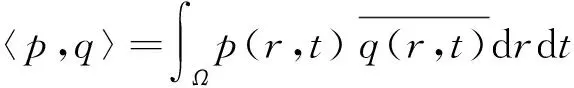
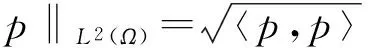
类似的设L2(I)表示Lebesgue平方可积函数构成的Hilbert空间,内积和范数分别定义为

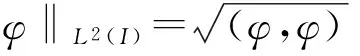
则L2(I)可看成L2(Ω)的子空间。设M1>0,M2>0,记人口系统的控制集为

c(r)≤M1,0≤b(r)≤M2,a.er∈I}。

对于L2(I)×L2(I)中元素,定义范数：

‖(c,b)‖=‖c‖L2(I)+‖b‖L2(I)。

对U中元素取L2(I)×L2(I)范数,则不难看出U为L2(I)×L2(I)的闭凸子集。定义:

H1,2(Ω)中范数定义为

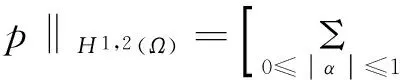
由Soblev嵌入定理,得到嵌入

H1,2(Ω)→L2(Ω)。

H1,2(Ω)可看成L2(Ω)中的完备子空间。任取(c(r),b(r))∈U代入问题(3)得到系统方程(1)存在唯一解p(r,t)。设p*(r,t)为人们追求的理想状态,定义指标泛函J为

J(p)=J(c,b)=‖p(r,t;b,c)-p*(r,t)‖L2(Ω)。

当控制变量(c(r),b(r))取遍整个U,对于确定的p(t)可表示集合W为

存在(c(r),b(r))∈U,使得方程(1)对应解为p(r,t;b,c),且

以下为表述方便,记

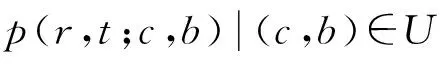
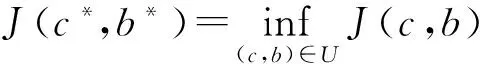
2　主要结果

定理1W是L2(Ω)中的有界闭凸集。

证明W的有界性直接由式(3)估计即得。

(1)闭性。

当n→∞时有p(r,0)=p0(r),r∈[0,rm),故p满足初始条件。

对边界条件:由于{βn}有界,所以有弱收敛子列:

结合在L2(Ω)中pn→p,可得i→∞时,在L2[0,T]中

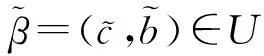
(2)凸性

设β1=(c1(r),b1(r))∈U,β2=(c2(r),b2(r))∈U,对应的p1=p1(r,t),p2=p2(r,t)∈W,λ1,λ2≥0,λ1+λ2=1,p=λ1p1+λ2p2,代入式(1)中,则p满足以下问题:

由U的凸性知:(λ1c1+λ2c2,λ1b1+λ2b2)∈U；

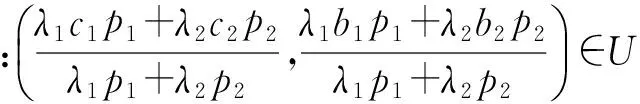
定理2人口系统问题(1)在U中存在唯一的双最优控制元(c*(r),b*(r))。

证明设J(p)=J(c,b)=‖p(r,t;b,c)-p*(r,t)‖L2(Ω),由解(3)对参数函数(c(r),b(r))的连续依赖性,当(c(r),b(r))在有界集U中取值时,W亦为有界集。又设pn∈p(U)是极小化序列,相对应U中的双控制元为(cn(r),bn(r)),

由于{pn}在L2(Ω)中有界,由定理1知W为L2(Ω)中的有界凸集,故能自{pn}中选子列(不妨设其自身),使得

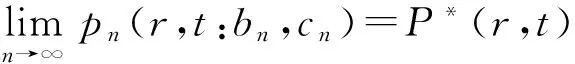
由Mazur定理,存在{pn}的凸组合序列

使得

(5)

强收敛。

这里，U中与Sm相应的双控制元为(cm(r),bm(r)),由定理1中闭性可得(cm(r),bm(r))强收敛于(c*(r),b*(r)),从而(c*(r),b*(r))∈U,且p*(r,t)为系统(1)的与(c*(r),b*(r))相对应的解。由于J为空间L2(Ω)中的范数函数,故J为严格凸函数。注意到{pn}是极小化序列,有

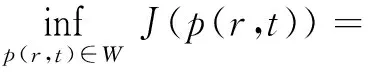
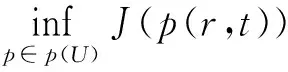
结合式(5)得

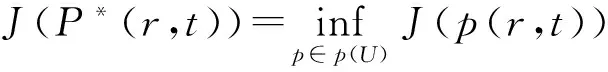
由上，(c*(r),b*(r))是U中人口系统(1)的双最优控制元。最后,由J的严格凸性知p*(r,t)是唯一的,从而得(c*(r),b*(r))亦是唯一的。

[1]宋健, 于景元. 人口控制理论[M]. 北京: 科学出版社, 1985.

[2]宋健, 于景元. 人口系统稳定性理论和临界妇女生育率[J]. 自动化学报, 1981, 17(01): 1-12.

[3]宋健, 于景元, 朱广田, 等.人口发展方程解及其渐进性质[J]. 科学通报, 1982, 27(22): 1356-1359.

[4]谷超豪, 李大潜, 沈玮熙. 应用偏微分方程[M]. 北京: 高等教育出版社, 1993.

[5]黄炯. Verhulst型偏微分方程人口模型整体解的存在唯一性研究(I)[J]. 云南师范大学学报： 自然科学版, 1999, 19(6)： 28-39.

[6]WANG HUI, HOU XUEZHANG. A control problem for nonstationary population systems[J]. Journal of Systems & Science Systems Engineering, 1994, 3(1): 66-73.

[7]蔡吉花, 王辉, 石端银. 时变人口发展系统非竞争人口生育率的最优控制[J]. 数学的实践与认识, 2006, 36(9): 265-270.

[8]蔡吉花. 时变人口发展系统竞争生育率的优化控制[J]. 黑龙江科技学院学报, 2007, 17(6): 483-485.

(编辑晁晓筠)

Two control elements problem of fertility rate for population developing system

CAIJihua,CONGLingbo

(College of Sciences, Heilongjiang Institute of Science & Technology, Harbin 150027, China)

This paper presents a study on the time-dependent population developing system and discusses the optimal control problem of the time-dependent population developing system by regarding the noncompetitive fertility rate and the competitive fertility rate as two control elements. The existence and uniqueness of the optimal control for the time-dependent population developing system are proved by the functional analysis methods.

population developing system; fertility rate; closed convex set; two control elements

1671-0118(2012)01-0089-04

2012-01-04

黑龙江省自然科学基金项目(A200915)；黑龙江省教育厅科学技术研究项目(10551285)

蔡吉花(1963-),女,黑龙江省尚志人，教授,硕士，研究方向：微分方程,E-mail:caijh2003@163.com。

O29； C923

A