低渗透气藏产能方程的改进

解庆阁 刘志斌 刘道杰 王天柱

（西南石油大学，成都610500）

低渗透气藏产能方程的改进

解庆阁 刘志斌 刘道杰 王天柱

（西南石油大学，成都610500）

低渗透气藏在成藏机理上与中高渗透气藏存在较大差别，若将中高渗透储层的开发理论和技术应用于低渗透储层必将产生较大误差。通过分析致密气藏成因、储层特征及渗流机理，考虑影响低渗透气藏渗透率的因素，将低渗透气藏低速渗流的指数式方程简化为达西渗流方程，建立改进的低渗透气藏产能方程，并给出该方程的求解方法。通过实例分析论证了此方法的可靠性和实用性。

低渗透气藏；渗流机理；产能方程；无阻流量

目前低渗透和特低渗透气藏的开发还存在一些技术上的难题。一般情况下，气藏中的流体在原始压力条件下处于单一的气态，在气藏的开发初期不会存在大的问题［1-4］。但是随着开发的进行，地下流体不断被采出，气藏压力就会不断下降，气相流体中的重烃组分就会发生相间传质和相态变化，在井底和近井地带出现凝析液，形成气液两相流，造成井底积液，导致井底的流体流动形态的复杂化，对气井产量的分析等产生不利的影响。同时，经室内实验证实：在一定条件下，气体的渗流存在“滑脱效应”和“启动压力梯度”，使得气体渗流偏离达西线性流［5-7］。

气井产能是指气井的生产能力［8-10］。气井产能的度量通常采用绝对无阻流量。对于低渗透气层，压力在很长时间内（数月或数年）都不会达到稳定。而且地层压力和井底流压也不可能变成常数。

1 致密气藏成因及特征

致密气藏的成因和其他高渗透气藏的成因不同。近物源沉积的颗粒混杂、分选差，远物源沉积的颗粒细、泥质含量高、矿物成熟度低；成岩压实作用强、伴有裂隙、出现双重孔隙带，空隙个体小、吼道细微孔喉多。一般而言，致密气藏的孔隙结构特征具有以下特征：随着渗透率的降低，排驱压力增加，驱动压力增加，孔隙的分选性变差，其退汞效率降低，岩石的比表面积增加，孔隙直径减少，喉道半径逐渐减小，最终驱油效率降低。

由于致密渗透气藏的形成原因比较特殊，尤其受黏土类型以及形成过程中的压实作用，其渗流机理与常规的气藏流体的渗流机理不同，主要表现为Klinkenberg曲线特征，毛管力与渗透率以及相渗曲线关系，致密气藏的孔隙结构特征。

根据Klinkenberg的理论（不含束缚水的多孔介质中气体单相渗流），岩心的气测渗透率与平均压力的关系为：

式中：Kg—气测渗透率，μm2；K—绝对渗透率，μm2；b—气体滑脱因子；Pm—平均压力，MPa。

Klinkenberg根据实验得出：启动压力梯度随着含水饱和度的增大而减小。

众多学者研究认为，低渗透储层中气、水流动需要通过的通道很窄，在细小的喉道处容易形成水化膜，底层中的气体从静止到流动必须突破水化膜的束缚，作用于水化膜两侧的压力差达到一定的大小是气体开始流动的必要条件，这种压力梯度就是气体渗流时的启动压力梯度，并且渗透率越小启动压力梯度越大。在试验中还发现，当流动压差减小到一定程度后，低渗岩心中见水后渗流就会停止，即气水两相要保持连续流动也必须要保证一个最低的压差，称其为临界压力梯度。

2 改进的二项式产能方程

假设均质致密气藏中心一口井定量生产，忽略重力和毛管力的影响，考虑井筒储集效应、表皮效应和气体的滑脱效应。那么考虑气体滑脱效应影响的致密气藏中定产量生产问题的试井分析数学模型可以写为：

式中：ψkD—无因次拟压力ψkwD—井底无因次拟压力；ψk—拟压力，f(p)d p；tD—无因次时间，；rD—无因次距离，rD=r/rw；CD—无因次井筒储存常数，CD=；S—表皮系数。

利用Laplace变换可以求解上述方程，其模型在Laplace空间上的解为：

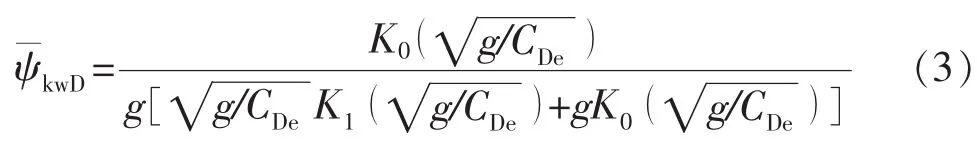
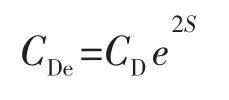
考虑启动压力梯度，根据拟压力的定义，定义拟启动压力梯度λψB：

因此有无因次拟启动压力λψBD：

由叠加原理可以得到任意产量下的压降通式，即：

式（7）即为改进的二项式产能方程。

根据上面的二项式产能方程，求出不同产量下的ψ′wfn以及相应的产量，根据每一产量下的qwfn和 ψ′wfn作。根据数据做直线进行回归，由直线的斜率和截距即可求出实际无阻流量：

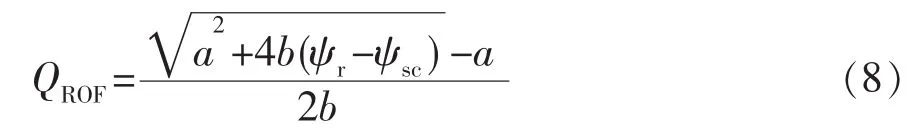
3 方程求解

假设实测的地层静压Pe′和真正的地层静压Pe存在误差δ1，实测的井底流压P′wf和稳定的井底流压Pwf存在误差δ2，则有：

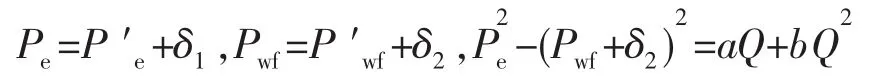
代入上面的二项式方程则可以得到一个关于a，b，δ2线性方程组。

根据叠加原理以及上面的公式推导，就能得到n-1个关于a，b，δ2的线性方程，求解线性方程并根据测试数据点则可以再得到一个线性方程组：

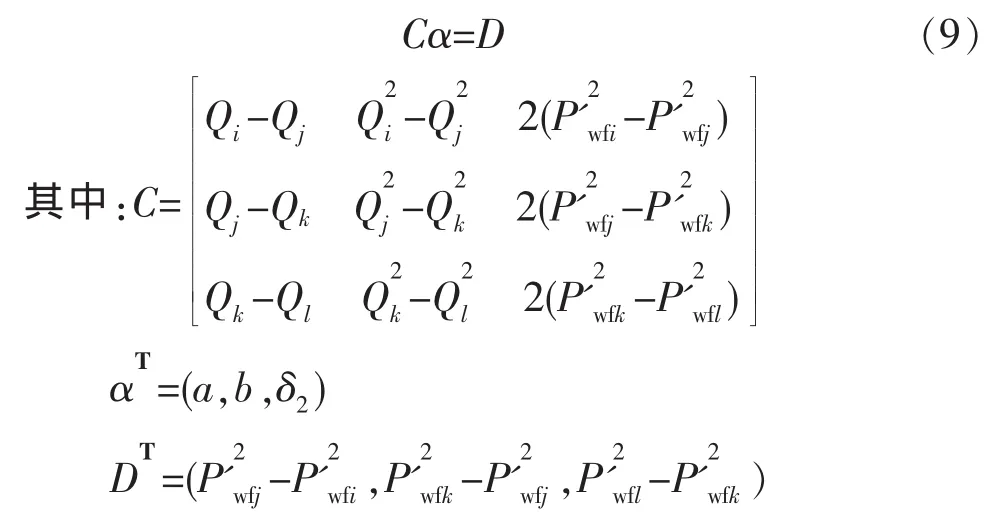
求解线性方程组（9）就得到一系列的a，b，δ2的值，继而可求得a，b，δ2的平均值。

4 实例分析

某油田区块中一口井X，原始地层压力40.2MPa，压力恢复解释原始地层压力32.45 MPa，储层温度326K，储层有效厚度8.0m，储层孔隙度20%，储层含水饱和度50%，井底半径0.078m，天然气相对密度0.61，天然气黏度0.03mPa·s，储层总的压缩系数0.018 3MPa-1。

平均地层压力采用产能方程计算获得，根据最优化分析计算的结果确定的产能方程的数据见表1。

表1 确定产能方程的数据表

图1 改进的产能方程拟合曲线

将表1中的数据绘制在直角坐标系内（图1），回归出一条直线方程：

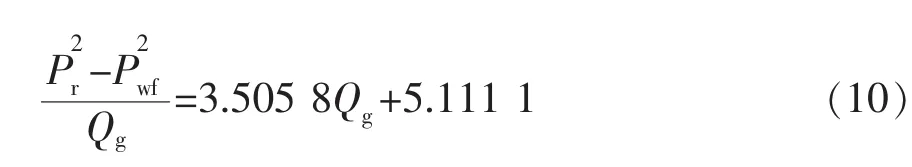
由式（10）整理得到产能方程：

由式（8）得到实际无阻流量：

5 结论

运用改进的等时试井分析对数据进行处理的结果显示，拟合曲线的斜率为负值，采用常规气藏不稳定产能分析方法分析数据时，公式中的地层压力使用原始地层压力，经过计算，生产井的实际无阻流量无解，即二项式产能方程无解；地层压力采用压力恢复的解释结果，二项式产能方程亦无解，因此本文提出的改进的二项式产能方程具有广泛的实用性，且准确性较高。

[1]戴强,段永刚,陈伟,等.低渗透气藏渗流研究现状[J].特种油气藏，2007，14(1):10-14.

[2]李松泉,程林松,李秀生,等.特低渗透油藏非线性渗流模型[J].石油勘探与开发，2008，35(5):606-612.

[3]时宇,杨正明,黄延章.低渗透储层非线性渗流模型研究[J].石油学报，2009，30(5):731-734.

[4]薛国庆,李闽,罗碧华,等.低渗透气藏低速非线性渗流数值模拟研究[J].西南石油大学学报：自然科学版，2009，31(2): 163-166.

[5]张俊,郭平.低渗透致密气藏的滑脱效应研究[J].断块油气田，2006，13(3):54-56.

[6]吴家文,贺凤云,李树良,等.考虑压敏和滑脱效应的低渗透气藏渗流规律研究[J].钻采工艺，2007，30(6):49-51.

[7]李冬瑶,程时清,郑春峰.考虑滑脱效应的低渗透气藏压裂井产能分析[J].特种油气藏，2009，16(2):59-61.

[8]李源源,王怒涛,黄炳光,等.低渗透气藏不稳定产能分析方法[J].断块油气田,2008,14(5):73-75.

[9]李冬瑶,程时清,郑春峰.考虑滑脱效应的低渗透气藏产能公式分析[J].石油天然气学报：江汉石油学院学报，2009，31(2):138-141.

[10]李乐忠,李相方,何东博.考虑变启动压降的低渗透气藏产能方程的建立[J].石油钻探技术，2010,38(1):89-92.

M odified Deliverability Equation of Low Percolation Gas Reservoir

XIE Qingge LIU Zhibin LIU Daojie WANG Tianzhu
(SouthwestPetroleum University,Chengdu 610500）

Using the theory and the technology which are fit for the high percolation gas reservoirs in the low ones w illmakemistakes.Because the low reservoirs are different from the high ones in mechanisms when they are formed.Analyzing the causes of formation,charaters of reservoir,influent mechanism,and other factors influencing the permeability of low percolation gas reservoir,this article takes exponential equation of low percolation reservoir simply as Darcys flow equation and provides a solution to the equation,but including the influence of critical flow velosity and pressure gradient.The case shows that the new method is reliable and practical.

low percolation gas reservoirs；influentmechanism；deliverability equation；open flow potential

TE155

A

1673-1980（2012）03-0068-03

2012-02-27

国家自然科学基金项目（50874094）；高等学校博士学科点专项科研基金项目

解庆阁（1981-），男，西南石油大学在读硕士研究生，研究方向为低渗透气藏渗流机理。