深基坑施工变形预测VAR建模与应用分析

代春泉，王 磊

（1.山东科技大学 土木建筑学院, 山东 青岛 266590；2.山东科技大学 山东省土木工程防灾减灾重点实验室，山东 青岛 266590）

1 引 言

随着经济社会的发展，城市人口的增加，城市规模在横向延伸的同时也在向纵向拓展，体现为城市建筑高度的增加和密度的增大，深基坑施工问题越来越突出，尤其在大中城市中深基坑施工面临问题更多，呈现出深大、近紧的特点[1－3]。施工过程中的各个环节都有可能引发恶性的工程事故，严重影响周边居民生活与社会生产，不仅带来巨大的经济损失，还严重影响正常的社会文化生活。基坑施工稳定性控制问题一直是国内外专家研究的热点，历经几十年的研究与发展，取得了大量的、有价值的研究成果。

在基坑施工变形力学分析方面，Thomas[4]通过对大量实测数据和模型试验结果的比较，得出墙体位移与地表沉降的变化规律；OU Changyu等[5]研究了挡墙最大位移位置、大小，挡墙最大水平位移与最大地表沉降的关系，最大地表沉降的位置，并给出了开挖显著影响区范围。Attwell[6]探讨了地下工程或基坑开挖引起的地面沉降，以及对地面建（构）筑物和地下管线的影响。Nakai[7]采用MITE3模型模拟分析了Boston深基坑开挖变形分布，以及对周边建筑物的影响，通过对基坑开挖侧向变形的数值模拟分析总结，认为最大侧向变形是开挖深度和支撑间距的函数。侯学渊等[8]根据墙体水平位移和地表沉陷相关原理，并借用三角形沉降公式采用有限元方法，分析了地面沉降和墙体水平位移的分布规律。刘国彬等[9]结合上海轨道交通地铁深基坑变形监测，对不同坑底暴露时间所对应的支护墙体变形分布进行了综合分析。龚晓南等[10]采用三维有限元理论，分析了深基坑施工过程支护结构的内力分布规律，以及土层应力分布的空间规律和变形特 征，并对基坑开挖力学问题的尺寸效应进行了探讨性研究。

上述专家从不同角度采用不同方法研究了基坑施工变形力学问题，这些成果对揭示基坑施工变形力学机理，定性分析基坑施工变形分布规律方面具有重要意义。但是，随着基坑施工规模增大，深度增加，传统力学问题并不能定量解决深基坑变形分析与稳定性控制难题，于是一部分专家寻求新的途径——变形预测分析基坑施工变形问题。

所谓变形预测是采用数理统计方法，如灰色理论、神经网络方法、随机理论等建立预测模型，以基坑施工前期部分监测数据为样本预测其后一定时间内的变形发展。这一方面的主要研究成果有，缪新颖等[11]对传统的 BP神经网络变形预测进行改进，提出了具有较快收敛速度和较强泛化能力的LM-BP变形预测模型。廖展宇等[12]采用非等间距时序灰色预测模型分析了基坑施工变形的时间变化特征，经过工程实例分析，该模型精度高，满足中期预测分析要求。贾备等[13]则将灰色系统理论与BP神经网络模型进行有机联合，建立了灰色BP神经网络组合模型的预测方法。李水兵等[14]采用双曲正切函数作为输入输出的传递函数，建立了深基坑变形预测的BP神经网络预测模型，并采用附加动量法对模型进行自适应修正。刘开云等[15]根据现场监测分析了边坡位移序列的非线性特点，采用模糊神经推理系统和遗传算法，建立边坡变形预测的进化-自适应神经网络模糊推理模型，并进行了实例验证分析，分析结果表明该模型比传统的GA-SVR模型、GA-BP模型精度高。沙成满等[16]针对现场监测数据与实际变形值的偏差，以小波去噪理论，建立改进的灰色自适应变形预测模型进行深基坑施工变形预测分析，并进行了初值修正和残差分析，经过工程实例验证，该模型具有较高的精度。

从上述研究成果来看，变形预测已成为基坑施工既有支护效果评价，施工安全预警的重要方法。但是根据实际应用情况，基坑施工变形预测还存在精度低，预测时效性差的问题。

向量自回归模型（VAR）及其衍生模型因其应用方便、预测精度高等优点在金融分析、经济预测等领域得到广泛应用，本文尝试采用 VAR模型预测深基坑施工变形。

2 深基坑变形预测与VAR模型

2.1 变形预测基本原理

目前我国深基坑施工设计还是以经验设计为主，施工过程中以监测信息反馈为指导修正既有支护方案，并分析施工安全性。传统方法认为，监测值趋于稳定变意味着支护结构的安全性[17]。这种模式监测信息反馈具有滞后性，不能及时调整支护参数，支护调整越滞后，支护成本越高，而且容易引起变形失控，引发工程事故。因此根据既有的监测数据建立数学预测模型及时调整支护参数，对优化施工方案、调整支护参数、保障施工安全具有重要意义。变形预测以既有支护条件下变形监测数据为小样本，通过一定的数学模型进行预测分析，检查模型精度并调整进而服务于基坑施工，具体流程如图1所示。

图1 基坑施工变形预测流程Fig.1 Prediction flow of construction deformation of foundation pit

2.2 基坑变形实测分析

向量自回归模型VAR于20世纪90年代在经济、金融等领域得到广泛应用[18－19]，到本世纪初开始在工程领域应用，如风速预测、浪高预测、水流预测、降水预测等[20－21]。

基坑施工变形监测数据一般以天(d)为单位绘制变形曲线，如图2所示。

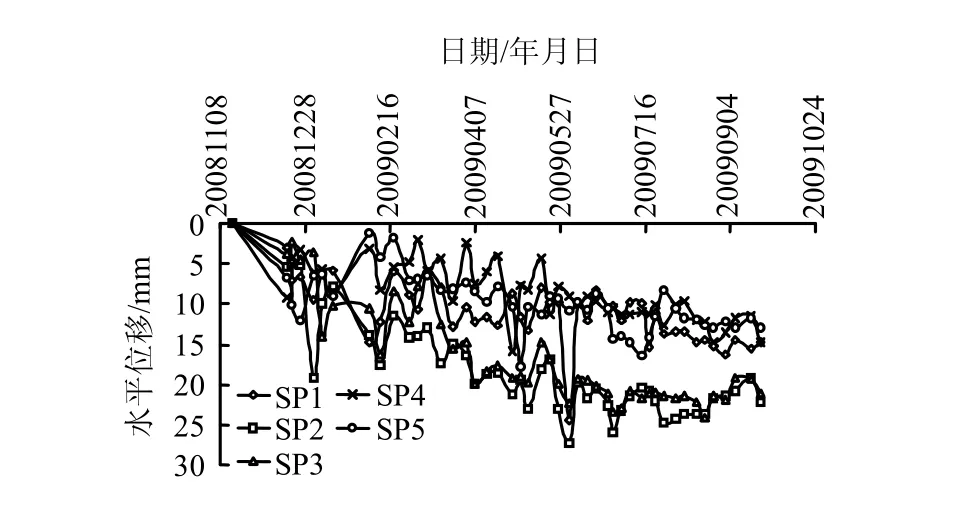
图2 基坑施工变形实测曲线Fig.2 Measured curve of construction deformation of foundation pit

从图2的基坑施工变形实测曲线来看，变形呈现波动规律，但从长期变形发展来看又有一定的规律可循，而这种短期非平稳、长期有规律的变形特点适合采用VAR模型进行建模预测分析。

2.3 基坑变形预测VAR模型

将基坑变形监测数据以时间序列记为U(t)，t =1, 2, …, n的单位时间间隔，根据不同分析的需要可取△t为1、2、10、30 d等。同一天内不同监测时间的变形-时间序列写为向量的形式，即

式中：下标d表示测试日期天数；下标k为向量维数，表示每天监测的次数。

对于式（1）中向量变形-时间序列Ud，可以建立n阶的VAR模型：

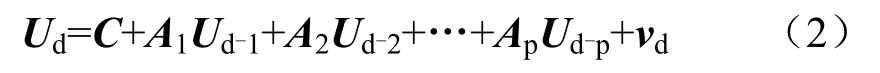
式中：Ai为模型参数矩阵，可根据已监测数据求得；vn是均值为0的分布相同的噪声向量；C为常数向量。

对式（2）作均值处理，可得

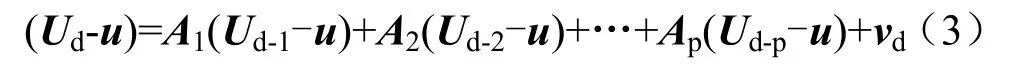
式中：u为建模样本数据均值。

为简化分析，定义以下向量和矩阵：

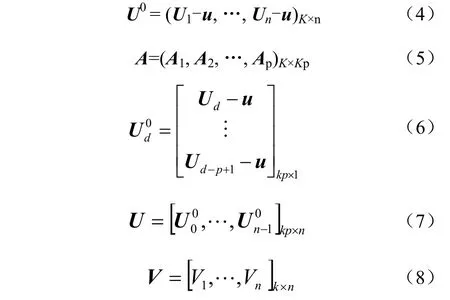
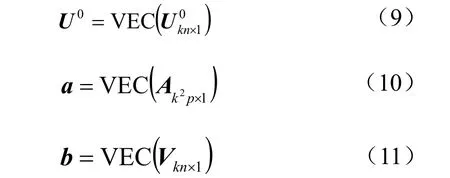
因此可将式（3）改写为

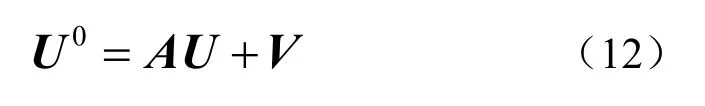
进一步可将式（12）写为

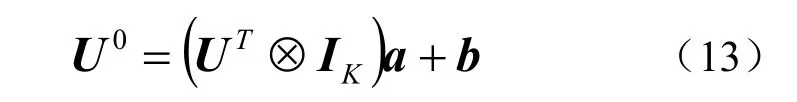
式中：IK为K阶单位矩阵。

取对数似然函数：

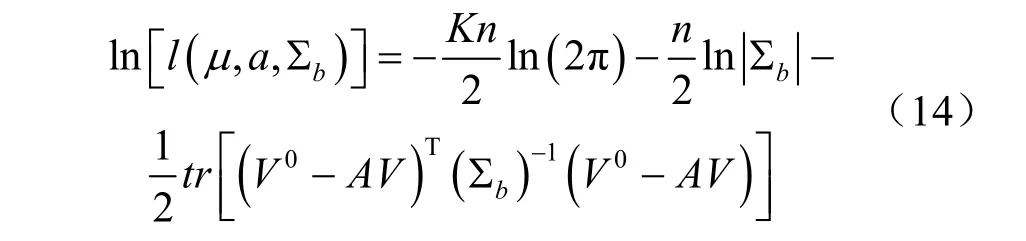
式中：∑b为V的协方差矩阵。

分别对式(14)似然函数求偏导数，便可得到参数矩阵a、b。

而对于模型阶数的确定，可采用似然比统计量法或AIC法(赤木信息判据)，这里采用AIC法，即

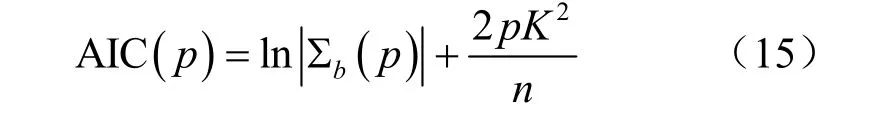
式中：∑b（p）为协方差矩阵∑b极大似然估计。

AIC法计算的具体步骤为：对p=0, 1, 2, …, n，分别计算模型参数，并计算AIC(p)，其最小值对应的p值就是VAR模型所需要的阶。

2.4 VAR模型应用说明

从上述建模过程来看，计算比较复杂，实际应用过程中，由于一般监测为1 d1～2次，维数降为一维或二维，使得求解过程更加简单。分析过程中可借助excel或matlab编程计算。

3 深基坑施工变形预测应用分析

3.1 工程概况与施工监测

济南市省会文化艺术中心深基坑工程最大开挖深度为21.2 m，开挖深度范围内有流砂层，且濒临黄河，地下水丰富。基坑施工难度大，而且工程规模大，基坑施工将跨越夏季多雨季节，对基坑安全不利。在施工过程中通过设计了合理的监测方案，密切关注施工过程中各监控值的变化，并建立预测模型预测变形发展趋势，及时优化施工方案，保证施工安全。

3.2 预测应用分析

为检验文中给出的 VAR模型在深基坑施工变形预测中的应用效果，以坡顶竖向位移典型数据为样本建立模型，进行变形预测。取图2中典型测点SP2前期监测数据，如图3所示。

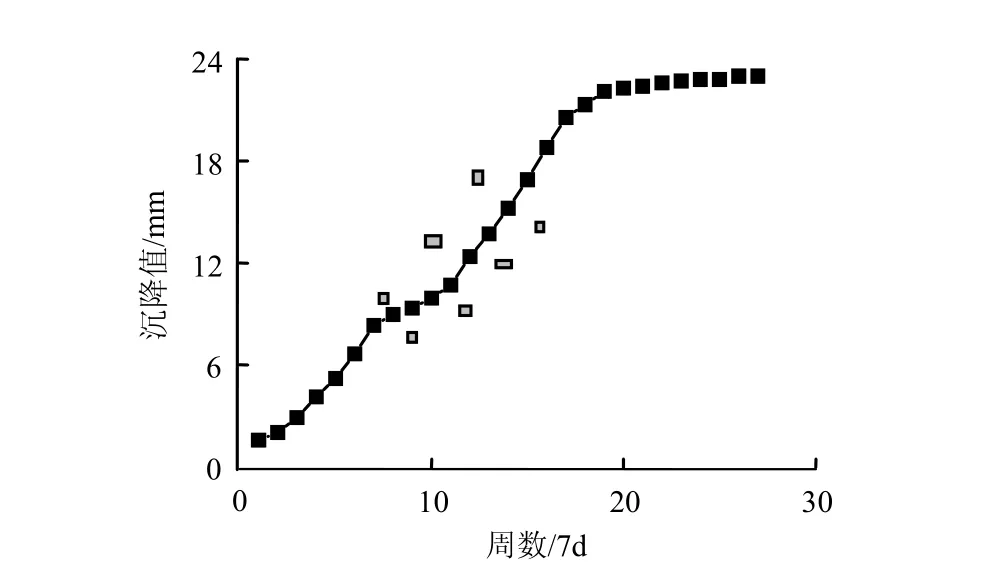
图3 SP2监测曲线Fig.3 Measured curve of point SP2

以前35 d数据为样本建立模型，根据AIC比较，取p=2，经过计算，预测值误差分析见表1。

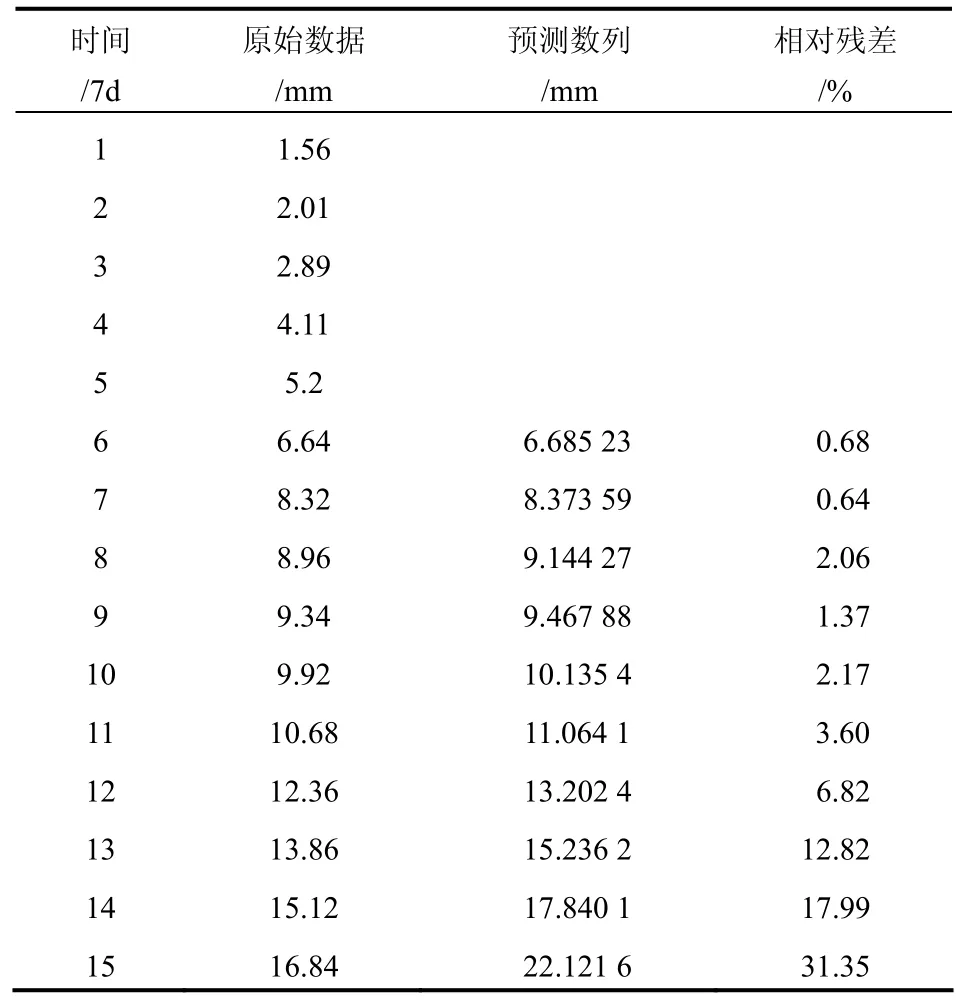
表1 VAR模型预测分析Table 1 Analysis of VAR model

根据表1中分析数据，VAR模型以前期监测数据为样本建立模型，并且及时补充新数据，预测后期变形发展，在77 d之前误差较小，77 d之后误差明显增大，98 d之后已经不可接受。

通过误差分析，该模型进行深基坑施工变形短期预测误差可以接受，模型精度可以满足现场应用要求。

3.3 对比分析

为进一步分析 VAR模型的预测应用效果，选取目前常用预测模型：灰色预测模型 GM(1,1)、新陈代谢模型和神经网络预测模型进行建模对比分析。GM(1, 1)模型是以小样本建立白化响应式，进而求解白化微分方程，建立变形预测数列。而新陈代谢模型则是在 GM(1,1)模型的基础上及时去掉旧信息，输入新信息，模型精度要比 GM(1,1)高；神经网络预测通过建立模型进行训练获得预测值，需要的信息量较大。以图3中数据进行建模预测分析，并计算相应的误差，计算结果如表2所列。

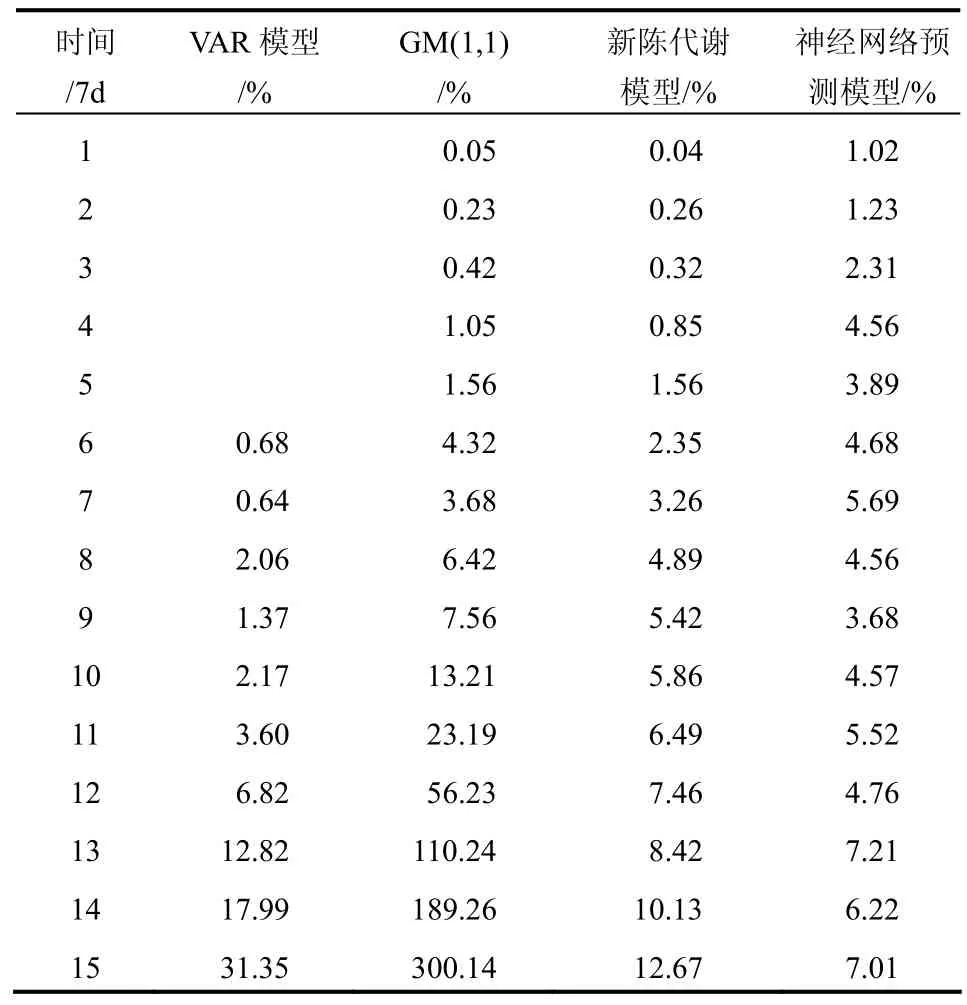
表2 4类预测模型预测精度分析Table 2 Analysis of 4 prediction models

由表2的预测结果可以看出，（1）VAR模型的预测精度要比GM(1, 1)模型、新陈代谢模型、神经网络预测模型精度高；（2）VAR模型、GM(1, 1)模型、新陈代谢模型都出现误差积累，后期预测精度低，只适合于短期预测，而神经网络模型在实际应用中需要的数据样本较多，其预测误差相对稳定，误差的大小与传递函数有关。

为分析4类预测模型的可预测时间段长与建模段长的关系，定义预测比，即

式中：ty为可接受的预测时段长；tj为建模时段长。

以相对误差5%为标准进行分析，可得VAR模型的预测比κ为 1.0，GM(1, 1)模型的预测比κ为0.4，新陈代谢模型的预测比κ为 0.6，神经网络预测模型由于其建模需要样本数据多，预测比为0.56。

4 结 论

（1）深基坑施工过程中受多种因素影响，根据实际基坑施工变形监测数据，从短期分析来看，数据具有非稳定性，但从长期分析又有一定的规律，可以用向量自回归模型进行建模分析。

（2）VAR模型在实际应用过程中，因一般监测频率为 1次/天或 2次/天，在分析过程中使得模型降为一维或二维，计算过程简化，而VAR模型的阶一般为2或3，极少超过5。

（3）4类预测模型从预测精度上比较，依次是：VAR模型＞新陈代谢模型＞神经网络模型＞GM(1,1)模型；而建模所需要的样本量排序为：神经网络预测模型＞新陈代谢模型＞VAR模型＞GM(1, 1)模型。

（4）VAR模型不适合长期变形预测，适合于短期变形发展分析，4类模型的预测比排序为：VAR模型＞新陈代谢模型＞神经网络模型＞GM(1, 1)模型。

[1] 徐中华，王建华，王卫东.上海地区深基坑工程中地下连续墙的变形性状[J].土木工程学报, 2008, 41(8): 81－86.XU Zhong-hua, WANG Jian-hua, WANG Wei-dong.Deformation behavior of diaphragm walls in deep excavations in Shanghai[J].China Civil Engineering Journal, 2008, 41(8): 81－86.

[2] OSMAN A S，BOLTON M D.Ground movement predictions for braced excavations in undrained clay[J].Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 2006, 132(4): 465－477.

[3] 黄茂松, 宋晓宇, 秦会来.K0固结黏土基坑抗隆起稳定性上限分析[J].岩土工程学报, 2008, 30(2): 250－255.HUANG Mao-song, SONG Xiao-yu, QIN Hui-lai.Basal stability of braced excavations in K0-consolidated soft clay by upper bound method[J].Chinese Journal of Geotechnical Engineering, 2008, 30(2): 250－255.

[4] THOMAS D, ROURKE O.Ground movement caused by braced excavation[J].School of Civ.and Environmental Engrg., 1981, 107(9): 1159－1178.

[5] HSIEH P G, OU Chang-yu, HSIEH.Shape of ground surface settlement profiles caused by excavation[J].Canadian Geotechnical Journal, 1998, 35(6): 1004－1017.

[6] ATTWELL P B.Soil movement induced by tunneling and their effects or pipelines and structures[M].New York:Soil Blackie Chapman and Hall, 1986: 2046－2046.

[7] NAKAI T.Analysis of earth pressure problems considering the influence of wall friction and the wall deflection[C]//Proc., the 5th Int.Conf.on Numer.Methods in Gechanics.Japan: [s.n.]: 765－772.

[8] 侯学渊，刘国彬，黄院雄.城市基坑工程发展的几点看法[J].施工技术，2000, 29(1): 256－261.HOU Xue-yuan, LIU Guo-bin, HUANG Yuan-xiong.Several views on the development of urban foundation work[J].Construction Technology, 2000, 29(1): 256－261.

[9] 刘国彬, 刘登攀, 刘丽雯, 等.基坑坑底施工阶段围护墙变形监测分析[J].岩石力学与工程学报, 2007, 26(增刊2): 4386－4394.LIU Guo-bin, LIU Deng-pan, LIU Li-wen, et al.Monitoring and analysis of lateral deformation of retaining wall during bottom excavation in deep pit[J].Chinese Journal of Rock Mechanics and Engineering,2007, 26(Supp.2): 4386－4394.

[10] 龚晓南.基坑工程发展中应重视的几个问题[J].岩土工程学报, 2006, 28(增刊): 1321－1324.GONG Xiao-nan.Some major problems in the development of foundation pit engineering[J].Chinese Journal of Geotechnical Engineering, 2006, 28(Supp.):1321－1324.

[11] 缪新颖, 褚金奎, 杜小文.LM-BP神经网络在大坝变形顶测中的应用[J].计算机工程与应用, 2011, 47(1): 220－222.MIAO Xin-ying, CHU Jin-kui, DU Xiao-wen.Application of LM-BP neural network in predicting dam deformation[J].Computer Engineering and Applications, 2011, 47(1): 220－222.

[12] 廖展宇, 李英, 晏鄂川, 等.非等间隔时序灰色模型的深基坑变形预测研究[J].合肥工业大学学报, 2009,32(10): 1522－1525.LIAO Zhan-yu, LI Ying, YAN E-chuan, et al.Study on deformation prediction of a deep foundation pit based on the unequal interval grey model[J].Journal of Hefei University of Technology, 2009, 32(10): 1522－1525.

[13] 贾备, 邬亮.基于灰色BP神经网络组合模型的基坑变形预测研究[J].隧道建设, 2009, 29(3): 280－284.JIA Bei, WU Liang.Research of the Prediction of foundation deformation based on gray BP neural network combined model[J].Tunnel Construction, 2009, 29(3):280－284.

[14] 李水兵, 李培现.基于 BP神经网络的深基坑变形预测[J].测绘信息与工程, 2011, 36(5): 41－43.LI Shui-bing, LI Pei-xian.Deep Foundation pit considering excavation effect based on BP neural network model[J].Journal of Geomatics, 2011, 36(5): 41－43.

[15] 刘开云, 魏博, 刘保国.边坡变形时序分析的进化自适应神经模糊推理模型[J].北京交通大学学报, 2012,36(1): 56－62.LIU Kai-yun, WEI Bo, LIU Bao-guo.Analysis model of slope deformation time series based on the genetic-adaptive neuron-fuzzy inference system[J].Journal of Beijing Jiaotong University, 2012, 36(1): 56－62.

[16] 沙成满, 韩合新, 杨冬梅.基于小波去噪的改进灰色自适应变形预测[J].东北大学学报, 2011, 31(8): 1195－1197.SHA Cheng-man, HAN He-xin, YANG Dong-mei.Deformation forecast using improved self-adaptive grey model based on wavelet denoising[J].Journal of Northeastern University (Natural Science), 2011, 31(8):1195－1197.

[17] 龚晓南.土钉和复合土钉支护若干问题[J].土木工程学报, 2003, 36(10): 80－83.GONG Xiao-nan.On soil nailing and composite soil nailing[J].China Civil Engineering Journal, 2003,36(10): 80－83.

[18] 吴振信, 薛冰, 王书平.基于 VAR模型的油价波动对我国经济影响分析[J].中国管理科学, 2011, 19(1): 21－28.WU Zhen-xin, XUE Bing, WANG Shu-ping.The impact of oil price volatility on China’s economy based on VAR model[J].Chinese Journal of Management Science,2011, 19(1): 21－28.

[19] HERRERA A M, PESAVENTO E.Oil price shocks,systematic monetary policy, and the great moderation[J].Macroeconomic Dynamics, 2009, 13: 107－137.

[20] 孙春顺，王耀南，李欣然.小时风速的向量自回归模型及应用[J].中国电机工程学报，2008, 28(14): 112－117.SUN Chun-shun, WANG Yao-nan, LI Xin-ran.A vector autoregression model of hourly wind speed and its applications in hourly wind speed forecasting[J].Proceedings of the CSEE, 2008, 28(14): 112－117.

[21] EWING B T, KRUSE J B，SCHROEDER J L, et al.Time series analysis of wind speed using VAR and the generalized impulse response technique[J].Journal of Wind Engineering and Industrial Aerodynamics, 2007,95(19): 209－219.