埋地管道弯管应力数值计算

吴玉国，周立峰，朱佳琦，李小玲

（1. 辽宁石油化工大学 石油天然气工程学院， 辽宁 抚顺 113001； 2. 中国石油辽河工程有限公司， 辽宁 盘锦 124010）

弯管广泛应用于管道系统当中，由于其形状和结构形式的复杂性导致其受力情况也比较复杂，而采用有限元分析方法，能够得到得到满足工程精度要求的应力解，为进行弯管结构可靠性分析和寿命分析提供依据［1］。

1 ANSYS12.0及有限元分析

ANSYS软件作为ANSYS公司开发的有限元计算分析程序，具有强大的、广泛的分析功能[2,3]。该软件采用了有限元分析法，有限元方法中一个物体或系统被分解为由多个相互联结的、简单的、独立的点组成的几何模型。将根据实际的物理模型推导出的平衡方程式使用于每个点上，便产生一个可以用线性代数的方法求解的方程组。

经过离散化处理的的有限元计算模型可以归结成为如下一线性方程组[4]：

式中： {F} —所受到的外力向量；

［K］—整体刚度矩阵；

{D} —模型中各个节点的位移向量。

［K］由每个单元对应的刚度矩阵叠加得到：

式中：［E］e—单元刚度矩阵。

公式（1）中所受的外力向量的表达式如下：

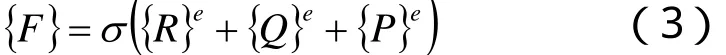
式中：{R}e—单元集中力；

{Q}e—单元表面力；

{P}e—单元体积力。

求出方程（1）中的各个系数并给定具体的边界条件，待求的有限元模型上各节点的位移{D}就可以被求出。先将单元上各节点的应变{E}求出，{E}=［B］{D}e，其中的［B］代表单元的几何矩阵，跟具体的单元类型有关系。然后依据弹性方程{R}=［D］{E}就能够将应力求出。

2 计算模型

一条φ720 mm×8 mm的埋地输油管线，其管道中心埋深处土壤自然温度为 15 ℃，内压为 4 MPa。所用管材的弹性模量为210 GPa，线膨胀系数为 12×10-61/℃[5]。

在建立管道模型时（本文以 90°弯头为例），管道截面应用plan42单元建立，之后进行相应的网格划分，在扫描线建立的基础上使用solid70热单元做三维单元扫掠，并将plan42单元删除。经过以上步骤最终得到如图1所示的模型及其网格。

3 结果分析

3.1 不同温度下的弯头应力

图 1 弯管模型及其网格划分Fig.1The bend pipe model and grid

输油温度为20 ℃和60 ℃时90°弯头所受到的应力情况如图2和图3所示。

图2 输油温度为20 ℃时弯头应力分布情况Fig.2 Stress distribution of the elbow when the transporting temperature is 20 ℃

从两图中显示出的弯头所受热应力的数值计算结果容易看出，弯头所受到热应力值随着输油温度的增加而增大，而且在不同输油温度下热应力具有相同的分布规律：应力主要集中于弯头的内半径附近的位置。

3.2 夹角、曲率半径对弯头应力的影响分析

弯头处所受应力还受到弯头夹角以及弯头曲率半径等的影响，为了探寻这些因素对于弯头所受应力的具体影响规律，非常有必要对不同夹角、曲率半径下的弯头所受应力进行计算与分析[5]。本文计算了 20°、60°和 90°的弯头在曲率半径R分别为D、2.5D 和 5D 情况下所受的应力。在计算过程中选择了4结点壳单元，并且沿着圆周方向每15°划分成1个单元，具体情况如图4所示。

图3 输油温度为60 ℃时弯头应力分布情况Fig.3 Stress distribution of the elbow when the transporting temperature is 60 ℃

图4 弯头横断面结点分布Fig.4 The node distribution at cross section of the elbow

所得的计算结果显示于图5至图12，每种计算条件下的计算结果图均包括两个，其中的左图是弯头所受应力分布云图，而右图是弯头的中间横截面内壁圆周各点处的应力值和应变值，右图中的蓝色曲线和红色曲线分别代表的是应力变化曲线和应变变化曲线，图中的横坐标代表的意义为沿着逆时针方向距圆周起点间的弧长。

图5 20°弯头曲率半径为D时的应力计算结果Fig.5 Stress of the 20°elbow with Dcurvature radius

图6 20°弯头曲率半径为2.5D时的应力计算结果Fig.6 Stress of the 20°elbow with 2.5Dcurvature radius

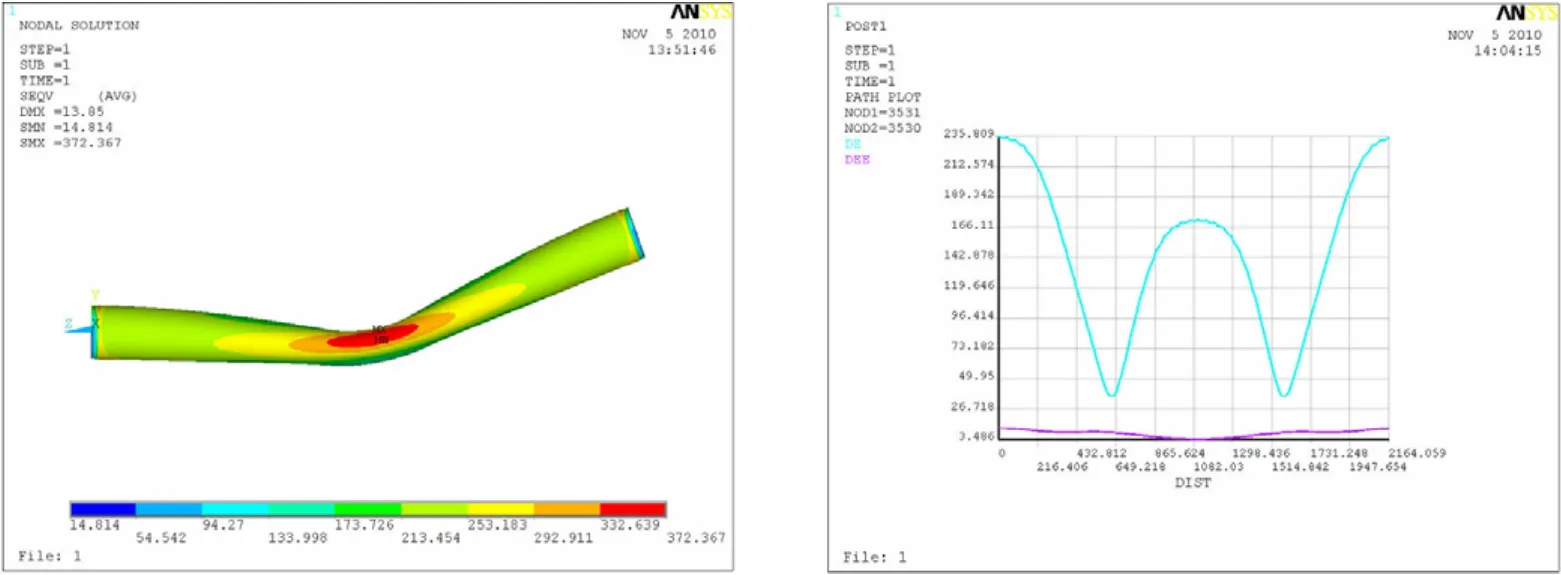
图7 20°弯头曲率半径为5D时的应力计算结果Fig.7 Stress of the 20°elbow with 5Dcurvature radius

图8 60°弯头曲率半径为D时的应力计算结果Fig.8 Stress of the 60°elbow with Dcurvature radius

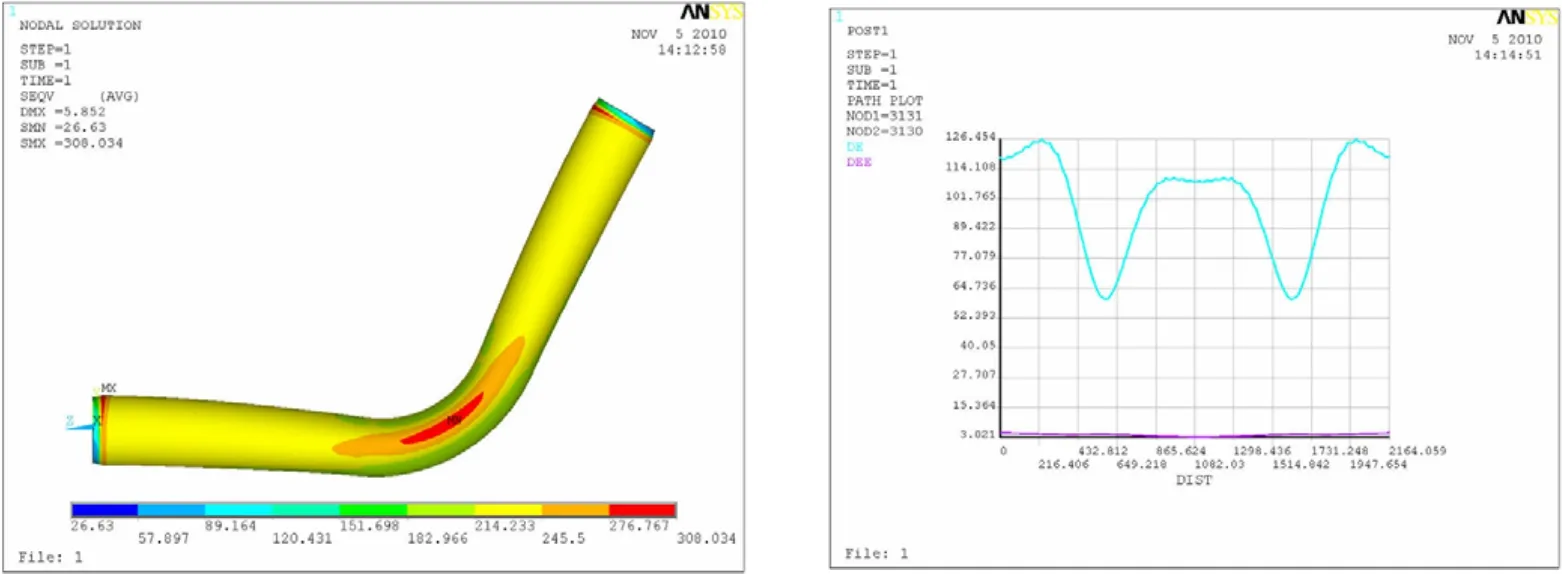
图9 60°弯头曲率半径为2.5D时的应力计算结果Fig.9 Stress of the 60°elbow with 2.5Dcurvature radius

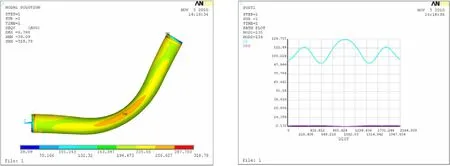
图10 60°弯头曲率半径为5D时的应力计算结果Fig.10 Stress of the 60°elbow with 5Dcurvature radius

图11 90°弯头曲率半径为D时的应力计算结果Fig.11 Stress of the 90°elbow withDcurvature radius

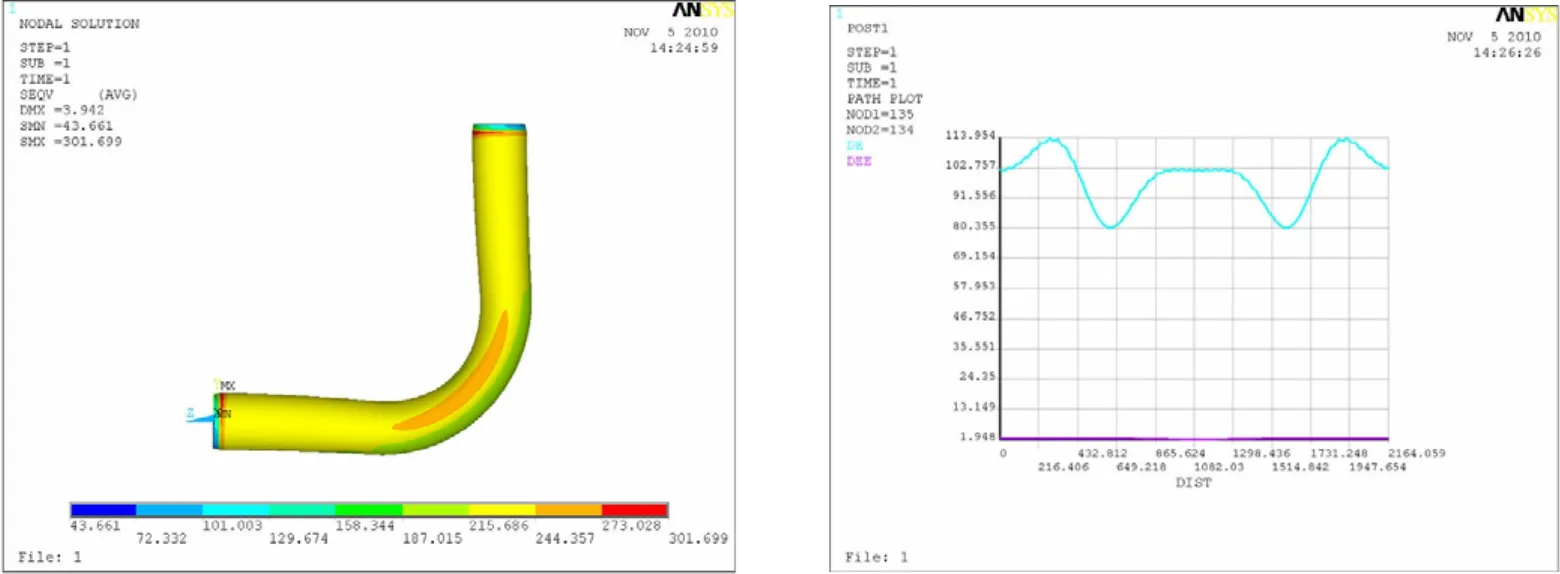
图12 90°弯头曲率半径为2.5D时的应力计算结果Fig.12 Stress of the 90°elbow with 2.5Dcurvature radius

将以上各个计算结果图进行对比、分析容易得出，在弯头夹角不变的情况下，弯头所受应力随着曲率半径的增加而减小。

正如图中所显示的，对于20°的弯头，曲率半径从D变化至5D，相对应的弯头所受最大的应力值从400 MPa左右降至330 MPa左右；对于60°的弯头，曲率半径从D变化至5D，相对应的弯头所受最大的应力值从 280 MPa左右降至250 MPa左右；对于90°的弯头，曲率半径从D 变化至2.5D时，相对应的弯头所受最大的应力从270 MPa左右降至240 MPa左右。

图13 不同角度弯头在不同曲率半径下的应力Fig.13 Stress of the elbows with diffrent angles and curvature radiuses

在弯头曲率半径保持不变的情况下，20°的弯头所受到的最大应力值最大，90°的弯头所受到的最大应力值则最小。具体数据以曲率半径均为D 的情况为例，20°的弯头所受到的最大应力值大约为400 MPa，而90°的弯头所受到的最大应力值大约为270 MPa。

以上的分析结论可以从图13中得到更好体现，图中反映出了不同角度（20°、60°）的弯头在不同曲率半径（D、2.5D、5D）条件下弯头所受最大应力的变化情况。

4 结 语

观察以上一系列的应力分布曲线图不难发现，在各种计算条件下的应力分布曲线形状大体上趋于一致，所以可按其中的一种情况来进行应力分布规律的说明，例如，60°的弯头在曲率半径为2.5D时，在圆周位置 30°～40°或 320°～330°位置附近的范围内呈现出较高的应力水平，在 90°～100°或 260°～270°位置附近的范围内呈现出较低的应力水平。

［1］ 马爱梅，鹿晓阳，孙胜.弯管应力分析及结构研究[J].机械设计与制造,2006, 44(3): 98-100．

［2］ 美国ANSYS公司.ANSYS基本过程手册[R].2002．

［3］ 美国ANSYS公司.ANSYS非线性分析指南[R].2002．

［4］ 刘士民.用ANSYS分析供热管道弯头热应力[J].盐城工学院学报(自然科学版),2006, 19(2): 26-30.

［5］ 吴玉国.冷热原油管道顺序输送技术研究[D].青岛:中国石油大学（华东）, 2010．