公交优先交叉口信号控制参数的多目标优化方法＊

李劲夫

(长沙理工大学交通运输工程学院，湖南长沙 410004)

公交优先交叉口信号控制参数的多目标优化方法＊

李劲夫

(长沙理工大学交通运输工程学院，湖南长沙 410004)

公交优先交叉口的信号控制方案应平衡车辆出行者时间效益、行人出行效率和环境效益，因此，需要基于多目标优化方法优化设计信号配时参数.首先，以车辆出行者人均延误、行人过街平均延误和停车率最小为目标构建信号周期多目标优化模型;然后，基于相位乘客流量比和相位饱和度优化设计绿信比;最后，构建了多目标优化模型的粒子群算法来寻找Pareto解.应用结果表明，相比常规方法，能根据决策者喜好选择Pareto解;可尽量降低车辆出行者的人均延误，在一定程度上体现了公交优先.

交通工程;信号配时;多目标优化;粒子群优化算法

周期时长和绿信比是信号控制配时的两个主要参数，传统的韦伯斯特法以车总延误最小为目标来确定周期时长和依据各个相位车流量比来分配绿灯时间.在各种交通方式混合通行的信号控制交叉口，为了提高乘客的平均出行效率，采用公交优先信号配时方法来优化周期和绿信比，是一种提高公交车优先通行的有效手段［1－7］.王正武等［1，2］设计了一种基于规则和基于优化的自适应公交优先控制方法.该方法基于规则选择优先车辆和优先策略，基于优化确定信号参数，并且降低了人均延误，体现了公交优先.张卫华等［3］、杨晓光等［4］提出以人均延误最小为目标来优化信号周期时长，以相位乘客流量比和相位饱和度确定绿信比，这种方法把公交车辆和社会车辆区分开来，减少了公交车通过交叉口的延误.马莹莹等［5］、钱小红等［6］、王秋平等［7］提出以机动车时间、行人时间及环境等综合效益指标构建多目标优化模型对信号参数进行优化，权衡了多个交通运行指标，考虑的是交通运行最优的综合效益.以乘客延误最小为目标的单目标优化方法，有可能对社会车辆造成一定的负面影响.考虑交通运行综合效益时，以机动车延误为目标，则不能体现公交优先的思想.本文针对公共汽车和慢行交通比例较大的信号交叉口，建立既体现交叉口公交车优先通行和快、慢交通协调运行，又不对社会车辆和环境有负面影响的信号参数多目标优化方法，并用粒子群多目标优化算法求解.

1 周期优化

1.1 优化目标

周期时长是交叉口信号配时的主要设计参数之一，传统Webster信号配时方法是以车总延误最小为目标来确定的.1997年，Jessica Anderson等人专门针对交通信号控制系统进行了系统研究，研究表明控制目标的选择应该多样化，且应随交通状态变化而对各目标的重要程度做相应的调整［8］.

混合交通通行下的交叉口考虑公交车优先通行，降低乘客平均出行时间，而且也考虑了对行人、非机动车交通的影响，信号交叉口周期时长与以下交通效益指标息息相关:人总延误、行人过街延误、车辆排队长度、交叉口通行能力、停车率、燃油消耗、废气污染、噪声污染等.以上指标可以归纳为三大类:车辆出行者时间效益、行人出行效率、环境效益.权衡三大指标效益，选取人均延误最小、行人过街延误最小、停车率最小作为周期时长的优化目标.

1.2 优化模型

从车辆出行者时间效益、行人出行效率、环境效益三方面出发，以人均延误最小、行人过街延误最小、停车率最小为目标.建立如下模型:

式中:f1(C)为人均信号控制延误;f2(C)为行人过街延误;f3(C)为机动车交叉口停车率;Cmin、Cmax分别为最小周期和最大周期;n为交叉口相位数;gk为相位k的绿灯时间;L为总损失时间;C为周期.

信号交叉口车辆延误的研究很多，其中美国《道路通行能力手册》中的延误模型研究成果较权威，本文采用HCM2000的交叉口车辆延误计算模型［9］，即

式中:dijk为相位k的i进口流向j出口方向对应的平均延误(s);xijk为相位k的i进口流向j出口方向的饱和流率;Cap为相位k的i进口车道通行能力(pcu/s);λk为相位k的绿信比;Pf、K、I为修正系数;T为分析期(h);d0为初始排队延误(s).

交叉口没有实施公交优先措施时，同一进口方向的社会车辆与公交车辆具有同样的延误.所以一个进口方向的人总延误应该等于该进口方向车均延误与车载乘客之积，交叉口人总延误等于各个进口方向人总延误之和.另外，本文考虑非机动车按机动车相位分流向通过交叉口，在交叉口设置非机动车待行空间，同时对右转机动车实行控制，避免在相位绿灯初期与非机动车冲突和干扰.因此，非机动车延误也可以以人总延误计入.即:

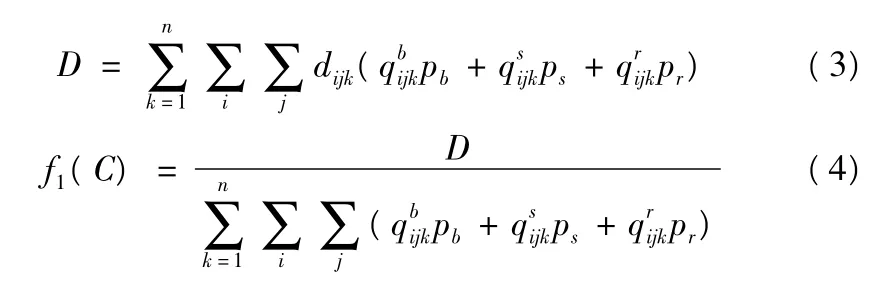
式中:D为一个周期交叉口人总延误;pb为公交车辆平均载客人数，ps为社会车辆平均载客人数，pr为非机动车平均载客人数，为相位k进口i到出口j方向公交车辆流到达率(pcu/s)，为相位k进口i到出口j方向社会车辆流到达率(pcu/s)，为相位k进口i到出口j方向非机动车辆流到达率(pcu/s).

信号控制交叉口行人过街平均延误［10］，主要是过街横道上行人过街在无干扰情况下，由控制信号产生的延误.

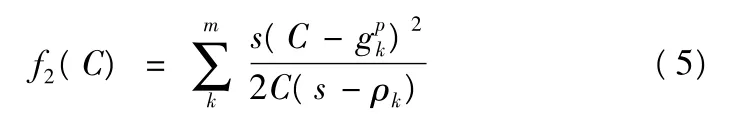
停车率模型按照Webster的计算方法建模［11］，即至少有一次停车(指完全停车)的车辆占通过交叉口车辆总数的比率，不考虑不完全停车的情况.停车率模型如下:

2 绿信比优化

一般交叉口信号配时方法中的相位绿信比是按车流量比来确定的，这种分配方法可以确保每个进口道方向具有相同的饱和度，但不利于公交车的通行.本文采用文献［3］的方法，减少交叉口的人均延误，绿信比由乘客流量比和机动车饱和度两个因素共同决定.

相位饱和度不大于某个给定值φ(建议取0.9)和相位绿灯时间不小于最小绿灯时间作为约束条件，来确定相位k的最小绿信比:

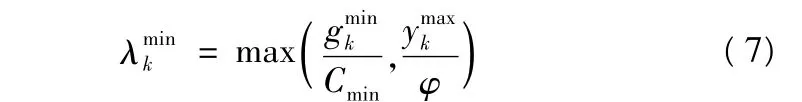
判断交叉口在满足各相位最小绿信比的前提下是否有过剩的绿灯时间:

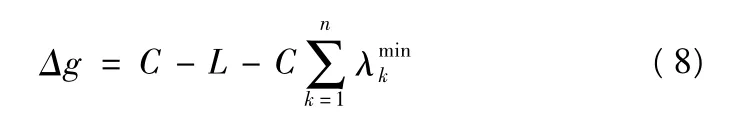
式中:Δg为交叉口总的过剩绿灯时间.

当Δg＜0时，表示交叉口通行能力不能满足现有交通需求，无过剩绿灯时间;当Δg=0时，能恰好满足现有需求，无过剩绿灯时间;当Δg＞0时，表示交叉口通行能力可以满足现有交通需求，并有过剩绿灯时间.当交叉口有过剩绿灯时间，需要将过剩的时间按照各相位客流量比来进行分配:

式中:Δgk为分配给相位k的过剩绿灯时间，pk为相位k客流量，pt为相位交叉口总客流量，则相位k的有效绿灯时间gk:

由上述(2)到(4)公式推导得出相位k绿信比λk为:

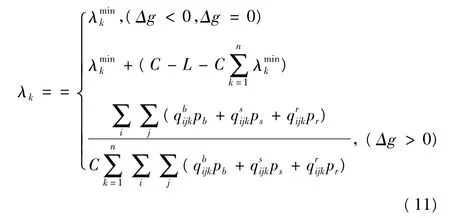
式中各符号意义同上.

3 模型求解

3.1 Pareto支配关系与最优解

为求解上述多目标优化模型，首先需要找出非劣解集和Pareto前沿，然后根据要求选取合理的解［12］.

b)设X∈Rn(可行解集合)，在Rn不存在比X更优的解X'，使得X'Pareto支配X，则称X为 Pareto支配的最优点.它们的集合称为最优解集，最优点所对应的目标值集合称为最优前沿.

3.2 粒子群多目标优化算法

多目标优化问题比单目标优化问题复杂得多，其Pareto最优解集也通常含有孤立最优点、凸的、非凸的、非均匀的区域，这些特点都会增加算法完成的难度.本文有三个目标函数，采用粒子群多目标优化算法求解.

粒子群优化算法首先初始化一群随机粒子，然后通过迭代找到最优解.在每一次迭代中，粒子通过跟踪两个“极值”来更新自己，同时也通过跟踪它们实现粒子间的信息交换.第一个就是粒子本身所找到的最优解，这个解叫做个体极值pBest.另一个极值是整个群体目前找到的最优解，这个极值是群体极值gBest.粒子在找到上述两个极值后，就根据下面的公式来更新自己的速度和位置［13］:

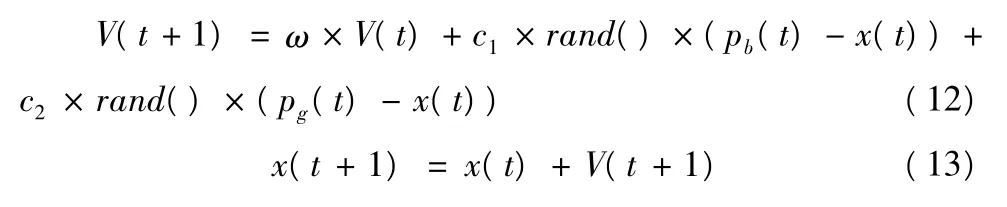
式中:c1、c2为正常数，称为加速因子;rand()为［0，1］之间的随机数;ω为惯性因子，V(t)、V(t+1)表示粒子的速度，x(t)、x(t+1)表示粒子的位置，pb(t)为个体最佳位置，pg(t)为群体最佳位置.

本文应用“精英集”来记录已找到的非劣解，并用这些非劣解来指导其它粒子的飞行，同时，采用小生境技术，加入了部分变异和边界变异的机制，大大提高多目标优化解集合的分散性和均匀性［14］.

优化方法:在可行解目标空间随机均匀初始化粒子群，选取非劣解粒子作为精英集，通过小生境技术给精英集中的非劣解粒子分配适应度值，聚集程度越大的粒子适应度越小，精英集中第i个粒子的适应度为:

将适应度值最小的粒子作为精英集粒子群体历史最佳pg，按照公式(12)和(13)进行迭代.

3.3 本文算法步骤

粒子群多目标优化算法步骤如下:

第一步:设置参数，精英集规模E=100、小生境半径σ=0.48、加速因子 c1=c2=1.495、惯性因子 ω =0.729、调节参数α=1.2、最大周期值UC=260、最小周期值LC=80、最大迭代次数为50、选取粒子数为50.

第二步:令迭代次数变量NC=1，随机初始化粒子群，计算目标函数值，基于Pareto支配关系来选择个体历史最佳pi，筛选粒子中的非劣解作为精英集.

第三步:按(14)式计算精英集中个体的适应度.采用适应度值最小的粒子作为精英集中某次粒子迭代后的粒子群体历史最佳pg.

第四步:按式(12)和(13)更新粒子速度和位置(速度变化范围控制在［－1，1］，位置变化范围控制在［－5，5］).

第五步:计算各目标函数值，基于Pareto支配关系筛选出粒子群中非劣解，并加入精英集，同时删除劣解，形成新的精英集.

第六步:返回第三步计算新精英集中个体的适应度.若精英集中个体数超过最大容量，则按超出容量数的2倍选取适应度最小的个体，随机剔除其中50%;若粒子当前位置优于其历史最佳pi则替换pi，若粒子当前位置劣于pi则保持pi，若当前粒子无差别于 pi，则保持 pi.

第七步:令NC=NC+1，检查是否达到50次，若否，转步骤三继续.否则，输出精英集，即得到非劣解集，并结束运行.

4 实例应用

以长沙市某交叉口为背景交通流进行实例分析，该交叉口的各流向基本数据如表1，各个方向进口道均为一个左转车道、一个直行车道和一个右转车道，车道饱和流率取1500pcu/h.先根据基本数据来确定绿信比，然后运用粒子群多目标优化算法求解.

表1 交叉口各流向的基本数据

该交叉口的相位相序图，见图1:

图1 交叉口机动车与非机动车相位相序图

假设每辆公交车平均载客人数为35人，每辆小汽车平均载客为1.6人，每辆非机动车载客为1人.第一至第四相位的最小绿灯时间分别为18、16、18、16秒，总损失时间L为12秒，则最小周期应为80秒.根据本文提出的绿信比确定方法，当周期大于120秒时，则Δg＞0;周期小于120秒时，则Δg＜0;周期等于120秒时，则Δg=0.假设行人过街饱和流率为8人/s，到达率均为0.25人/s，行人相位最小绿灯时间均为16秒，共4个行人相位.

利用以上模型进行求解，下图2至图4为优解库中各目标函数对应周期时长的分布情况，可以看出各个目标函数与周期时长的变化趋势.图5为最优解前沿，取周期时长116秒作为结果应用(如表2)与其它方法对比.

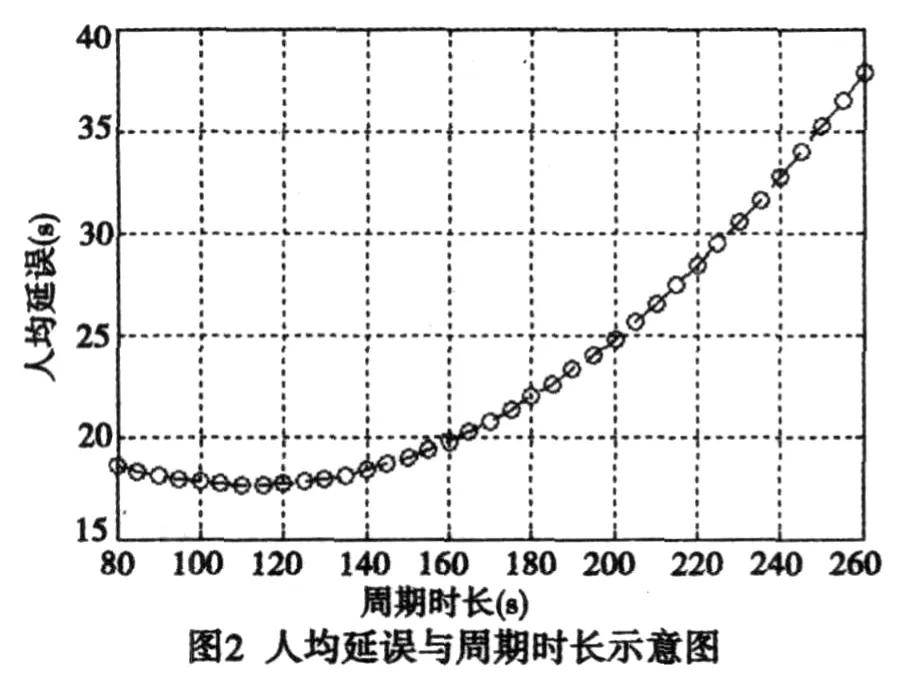
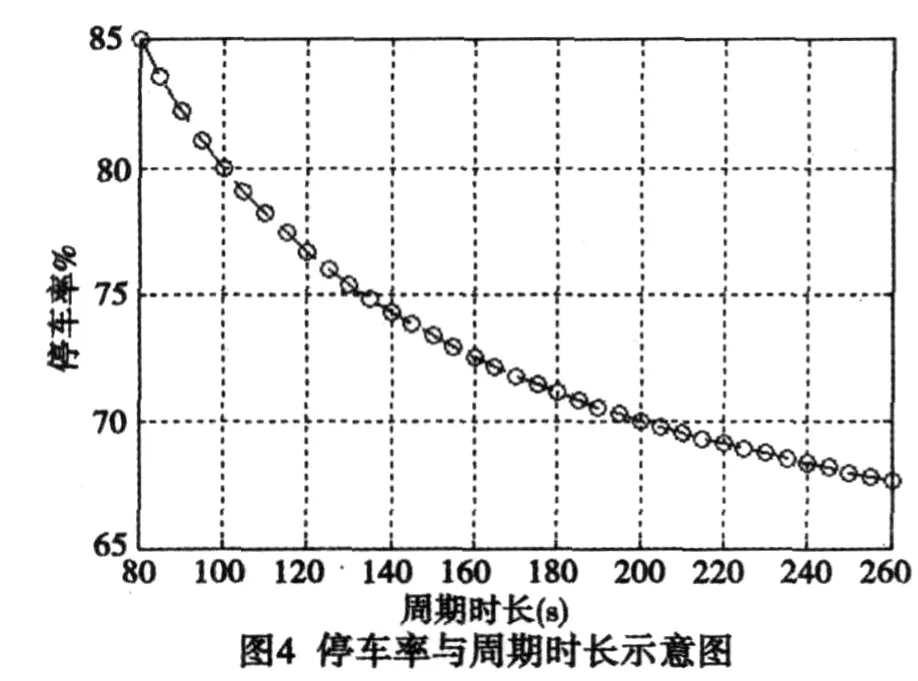
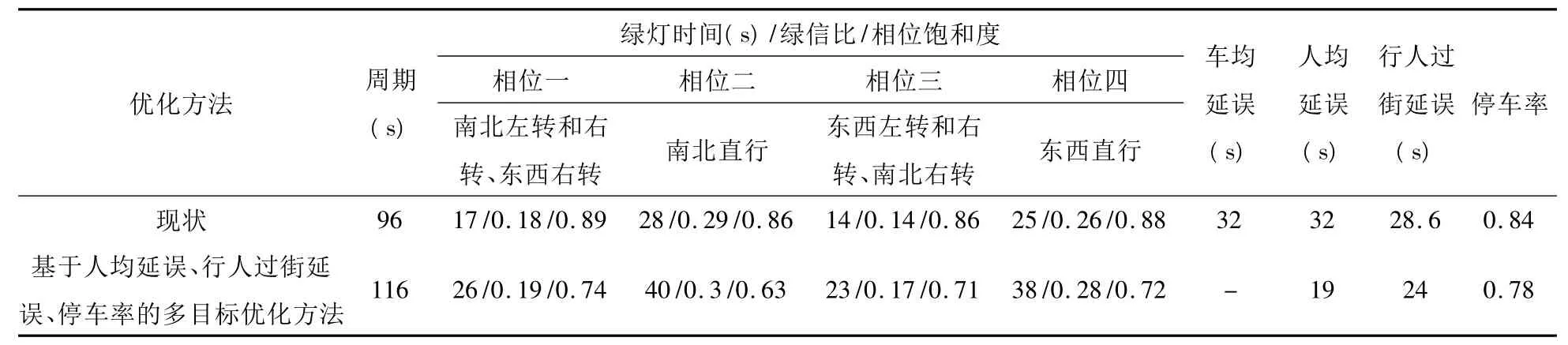
表2 两种多目标配时优化方法结果对比

显然，本文采用的多目标优化方法，人均延误降低了37.5%，行人平均延误和停车率也减少了.因此，在公共汽车和慢行交通构成比例较大的交叉口，应用基于人均延误、行人过街延误和停车率最小为目标的多目标优化方法，既能实现公共汽车优先通行，又能反映快、慢行交通的相互协调运行.

5 结语

本文针对公共汽车和慢行交通构成比例较大的信号控制交叉口，以人均延误、行人过街延误、停车率最小为目标，建立信号配时参数的多目标优化方法.首先以相位乘客流量比和相位饱和度优化绿信比，合理分配各个相位的绿灯时间.然后运用基于Pareto的多目标粒子群优化算法对模型进行求解.该方法明显降低了交叉口人均延误，体现了公共汽车优先通行，并没有对其它车辆造成负面影响.另外本文在建立人均延误模型时，将非机动车人均延误也计入其中，所以还能反映慢行交通与其它交通协调运行.但是本文计算是建立在相位相序已经优化好的条件下，所以存在一定的局限性，有待进一步研究.

［1］王正武，夏利民，罗大庸，等.单交叉口自适应公交优先控制［J］.中国公路学报，2010，(4):84 －90.

［2］Shalaby A，Lee J，Greenough J，et al.Development，evaluation，and selection of advanced transit signal priority concept directions［J］.Journal of Public Transportation，2006，(5):97 －120.

［3］张卫华，陆化普，石琴，等.公交优先的信号交叉口配时优化方法［J］.交通运输系统工程学报，2004，(3):49 －53.

［4］杨晓光，林瑜，杭明升，等.信号控制交叉口公共汽车优先信号确定方法研究［J］.中国公路学报，2001，(z1):101 －104.

［5］马莹莹，杨晓光，曾滢.信号控制交叉口周期时长多目标优化模型及求解［J］.同济大学学报，2009，(6):761 －765.

［6］陈小红，钱大琳，石冬花，等.基于慢行交通的交叉口信号配时多目标优化模型［J］.交通运输系统工程与信息，2011，(2):106－111.

［7］王秋平，谭学龙，张生瑞.城市单点交叉口信号配时优化［J］.交通运输工程学报，2006，(2):60 －64.

［8］Anderson J，Sayers T，Bell M.The objectives of traffic signal control［J］.Traffic Engineering Control，1998，(3):167.

［9］ Transportation Research Board.Highway Capacity Manual 2000［M］.Washington DC:National Research Council，2000.

［10］冯树民，裴玉龙.行人过街延误研究［J］.哈尔滨工业大学学报，2007，(4):613 －616.

［11］全永燊.城市交通控制［M］.北京:人民交通出版社，1989.

［12］Kennedy J，Eberhart R C.Swarm Intelligence［M］.San Francisco:Morgan Kaufmann Division of Academic Press，2001.

［13］李宁.粒子群优化算法的理论分析与应用研究［D］.武汉:华中科技大学博士学位论文，2006.

［14］Van Velduizen D A，Lamont G B.Multiobjective evolutionary algorithm test suites［A］.Proceedings of the 1999 ACM Symposium on Applied Computing［C］.San Antonio:ACM，1999.

U41

A

1008－4681(2012)02－0064－05

2012－03－01

李劲夫(1985－)，男，湖北咸宁人，长沙理工大学交通运输工程学院硕士生.研究方向:交通规划与设计.

(责任编校:晴川)