A Magnetic Induction Tomography System for Prospective Industrial Processing Applications

Hsin-Yu Wei and Manuchehr Soleimani*

Department of Electronic and Electrical Engineering, University of Bath, Bath, UK

A Magnetic Induction Tomography System for Prospective Industrial Processing Applications

Hsin-Yu Wei and Manuchehr Soleimani*

Department of Electronic and Electrical Engineering, University of Bath, Bath, UK

Magnetic induction tomography (MIT) is one of the newest industrial process imaging techniques. Main industrial applications of the MIT imaging are in high conductive flow imaging. However, recently it has been shown that the MIT may be useful for low conductive process imaging. This paper presents a cost effective hardware design for MIT in industrial applications, called Bath-MKI industrial MIT system. The system comprises 8 inductor coils and has the possibility of expansion to 16 coils. The excitation signals and the measured voltages are generated and measured using a LabView based system. Two 16 by 1 multiplexers are used to select between the coils. Measurements, excitation and multiplexing are all controlled by a National Instrument (NI) USB based DAQ:USB-6259 and a signal generator. Using the same electronics, the prototype is tested with two different coil arrays;one is a small scale ferrite core coil and one larger scale air cored coil. Experimental image reconstruction results are shown using both small scale and large scale coil arrays.

magnetic Induction tomography, coil sensors, forward problem, inverse solver

1 INTRODUCTION

Magnetic induction tomography (MIT) is a contactless electromagnetic imaging system. MIT has potential for use in many industrial and biological tomography applications [1].

MIT can image the spatial distribution of electrical conductivity and magnetic permeability within a region of interest. This is done by obtaining a set of measurements using inductive coils that are distributed around the periphery of the sample. Therefore, this form of tomography is non-intrusive and non-invasive,such that, the sensor coils are located external to the target. Systems typically operate by applying a set of interrogating field patterns to the region of interest(ROI) from different locations and directions. A number of measurements are taken by an array of sensors for each pattern. The measured data is then manipulated using mathematical inversion techniques to create an image of the internal object distribution. Areas of application for this technique include metal production,especially molten metal processes, and non-destructive testing [1-6]. Image resolution is low when compared with many forms of tomography because of the limited number of excitation and detection coils and the nature of low frequency electromagnetic fields in MIT.However, for some of these applications it is sufficient simply to identify highly conductive regions within the ROI, such as, whether a flow of molten steel is biased towards one side of a delivery nozzle or is evenly distributed over its cross-section. This paper presents a general overview of the MIT system, including electronics, sensor design and image reconstruction.

2 SYSTEM ELECTRONICS

ADG406 multiplexers (Analog Devices, Inc.) are employed in our system to accomplish the channel switching processes. ADG406 is a 16-to-1, monolithic CMOS analogue multiplexer which has features of low “ON” resistance and high input signal range. Its“break before made” feature also adds simplicity to the system. In our channel switching board, two multiplexers are utilised: one controls the transmitting channels, the other controls the receiving channels. All the corresponding multiplexer outputs are linked together, as shown in Fig. 1. For the system presented in this paper, only 8 multiplexer channels are connected to coils, however, one can easily utilise the system’s full capability if needed and expand the number of channels to 16.

Figure 1 ADG406 switching example, in this case, channel 0 is set to transmitting channel and the rest of the channels are reading the coil signal sequentially

For signal generation and data acquisition, a NI USB-6259 was used. USB-6259 contains 32 analog input channels and 4 analog output channels, which are capable of generating sinusoidal signals and reading thedetected signals from the coil sensor simultaneously. The DAQ card also has 48 bidirectional digital I/O which can be used to control our ADG406 multiplexers.

Figure 2 Block diagram of the small scale MIT system

Figure 3 Block diagram of the large scale MIT system

The in-built LabView functions are used to measure the amplitude changes of the detecting signals,which are the essential information required for image reconstruction. Fig. 2 shows a simplified system block diagram of the small scaled MIT system.

Our MIT system is a single frequency system.For the small scale system, the operating frequency is 5 kHz. With the NI LabView program and USB-6259,a 1.5V p-p, 5 kHz sinusoidal signals can easily be generated. The choice of signal strength is mainly based on the capabilities of the NI acquisition card,since USB-6259 analog outputs can only offer a maximum of 5 mA output current. For our large scale coil, since the sensor impedance is much lower at the same frequency (due to the removal of ferrite core),the USB-6259 can no longer provide enough current to the transmitting coil. In this case, the AC signal source is supplied by a TOPWARD 8112 signal generator instead. Fig. 3 shows the system block diagram of our large scale system. Fig. 4 shows a photo of the small scaled sensor array and the system electronics of the MIT system that was designed in this study.

3 COIL SENSOR DESIGN

3.1 Small scale sensor

Figure 4 Photograph of the small scaled MIT system and the arrangement of coil sensor arrays

The sensor array contains 8 off-the-shelf inductors(Murata Power Solutions, 2200 Series), which are equally spaced along the periphery of the object space being imaged. This particular inductor was chosen simply due to its availability. By selecting commercialized sensors, the consistency of the coil properties(size, inductance, number of turn etc.) can be predefined and standardized. Fig. 5 shows the structure of the ferrite cored inductor sensor, which has an inductance value of 4.7 mH. We suggest that any other coil which has a similar construction could also be used if required. It was realized in the previous proof of concept stage that these commercialized inductors do have capabilities of transmitting/detecting inductive signals, independently from the ferrite core material.The ROI is a circular object space with a diameter of 20 mm. The sensors are attached against the outer boundary of the measuring space; the distance between centers of two opposite coils is therefore 20 mm.

Figure 5 (a) Sensor array and (b) sensor structure: the left hand side shows the complete structure when the inductor casing is removed, the right hand side shows the shape of the ferrite core when the wire is removed

Figure 6 Photograph of the large scale MIT sensor array

3.2 Large scale sensor

The small scale sensor array described in the previous section was later expanded into a larger scale array to make the system more applicable to industrial applications. The new array is comprised again by eight coils. The air cored coil was manually wounded around a cylindrical plastic template with copper wire of 50 turns and has a radius of 21 mm. Same as the small scaled sensor, this hand wound coil may act either a transmitter or a receiver, as determined by the PC controlled multiplexer. The sensors are placed equally at the periphery of a circular wooden base,thus creating an interaction angle of 45 degrees between adjacent coils for our eight channel system. The circular region for our MIT system is a circular space enclosed by coil arrays, with a diameter of 110 mm.Fig. 6 shows a diagram of the coil array of the large scale coil sensor array.

4 IMAGE RECONSTRUCTION SOFTWARE

The forward problem in MIT is a classical eddy current problem. This problem can be formulated in terms of the magnetic vector potential A for the sinusoidal waveform excitation case using complex phasor notation:

where σ is electrical conductivity, μ is magnetic permeability and Jsis the applied current density in an excitation coil. In this study we used a so called A, A formulation for the eddy current problem, and for that we have to mesh the coils as part of discretisation of the domain [7]. If the total current in the excitation coil is I0, the sensitivity of the induced voltage to the conductivity is [2, 3, 5]

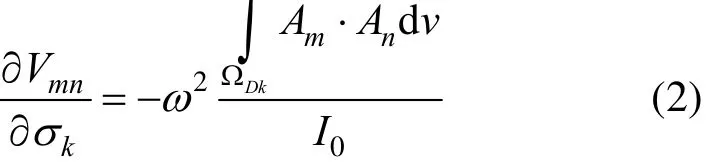
where Vmnis the measured voltage, σkis the conductivity of pixel k, ΩDkis the volume of the perturbation(pixel k), Amand Anare respectively solutions of the forward solver when excitation coil (m) is excited by I0and sensing coil (n) is excited with unity current.

In image reconstruction, only linear algorithm is considered because of its simplicity and less computational cost is required, as it can be achieved through the matrix multiplications. The linear method was based on Tikhonov regularization [8], which uses a universal regularization technique for solving the ill-posed inverse problem in the following manner:

where x is the image pixel vector, z is the measurement vector, J is the sensitivity matrix (Jacobian matrix), I is an identity matrix and μ is the regularization parameter. In this single-step algorithm, sensitivity matrix, J,was obtained with a direct measurement method [5].

5 IMAGING RESULT

For the selected operating frequency (kHz ranges),the target measuring materials should be metallic objects because the operating frequency is not high enough to detect biological tissue, which has conductivity of several orders in magnitude lower than metals.

5.1 Small scale system

In this experiment, all the testing objects were tensile steel screws, with cross sections of 5 mm diameter, as shown in Fig. 7 (a). The screws were placed within the measuring space, and the image reconstruction work was done in MATLAB. Fig. 7 shows the images result by using the reconstruction algorithm discussed in the previous section. The regularization parameter was selected based on the L-curve method throughout all the imaging experiments for the best image performance [4].

Figure 7 (a) Location of the 5 mm screws within the measuring space using small ferrite cored array, and (b)corresponding images by using the Tikhonov regularization algorithm

The screws were moved into various locations within the measuring space for image reconstruction tests. In the single object case, it can be seen that the 5 mm screw can be clearly identified at the centre of the reconstructed image. In the dual-object case, two iron screws were placed roughly 6 mm apart, which can also be distinguished in the image. Similar tests were done for both 3 screws and 4 screws cases; it has been shown that the targets were clearly visible at the correct positions in the images.

The result images are satisfactory. However, the sizes of the imaging objects were considered to be large if comparing the screw size to the measuring space (6% of the measuring area). To further demonstrate the system’s ability of metal detection, the similar tests were conducted in the large scale system,whose result will be shown in Section 5.2.

5.2 Large scale system

Similar experiments were conducted with the larger sensor array. But this time different sized steel screws were used to further illustrate the system capability of identifying high conductivity objects in the reconstructed images. The diameters of the screws were 5 mm, 8 mm and 19 mm respectively. Fig. 8 shows the images result.

The reconstructed image results again show the system’s ability of detecting high conductivity objects.The system with air cored coil sensors can also provide satisfactory images as they successfully distinguish the screws with different sizes. With its capability of detecting the 5 mm diameter screw (roughly 0.2% of the measuring area), an application on metallic object detection in food, pharmaceutical and packaging industry can also be suggested. As in these industries, a complete elimination of metal contamination from their end product is compulsory, in order to comply with the health and safety regulations.

In both the result sections (5.1 and 5.2), it is worth noticing that all the images provide a rather“dispersed” result, i.e. the reconstructed conductivity distributions are smooth and varied slowly compare to the sharp and distinct contract in the real situation(metal screw and free space). This is the effect from the Tikhonov regularization that is introduced in the inverse solver. Regularization plays an important role in the image reconstruction process as it not only improves the conditioning of the problem, but also makes the images more resistive to the hardware noise.

6 CONCLUSIONS

Figure 8 (a) Location of the different sizes screws within the measuring space using large air cored array, and (b)corresponding images by using the Tikhonov regularization algorithm

Our MIT system here is a cost effective system,which has a capability to image metallic structures.This study has shown detailed information on a simple MIT system for imaging metallic objects. The use of the NI-DAQ card simplifies the system design significantly.Both commercialized inductor sensors and hand wounded coils have the capabilities being transmitter/receiver of MIT systems. Example images have been presented, which show that it is possible to image simple high conductivity structures using an 8-coil array, operating at a single excitation frequency. These encouraging results indicate the possibility of applying MIT into various industrial applications, such as metal detection in food industry and molten metal flow imaging.

1 Ma, X., Peyton, A.J., Binns, R., Higson, S.R., “Electromagnetic techniques for imaging the cross-section distribution of molten steel flow in the continuous casting nozzle”, IEEE Sensors J., 5 (2),224-232 (2005).

2 Dyck, D.N., Lowther, D.A., Freeman, E.M., “A method of computing the sensitivity of the electromagnetic quantities to changes in the material and sources”, IEEE Trans. Magnet., 3 (5), 3415-3418(1994).

3 Scharfetter, H., Riu, P., Populo, M., Rosell, J., “Sensitivity maps for low-contrast-perturbations within conducting background in magnetic induction tomography (MIT)”, Physiol. Meas., 23, 195-202(2002).

4 Ma, X., Peyton, A.J., Higson, S.R., Lyons, A., Dickinson, S.J.,“Hardware and software design for an electromagnetic induction tomography (EMT) system for high contrast metal process applications”, Meas. Sci. Technol., 17, 111-118 (2006).

5 Soleimani, M., Lionheart, W.R.B., Peyton, A.J., Ma, X., “A 3D inverse finite element technique applied to experimental magnetic induction tomography data”, In: 4th World Congress on Industrial Process Tomography, Aizu, Japan (2005).

6 Soleimani, M., Lionheart, W.R.B., “Image reconstruction in three-dimensional magnetostatic permeability tomography”, IEEE Trans. Magnet., 41 (4), 1274-1279 (2005).

7 Soleimani, M., “Sensitivity maps in three-dimensional magnetic induction tomography”, Insight, 48 (1), 39-44 (2006).

8 Calvetti, D., Morigi, S., Reichel, L., Sgallari, F., “Tikhonov regularization and the L-curve for large discrete ill-posed problems”, J.Comput. Appl. Math., 123, 423-446 (2000).

2011-11-17, accepted 2012-01-10.

* To whom correspondence should be addressed. E-mail: m.soleimani@bath.ac.uk