梯度复合材料热应力影响因素正交有限元分析

范世通，汤海波，张述泉，王华明

（北京航空航天大学 材料科学与工程学院大型整体金属构件激光直接制造教育部工程研究中心，北京100191）

梯度复合材料热应力影响因素正交有限元分析

范世通，汤海波，张述泉，王华明

（北京航空航天大学 材料科学与工程学院大型整体金属构件激光直接制造教育部工程研究中心，北京100191）

为了分析梯度层厚度、梯度层组成相体积分数及组成相长径比三种因素对热应力的影响，建立了梯度复合材料的物理模型，并采用有限元分析方法计算了该模型冷却至室温的热应力，同时使用正交设计对各因素的重要程度进行了数量估计。结果表明：三种因素中梯度层厚度对热应力的影响最为显著，次之为组成相体积分数，而长径比的影响较小。

梯度材料；热应力；有限元分析

梯度材料作为一种材料设计的概念，是由日本科学家在20世纪80年代中期提出来的，旨在满足航天、国防等高新技术领域对材料提出的苛刻要求［1］。最早的功能梯度材料一面为耐高温的陶瓷，另一面为高温合金，中间层为陶瓷相与金属相混合的梯度层。这种在材料的制备过程中通过连续控制材料的微观要素，使其组织及成分呈梯度分布，制备出内部无明显界面［2］的梯度复合材料的理念能极大地缓解高温条件下陶瓷和金属间由于热物理性能不匹配而产生的热应力。目前，梯度材料已经扩展到多种材料体系，在众多的工程领域中都具有广阔的应用前景。

针对梯度材料结构的设计，国内外学者展开了大量的研究。而将有关材料理论与计算机数值模拟相结合的方法也是大多数学者分析梯度材料热应力问题的有效方法之一。对于梯度材料热应力数值模拟的报道，大多通过从宏观角度控制梯度层层数、厚度和梯度分布指数来缓和应力并使其达到合理分布［3－10］，而有关梯度层中组成相的形态对梯度材料热应力影响的研究报道较少。事实上，梯度层组成相的形态直接影响梯度层的性能，对梯度材料热应力的影响也不容忽视。同时，虽然梯度材料各因素对热应力的影响规律均有报道，但就各因素影响的显著性却分析很少。

本工作采用正交设计方法，利用有限元综合分析了梯度层厚度、组成相体积分数及组成相形态三种因素对梯度材料热应力的影响，重点考察三种因素对梯度材料热应力影响的显著性，为梯度材料的设计和优化提供借鉴。

1 模型的建立

1.1 几何模型及边界条件

图1为梯度复合材料几何模型及其圆截面示意图。样品尺寸为φ15mm×5mm，沿Z轴正方向分别为纯材料层M、梯度层G和纯材料层R，图1（a）中，tG为梯度层厚度。梯度层由组成相R和基体相M组成，其中组成相R的形态为长径比为l／d的短棒状，体积分数为VR，其分布如图1（b）所示，随机分布。计算的边界条件为材料的初始参考温度500℃，置于室温环境冷却至25℃，环境对流系数为110W／（m2·℃），设定该过程为稳态过程。

图1 梯度复合材料几何模型（a）及梯度层圆截面示意图（b）Fig.1 Geometry model（a）and scheme of circular section of gradient composite geometry model（b）

1.2 材料物理性能及热应力影响因素正交设计

稳态热应力的计算是热－结构耦合场问题，该问题的数值模拟需要输入材料的弹性模量E、线膨胀系数α、热导率k及泊松比μ。梯度层的热导率k和泊松比μ采用线性混合规则计算，线膨胀系数α采用改进后的复合材料混合法则［11］计算（式（1））。而弹性模量E，由于组成相长径比较小，相对于长度方向，其端面与基体的端面效应不能忽视，因而采用简单的混合法则计算梯度复合材料的弹性模量E将会产生较大的误差，而 Halpin－Tsai Equations［12］考虑了增强相长度对弹性模量的影响，其结果更为精确，故采用Halpin－Tsai Equations计算梯度复合材料的纵向弹性模量E1和横向弹性模量E2，如式（2），（3）所示。由于组成相R随机均匀地分布在各向同性的均质基体M中，且仅考虑两相的热弹性问题，可简化梯度层为各向同性材料，其总体弹性模量E采用式（4）所示的半经验公式计算得到。

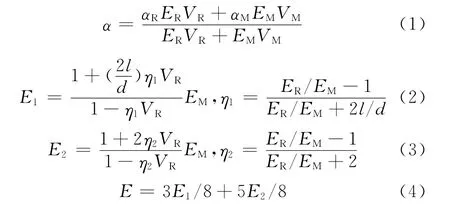
式中：α，αM，αR分别为梯度层、M相和R相线膨胀系数；E，E1，E2，EM和ER分别为梯度层、纵向、横向、M相和R相弹性模量；η1，η2分别为纵向和横向增强作用参数。

由于W，Cu的热膨胀系数和弹性模量等物理性能差别悬殊，由这两种材料组成的复合材料热应力必然显著，而W－Cu复合材料在热沉材料［13］上有广泛的应用且可望用作偏滤器材料［14］，因而本工作采用 W，Cu的物理性能数据分别作为组成相R和基体相M进行计算，不仅能更清晰地反映梯度材料梯度层厚度、组成相体积分数和形态三种因素对梯度复合材料热应力的影响，同时也具有一定的现实意义。表1为组成相R和基体相M的物理性能数据。

表1 模拟梯度材料R和M两组成相的常规性能Table 1 Conventional properties of R and M for simulation

对R／M梯度材料梯度层厚度、梯度层组成相R体积分数及长径比三种影响因素采用正交设计取五个水平进行热应力有限元分析，采用L25（56）正交表［15］，三种因素的取值如表2所示。

2 正交有限元分析结果及讨论

2.1 最大Mises等效热应力分布

控制热应力使之合理分布对工件性能和使用寿命有着重要的实际意义。本工作建立的模型Mises等效热应力的分布主要受体积分数的影响，如图2所示，MX，MN分别为Mises等效热应力最大和最小值，随体积分数的增加，最大Mises等效热应力的位置逐渐由R层与梯度层界面处过渡到梯度层与M层界面。针对不同考察因素的计算结果，取该两处中最大Mises等效热应力，作为评判三种因素对热应力显著性影响的标准。

表2 三种因素的取值Table 2 Value of the three factors

图2 梯度层组成相R不同体积分数的梯度材料热应力分布云图（a）体积分数为20%；（b）体积分数为60%Fig.2 Stress cloud charts of gradient composites withdifferent volume fraction of R in the graded layer（a）20%volume fraction；（b）60%volume fraction

2.2 三种因素对热应力的影响规律及显著性分析

正交试验设计的方差分析通过提供一个标准来考察、判断因素对实验结果的影响是否显著，可以对影响实验结果的各因素的重要程度给出精确的数量估计。本工作在显著性水平α＝0.005下，采用F检验三种因素对最大Mises等效热应力的影响进行显著性分析。若计算出的统计量观测值F因≥F1－α（f因，fe）（F1－α为F分布显著性水平α下1－α分位点，f因，fe分别为因素和误差的自由度），且F因越大，则以显著性水平α判断此因素对实验结果的影响越显著，否则判断此因素对实验结果的影响不显著。经计算，梯度层厚度、组成相R的体积分数及组成相长径比三种因素的观测值F因分别为23.9，4.18，0.64，而F1－α（f因，fe）（f因＝4，fe＝16）为3.01。这表明梯度层厚度对热应力的影响非常显著，体积分数的影响也很显著，而组成相长径比的影响不显著。

图3为梯度层组成相R不同体积分数的梯度复合材料热应力随梯度层厚度变化曲线，可见，梯度层厚度对热应力的影响非常显著。当梯度层厚度较小时，梯度层组成相体积分数越大热应力越小。随梯度层厚度增加热应力总体呈减小趋势，而不同组成相体积分数对热应力的影响不同，随体积分数的增大热应力减小趋势呈先增大后减小的趋势，体积分数为60%的材料热应力甚至有小幅增大趋势，其结果是当梯度层厚度为4mm时，梯度层体积分数为60%，10%的热应力最大。

图3 组成相R不同体积分数和梯度层厚度对梯度复合材料热应力的影响Fig.3 Effect of volume fraction of R and graded layer thickness on thermal stress of gradient composites

由以上分析可知，梯度层组成相长径比对热应力的影响是不显著的。为考察其具体影响规律及大小，选取如图3所示对热应力影响效果最差的梯度层厚度为0.5mm、组成相体积分数为10%的模型，对不同长径比的梯度复合材料进行有限元分析，其结果如图4所示，可知，随长径比增加，梯度复合材料的热应力是逐渐增大的，但相对于梯度层厚度及组成相体积分数的影响而言长径比对热应力的影响很小。

2.3 三种因素最优选择

以热应力越小越好为标准，根据正交设计的方差分析，依据各因素的显著性选取热应力的平均值最小的水平，即可确定最优实验方案。表3为三因素五种水平最大Mises等效热应力平均值，可知，梯度层厚度、梯度层组成相R体积分数及组成相长径比分别选取5号，2号，1号水平时材料热应力最小，即本工作所建模型的最优方案是梯度层厚度为4mm，梯度层组成相体积分数为20%、长径比为3。该方案并不包含在正交表中已做过的25个实验方案之中，经有限元计算验证发现，梯度层厚度为4mm，梯度层组成相体积分数为20%、长径比为3的梯度复合材料其最大Mises等效热应力为27MPa，较之于图3中所示正交试验方案中最小热应力27.5MPa更小，较之于两种材料直接连接不含梯度层的材料的热应力78.7MPa降低了65.7%。说明，采用正交设计方法是有效的，也充分体现了正交设计的优越性。

图4 梯度层厚度为0.5mm、组成相R体积分数为10%时长径比对最大Mises等效热应力的影响Fig.4 Effect of aspect ratio on the maximum Mises thermal stress with graded layer thickness of 5mm and 10%volume fraction

表3 三因素五水平最大Mises等效热应力均值（MPa）Table 3 Average value of maximum Mises thermal stress of factors with five different levels（MPa）

3 结论

（1）梯度层厚度、梯度层组成相体积分数对梯度复合材料热应力有显著的影响，梯度层厚度的影响尤为显著，而梯度层组成相长径比的影响较小。

（2）梯度复合材料热应力随梯度层厚度增加总体呈减小趋势，不同组成相体积分数对热应力减小趋势的影响不同，随体积分数的增大热应力减小趋势呈先增大后减小的趋势。

（3）可以通过正交有限元设计得出使热应力最小的最优方案，针对本工作所建W－Cu梯度复合材料模型，该最优方案为梯度层厚度为4mm，梯度层组成相体积分数为20%，长径比为3。

［1］ 仲政，吴林志，陈伟球.功能梯度材料与结构的若干力学问题研究进展［J］.力学进展，2010，40（5）：528－535.

［2］ 朱信华，孟中岩.梯度功能材料的研究现状与展望［J］.功能材料，1998，29（2）：121－127.

［3］ DELFOSSE D，CHERRADI N，ILSCHNER B.Numerical and experimental determination of residual stresses in graded materials［J］.Composites Part B：Engineering，1997，28（1－2）：127－141.

［4］ WILLIAMSON R L，RABIN B H，DRAKE J T.Finite element analysis of thermal residual stresses at graded ceramic－metal interfaces.Part 1.Model description and geometrical effects［J］.Journal of Applied Physics，1993，74（2）：1310－1320.

［5］ CHEN Fu－yi，JIE Wan－qi.Finite element design of MgO／Ni system functionally graded materials［J］.Journal of Materials Processing Technology，2007，182（1－3）：181－184.

［6］ 张国兵，郭全贵，刘朗，等.圆板状SiC／C功能梯度材料残余热应力特征有限元分析［J］.功能材料，2007，38（7）：1102－1104.

［7］ CAO Pin－lu，LIU Bao－chang，YIN Kun，et al.Optimization design and residual thermal stress analysis of PDC functionally graded materials［J］.J Zhejiang Univ Science A，2006，7（8）：1318－1323.

［8］ JIN Gang，AWAJI HIDEO.Residual thermal stresses in multilayered functionally graded material plate［J］.Materials Science Research International，2003，9（2）：125－130.

［9］ 陶光勇，郑子樵，刘孙和.W／Cu梯度功能材料板稳态热应力分析［J］.中国有色金属学报，2006，16（4）：694－700.

［10］ LIEW K M，KIRIPORNCHAI S，ZHANG X Z，et al.Analysis of the thermal stress behavior of functionally graded hollow circular cylinders［J］.International Journal of Solids and Structures，2003，40（10）：2355－2380.

［11］ 陈烈民，杨宝宁.复合材料的力学分析［M］.北京：中国科技出版社，2006.

［12］ HALPIN J C，KARDOS J L.The Halpin－Tsai equations：a review［J］.Polymer Engineering and Science，1976，16（5）：344－352.

［13］ 刘彬彬，谢建新.W－Cu梯度热沉材料的成分与结构设计［J］.稀有金属，2005，29（5）：757－761.

［14］ 凌云汉，白新德，李江涛，等.W／Cu功能梯度材料的热应力优化设计［J］.稀有金属材料与工程，2003，32（12）：976－980.

［15］ 韩於羹.应用数理统计［M］.北京：北京航空航天大学出版社，2006.

Finite Element Analysis of Factors to Thermal Stress in Gradient Composite with Orthogonal Method

FAN Shi－tong，TANG Hai－bo，ZHANG Shu－quan，WANG Hua－ming
（Engineering Research Center on Laser Direct Manufacturing for Large Metallic Components（Ministry of Education），School of Materials Science and Engineering，Beihang University，Beijing 100191，China）

In order to analysis the contributions of graded layer thickness，constituent phase volume fraction and aspect ratio to the being of thermal stress，physical models of gradient composite were established.The thermal stresses of the models induced by cooling to room temperature were simulated using finite element method，and the importance of the factors was mathematically estimated by orthogonal design method.The results show that，in the three factors，graded layer thickness has the most remarkable effect to thermal stress，and the influence of constituent phase volume fraction is obvious，but the effect of aspect ratio is not significant.

graded material；thermal stress；finite element method

TB33

A

1001－4381（2012）08－0001－04

国家重点基础研究发展计划（973计划）资助项目（2010CB731705）

2011－02－17；

2012－01－25

范世通（1985－），男，硕士研究生，从事梯度复合材料方面研究工作，联系地址：北京市海淀区学院路37号北京航空航天大学4＃208激光实验室（100191），E－mail：fanstone2001＠yahoo.com.cn