符号模式矩阵的幂等性质

朱兴文 王彭德

（大理学院，大理 671003）

符号模式矩阵的幂等性质

朱兴文 王彭德

（大理学院，大理 671003）

通过对符号模式矩阵的研究，给出了具有frobenius型的符号模式矩阵中上三角块的形式，及一种构造幂等的方法，研究符号模式矩阵的符号幂等与允许幂等的关系。

符号模式矩阵；符号幂等；允许幂等

符号模式矩阵是指矩阵中的元素取值于集合{0，+，－}的矩阵。给定实矩阵 B，sgn(B)表示与矩阵 B的符号相同的符号模式矩阵。所有n×n的符号模式矩阵构成的集合用Qn表示。对于一个n×n符号模式矩阵A，有一个实矩阵的类，其中的矩阵的元素与A有相同的符号，这样就有n×n符号模式矩阵A的一个定性矩阵类，记为

若A是一个实m×n矩阵，则A同样可以决定一个定性矩阵类［1］，记为

单位符号模式矩阵是将单位数字矩阵中的1用+代替所得到的符号模式矩阵，用In表示n×n的单位符号模式矩阵。置换模式矩阵P是指一个n阶符号模式矩阵P，若它的每一行和每一列上只有一个元素等于+，而其余元素都等于0，则称P为置换模式矩阵［2］。矩阵A,B是置换相似是指存在置换模式矩阵P使得B=PAPT［2］。符号模式的强迫性是指如果P是实矩阵对应的某一个性质，一个符号模式矩阵A强迫性质P是指对于任意的实矩阵B∈Q(A)都有这个性质P。符号模式的允许性是指如果P是实矩阵对应的某一个性质，则称一个符号模式矩阵A允许性质P是指存在实矩阵B∈Q(A)有这个性质 P［4］。

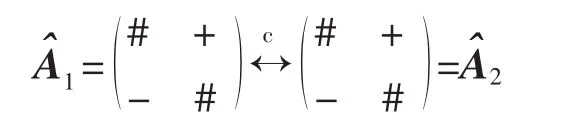
符号幂等A是指一个n×n的符号模式矩阵，若对任意 B∈Q(A)，B2∈Q(A)，则称 A是符号幂等的。符号模式矩阵的运算，即A2=A，称A是符号幂等的符号模式矩阵。允许幂等A是指一个n×n的符号模式矩阵，若存在B∈Q(A)，B2=B，则称A是允许幂等的［4］。 例如：

通过计算可得B2=B，所以B是符号幂等的，即A∈SI。对于符号模式矩阵B，能找到一个与B符号相同的实矩阵C，如：

使得C2=C，所以符号模式矩阵C是允许幂等的，即B∈ID。

1 引 理

引理1［5］A是可约的n×n的符号模式矩阵，则A可置换相似为Frobenius标准型，即

其中Aii是完全为零或正的方阵（包括一阶零矩阵），i=1,2,…,k。

引理2［3］符号模式矩阵的符号幂等及允许幂等在以下变换下是封闭的：

（1）符号差相似；

（2）置换相似；

（3）转置。

2 非负符号模式矩阵的幂等性

下面先来讨论非负符号模式矩阵的幂等性，对于非负符号模式矩阵的幂等性，黄荣给出了允许幂等的刻划［5-6］，非负符号模式矩阵是指元素取自{0,+}的符号模式矩阵，非负符号模式矩阵在矩阵的运算过程中不会出现除非负元素外的其他元素。

定理1［6］设A是一个n阶非负符号模式矩阵，则A是符号幂等的充分必要条件是A允许幂等。

根据定理1，可以知道在非负符号模式矩阵中，只要一个符号模式矩阵A是符号幂等的，那么它就是允许幂等的，所以下面只对非负符号模式矩阵的符号幂等性进行研究。

对于非负符号模式矩阵的幂等性研究，先从不可约的非负符号模式矩阵开始研究。对于非负符号模式矩阵，如果n×n符号模式矩阵A的元素aij＞0，符号模式矩阵A必然是符号幂等的，同样，A也是允许幂等的。

定理2［6］设符号模式矩阵A是一个不可约的n阶非负符号模式矩阵，则A符号幂等的充分必要条件是 A＞0或A=0。

对于一个n阶符号模式矩阵A，如果A是可约的，则存在n阶置换符号模式矩阵A，使得

其中：B,D是非零方阵，则A是可约符号模式矩阵［1］。又根据引理1，可约符号模式矩阵可置换相似为Frobeniu 标准型为［5］：

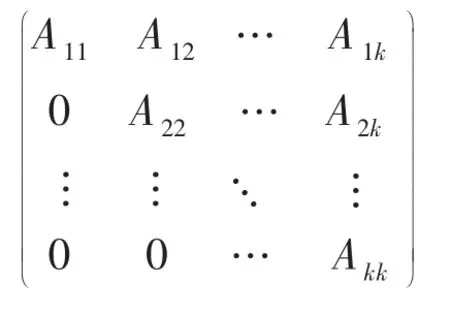
由于Frobeniu标准型是上三角符号模式矩阵，根据引理 2，只要研究所有的 i＜j(i,j=1,2,…,k)的矩阵块的幂等关系就能反映出原矩阵的幂等性。如果可约符号模式矩阵A是符号幂等的，那么A的Frobeniu标准型中的Aij也是符号幂等的，即A2ij=Aij，对于非负符号模式矩阵而言，由定理2可知Aij≥0。

定理3 设A是一个n阶可约非负符号幂等模式矩阵，它的Frobenius标准型为：

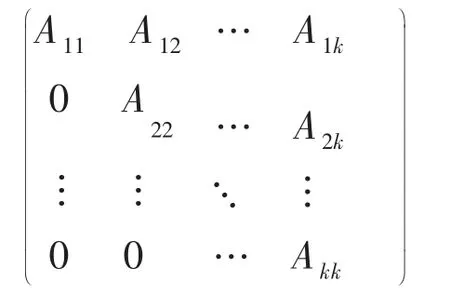
若 Aii＞0(i=1,2,…,k)，则对任意 i＜j，Aii＞0 或 Aii=0。

证明：（反证法）假设存在 Aii(i＜j)，且 Aii中既有零元又有非零元，同时，不妨设Aii的第i行第j列元素为零，因为A2=A，矩阵A2也能置换相似为Frobenius标准型，且其第i行第j列的方阵与Aii相等，则Aij可表示为

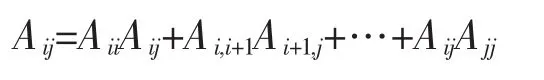
由于Aij的第i行第j列的元素aij为零，可知上式的任意两项的和，都有第i行第j列的元素为零，不妨取 AiiAij+AijAjj， 可知 aij=aiiaij+ai，i+1ai+1，j+…+aijajj=0其中 aii,ai,i+1,…,aij为Aii中的非零元素，aij,ai+1,i,…,ajj为Aij的非零元素，且

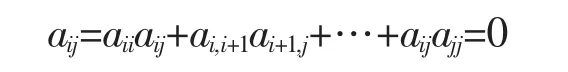
其中：aii,ai,i+1,…,aij为Aij的非零元素，aij,ai+1，j,…,ajj为Ajj中的非零元素，由题设，Aii,Ajj＞0，可得Aij的第i行和第j列全为零。同理可知Aij=0，即Aij为零方阵，与假设矛盾，定理得证。

接下来，可以构造一个n阶可约非负符号幂等模式矩阵：

根据定理3，令k=n，Aij为一阶矩阵，则当aii＞0(i=1,2，…，n)，对任意 i＜j，aij＞0 或 aij=0。

反过来，若 aij≥0(i＜j)，可得 aii≥0，可以推导出符号幂等的充分必要条件如下：

定理4 设

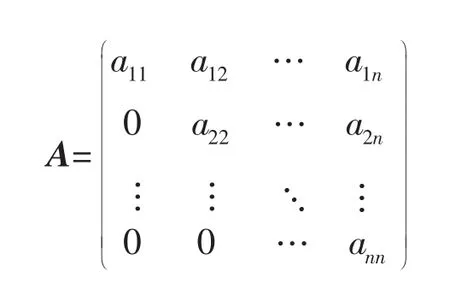
是一个n阶可约非负符号模式矩阵，则A符号幂等的充分必要条件为：

对任意 i＜j，有 aij＞0 或 aij=0，且满足：

（1）若存在 1≤s＜t＜n，使得对任意 s≤i＜t，有 aii=0，则对任意 s≤i＜j≤t，有 aij=0；

（2）若存在 1≤s＜t≤n，使得 ast=0，则对任意 s≤p≤t，有 aspapt=0。

证明：充分性是显然的，下面证明必要性。（1）由已知得：对任意 s≤i＜t，有 aii=0则(A2)i,i+1=aiiai,i+1+ai,i+1ai+1,i+1=0

因为A2=A，所以对任意 s≤i＜t，有(A2)i,i+1=ai,i+1=0，又因为

(A2)i,i+2=aiiai,i+2+ai,i+1ai+1,i+2+ai,i+2ai+2,i+2=0， 同理由A2=A，对任意 s≤i＜t，有(A2)i,i+2=ai,i+2=0，类似可证，对任意s≤i＜j≤t，有 aij=0。

（2）因为A2=A，由 ast=0，有(A2)st=0，即(A2)st=assast+as,s+1as+1,t+…+astatt=0，因为A为非负符号模式矩阵，所以有

assast=as,s+1as+1,t=…=astatt=0，所以，对任意 s≤p≤t有aspapt=0。

根据以上结论，可以构造一个符号幂等的符号模式矩阵，例：设n=5,s=2,t=4，可以构造一个5阶的符号模式矩阵A如下：易证A符号幂等的。

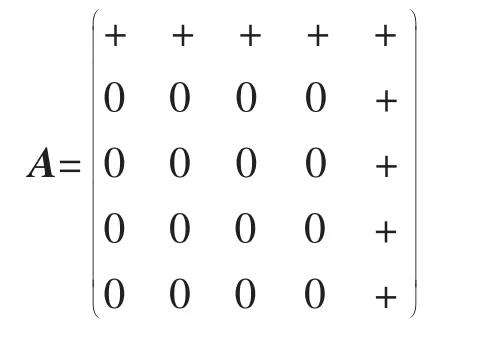
根据引理1，若n阶可约符号模式矩阵

那么A能置换相似为Frobenius标准型

根据定理4的结论，可推导出以下结论：

定理5 设A是n阶可约非负符号模式矩阵，它的Frobenius标准型为

则A符号幂等的充分必要条件为：

对任意 i＜j，有 Aij＞0 或 Aij=0，且满足

（1）若存在 1≤s＜t≤n，使得对任意 s≤i≤t，有Aij=0，则对任意 s≤i＜j≤t有 Aij=0。

（2）若存在 1≤s＜t≤n，使得 Ast=0，则对任意 s≤p≤t，有 AspApt=0。

证明：略。

3 符号模式矩阵符号幂等与允许幂等的关系

在文献［4］中，我们知道：若一个方的非负符号模式矩阵A是允许幂等的，则A是符号幂等的。然而，对一般的n×n允许幂等的符号模式矩阵A，我们却不能得出A是符号幂等的。这是因为在A2的运算中会出现#元素，所以我们得到的是A2与A是相容的，即 A2↔cA。例如：有B=B2，所以A是允许幂等的，但A不是符号幂等的。

由于A2运算中的#元素，文献［3］中指出对一般符号模式矩阵是不成立的。

现在，我们来考虑这个问题的反面。很显然，对一般情况而言，它也是不成立的。例如：是符号幂等的，但我们找不到任何的实矩阵B∈Q(A)使得B=B2，即：A是符号幂等的，但A是允许幂等的。在文献 ［3］、［4］ 和 ［6］中，已经给出了一些关于符号幂等与允许幂等的结论，特别是在文献［6］中，作者得出了一些关于非负符号模式矩阵幂等的等价命题。

定理6 如果符号模式矩阵A是允许幂等的,且在A2的运算中没有出现#元素，那么A是符号幂等的,且A的主对角线上的元素为非负元素。

证明：由于A是允许幂等的，所以A2↔cA，又因为在A2的运算中没有出现 #元素,故A是符号幂

等的。根据引理1，A可广义置换相似于

其中Aii是方的全正或者全为零的符号模式矩阵，i=1,2,…,k。故存在置换符号模式矩阵P使得A=PTBP。由于在进行广义置换相似的过程中，A的主对角元素的符号并不会发生变化，只是位置顺序发生变化。所以A的主对角元素的符号与B的主对角元素的符号相同，从而，根据B的主对角元素的符号，我们可以得出A的主对角线上的元素为非负元素。

定理7 设A是n×n可约符号模式矩阵，若存在n阶置换符号模式矩阵S，使得B=STAS为非负符号幂等模式矩阵，则A是允许幂等的。

证明：因为B=STAS为非负符号模式矩阵，且B是符号幂等的，由定理1知B是允许幂等的，所以，存在实矩阵C∈Q(B)，令C2=C。从而，存在实矩阵S′∈Q(S)，使得 S′CS′T∈Q(A)，有(S′CS′T)2=S′C2S′T=S′CS′T，所以，A允许幂等。

定理8 设A为n阶可约符号幂等模式矩阵，它的Frobenius标准型为

其对角块不存在零元，若存在n阶置换矩阵S，使得B=STAS为非负符号幂等模式矩阵，则A是允许幂等的。

[1]Brualdi R A，Shader B I.Matrices of Sign-solvable Linear Systems[M].Cambridge:Cambridge University Press,1995.

[2]Hall F J,Li Z.Sign Pattern Matrices[M].Handbook of Linear Algebra Simon and Hall/CRC Press,Boca Raton,FL.2007.Chapter33.

[3]Frank J Hall,Zhongshan Li,Bhaskara Rao.From Boolean to Sign Pattern Matrices[J].Linear Algebra and Its Applications，2004，393:233-251.

[4]Eschenbach C A.Idempotence for Sign Pattern Matrices[J].Lin.Alg.Appl.1993，80:153-165.

[5]黄荣.矩阵的Hadamard积与符号模式[D].武汉：华中师范大学，2008.

[6]Rong Huang.Sign Idempotent Sign Patterns Similar to Nonnegative Sign Patterns[J].Lin.Alg.Appl.2008，428:2524-2535.

The Idempotent Properties of Sign Pattern Matrices

ZHU Xingwen WANG Pengde
(Dali University,Dali 671003)

We investigated the properties of sign pattern matrices,giving the form of upper triangular block matrices in sign pattern matrices with the form of frobenius,providing the method to construct the idempotence in sign pattern matrices,researching the relations between the sign idempotent and the allowance of idempotent.

sign pattern matrix；sign idempotent；allowance of idempotent

O157.5

A

1673-1980(2012)05-0172-04

2012-04-09

云南省自然科学基金项目(2006A0089M)；云南省教育厅科研基金项目(2007C112006)；大理学院青年教师科研基金项目(KYQN2010-18)

朱兴文（1985-），男，云南宣威人，硕士，助教，研究方向为组合数学与组合矩阵论。