自平衡电动车控制系统建模与低成本传感器应用仿真
田珊珊 杨志刚 贾 伟
(重庆交通大学,重庆 400074)
自平衡电动车控制系统建模与低成本传感器应用仿真
田珊珊 杨志刚 贾 伟
(重庆交通大学,重庆 400074)
应用动力学原理和拉格朗日方程对自平衡电动车建立系统的动力学数学模型。在Matlab/Simulink环境下,采用PID控制器与自平衡电动车动力学模型构成闭环控制系统,对控制信号加入低成本传感器造成的系统误差进行数字仿真,仿真结果表明了所建模型和PID控制方法的可行性。
自平衡技术;动力学分析;PID控制;误差分析
自平衡电动车是一种平行两轮左右布置的单人电动车。自从美国segway公司发明并生产了这种自平衡电动车后,日本等国也进行了大量的技术开发工作。近年来我国一些高校和企业也进行了产品开发,并进行了小批量生产。由于自平衡电动车的前进、后退、转弯、速度快慢以及车体的平衡等控制均由两个驱动电机承担,所以控制难度较大。因而,需要动态性能较好的传感器检测它的实时姿态,而陀螺仪传感器和倾角传感器等高精度、反应快的传感器价格昂贵且占整车总成本的比例较大,在国内推广应用受到制约,所以如何改用低成本的传感器以降低产品价格,并且如何选用适当的控制算法以满足车辆运行的实时控制要求,是本文研究的重点。
1 车体系统建模
车体总体图见图1。建立一个固连在车体的动坐标系X-Y-Z和固联于地的静坐标系X′-Y′-Z′,以车体行走方向为Y轴,车轮轴线为X轴,铅垂线为Z轴,车体和人体的质心为P点,建立系统物理模型如图2所示。
由图可以看出,车体运动具有3个自由度,分别是绕X轴的旋转运动,用俯仰角θP和俯仰角速度ω来反映其绕X轴旋转运动状态;质心沿Y轴方向的位移YRM和移动速度VRM;绕Z轴的横摆角δ和横摆角速度δ˙。由以上6个状态变量构建的状态方程完全描述该三自由度系统的动态特性。由于车体没有差速机构,它的转弯运动是通过左右电机的转速差来调节的,所以系统的输入量为左右轮的输入电压UL和 UR,输出量为YRM、VRM、θP、ω、δ、δ˙。利用Lagrange方法建立系统的动力学方程。系统动能包括:左右车轮的平动动能,左右车轮绕x轴的转动动能,车体和人体的总动能可分解为两者随车轴的平动动能和两者绕车轴水平轴线的转动动能,以及车体绕垂直方向轴Z的转动动能。系统的总动能:
图1 车体总体图
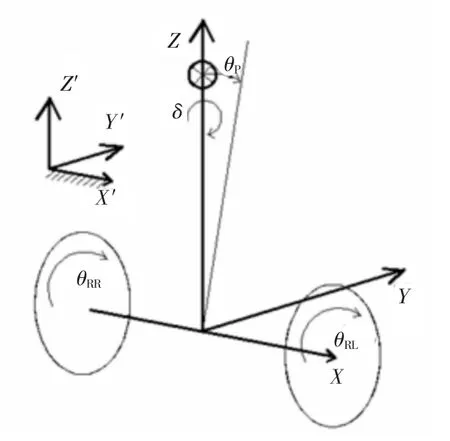
图2 车体系统的坐标图

式中:MRL、MRR—左右车轮质量;YRL、YRR—左右车轮位移;JRL、JRR—左右车轮转动惯量;θRL、θRR—左右车轮转角;Mp—车体和人体的总质量(不包括车轮质量);L—车轴与质心P的距离;YRM—质心的位移;JP—车体绕质心水平轴的转动惯量,Jδ—车体绕Z轴的转动惯量。
在完整约束的条件下,确定质点位置的独立参数的数目等于系统的自由度,显然小车在平面运动时具有三个自由度。选取质心的位移q1=YRM,摆杆绕X轴的俯仰角q2=θP,摆杆绕Z轴的横摆角q2=δ作为系统的运动状态变量。显然用(YRM,θP,δ)来描述系统具有完整约束,可以惟一决定质点的位置而且它们是相对独立的。因此选用YRM,θP,δ作为系统的3个广义坐标,在此坐标体系下,相应的广义力为:
电机对左右车轮的作用转矩: Q1=TdL+TdR
车体重力与电机对车体作用的转矩

电机对车体转弯作用的转矩: Q3=TdL-TdR
用广义坐标表示的拉格朗日方程为[2]:

由于选用同一型号的电机,因此可以认为具有相同的力矩系数km和反电动势系数ke,设电机内阻为Rs,电机的电磁转矩为Tm,电机的输出转矩为Td,齿轮传动比为i,齿轮传动的机械效率为η,加在左右轮上的电压分别为UL和UR,故有:

将系统总动能广义坐标、广义力矩、车轮转矩代入拉格朗日方程,经过计算和简化,可得到系统的运动方程:


并用矩阵形式表示如下:
式(8)可简单表示为:A2x˙A1x+B1u,则另自平衡两轮电动车的状态空间模型为

状态方程式(8)中的参数如下:
反电动势常数 ke=0.187 3V·s·rad-1;
转矩常数km=0.198 0N·m/A;
车体和驾驶者的质量Mp=114.844kg;
183cm的驾驶者的质心高度为801.087 5mm;
摆杆回转轴到总体质心的距离L=647.659mm;
摆杆前后摆动的转动惯量Jp=65.153 8kg·m2;
摆杆左右摆动的转动惯量 Jδ=1.569kg·m2;
车轮的转动惯量Jr=0.043kg·m2;
轮的质量MR=5.4kg;
车轮间的距离D=0.52m;
轮的半径R=0.2m;
减速机构的传动比i=5.230 8;
减速机构的传动效率η=98%。
通过观察系统状态方程,可以发现车体做转弯运动和直线运动时,车体的状态参数δ,δ˙与状态YRM,VRM,θP,ωP之间是互不相关的,所以可以将控制系统分解成两个独立的控制子系统。
为了降低车体的成本,选用低成本陀螺仪和倾角传感器。然而,低成本陀螺仪和倾角传感器在采集车体姿态信息时,比高价位的传感器采集信号的精度差。本文主要考虑传感器造成的系统误差对状态方程和输出响应的影响。把俯仰角传感器精度差引起的系统误差ΔθP视为干扰信号引起的变化,ΔθP=0.013rad,表现在状态方程中为:

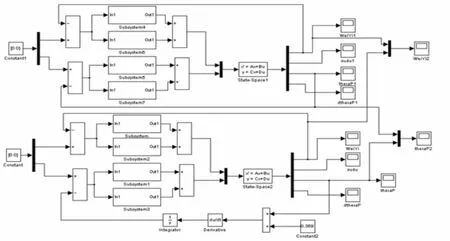
图3 PID控制系统
其中,令系统误差 d=(0 0 0.396 0)T。
2 车辆PID控制系统仿真
系统在控制过程中存在误差,所以,为保证系统的准确稳定,选择能够消除误差的控制方法。首先,采用闭环控制负反馈系统以提高系统抑制干扰信号的能力;其次,在控制算法上选用能够消除干扰信号的算法,如前馈反馈控制、状态观测器等;由于系统误差为常数,经过微分电路处理就能把系统误差去除,再经积分电路就可得到理想的俯仰角度。
在Matlab环境下进行仿真研究以便设计并整定控制器的参数。为了实现控制目标,必须不断增大比例环节的值,但系统的超调量也随之增大,且系统趋于不稳定,此时需要微分环节进行预测误差变化趋势,遏制输出的上升势头,避免严重的超调,并且使系统的调节时间减少。最终完成3个PID控制器参数的整定,Kp=-200,Kd=-13.5,Ki=0.1,可以得到较好的控制曲线。在Matlab/Simulink中搭建PID模型,如图3所示。
车体可控偏移角度不是随电机扭矩提高而一直增大的,它存在极限值,这个极限角度值是受车体运行环境路面的摩擦系数限制的[1]。在实际环境中,设定本车体摆杆的最大俯仰角为15°。
为了证明PID控制的有效性,在PID参数相同的情况下,对加入摆杆俯仰角度系统误差的状态方程与理想的(这里可认为是高价格的传感器)摆杆俯仰角度的状态方程的输出位移和俯仰角曲线进行仿真比较。观察两条曲线的差异,比较是否PID具有较强的抗干扰性能。将倾角传感器测量的值与加入倾角传感器系统误差的值代入PID控制系统进行比较,得到的仿真图像见图4。

图4 俯仰角θp仿真曲线和局部放大图
将加入倾角传感器系统误差的控制系统与理想控制系统比较,输出俯仰角的两条曲线几乎重合,在俯仰角度曲线的局部放大图中可以看出两条曲线稍微有点差异。所以,使用低成本姿态传感器测量数据信号的系统在经过信号处理之后,输入到PID控制器并对系统位移和俯仰角度进行控制,可达到良好的控制效果。摆杆在偏离垂直位置15°时,系统可在3s内恢复平衡。
3 结 语
低成本传感器低其线性度较差,检测车体的实时姿态信息存在较大的误差。而本文设计的PID控制器对建立的3自由度系统进行控制时,控制效果良好,从而避免因传感器造成的误差。说明本文PID控制器的设计是切实可行的,可以应用在实时性要求较高的场合。
[1]程刚,屈胜利,刘学超,等.两轮自平衡小车可控角度的推导研究[J].机床与液压,2009,5(37):115-117.
[2]张培仁,杨兴明.机器人系统设计与算法[J].理论分析和数学模型建立,2008(10):156-160.
Control System Model of Self-balancing Electric Vehicle and Low-cost Sensor Application Simulation
TIAN Shanshan YANG Zhigang JIA Wei
(Chongqing Jiaotong University,Chongqing 400074)
By using dynamics mechanics theory and the equation of Lagrange,the Self-balancing Electric Vehicle,and establishment of the dynamics mathematical model of the system is made.In Matlab/Simulink,the PID controller and the dynamics model are composite of closed loop control system.It is simulated the control signal which is add the system error of low cost sensor in digital.In the end,the simulation result proves the responsibility of the model and the control of PID.Through the experiments verified that the rationality of the system modeling and the designed fuzzy controller.
the technology of self-balancing;dynamics analysis;PID control;error analysis
TP13
A
1673-1980(2012)05-0158-04
2012-05-15
国家自然科学基金项目(51008321)
田珊珊(1986-),女,山东人,重庆交通大学在读硕士研究生,研究方向为汽车电子及控制。

