应用信息粒方法构建测井岩性解释模型

余翔宇，徐义贤，骆 淼

（中国地质大学 地球物理与空间信息学院，湖北 武汉 430074）

0 前言

作为地球物理测井的重要工作之一，根据岩心取样分析资料和对应的测井数据来构建岩性解释模型，进而由测井曲线来进行岩性识别已成为许多地质工作的基础［1］。而岩性解释（识别）模型的实质，就是一个运用各种多元统计分析方法所建立的岩性样品，与其对应测井物性参数向量之间的回归模型［2］。由于地球物理资料解释本身的多解性，测井参数向量（自然伽玛、自然电位、电阻率、声波、中子、密度等）与岩性之间的关系表现出不确定、模糊、高度非线性的特点［3］。传统意义上定量求取参数建立测井响应方程的方法计算复杂，解释效果也并不理想［4］。现今的研究者们则更多地应用人工智能领域里的方法与技术，如模式识别、模糊数学、人工神经网络等，来建立各种岩性解释模型，，并取得了良好的效果［5］。

作为人工智能中拟合非线性回归模型的最主要方法，人工神经网络不明确定义出回归方程的形式，而将回归方程的结构与参数隐藏于网络的各个神经元节点以及节点之间的连接关系中；然后通过不断的学习和训练来调整各个神经元节点间的连接权值，使得输入与输出之间的误差最小［6］。人工神经网络的定义（包括网络类型、隐层数、神经元节点数、激活函数等）非常灵活，在岩性识别应用中可选择的神经网络类型也很多。虽然训练数据的自身特点（如数据量的大小、数据的分布等）会直接影响到神经网络的选择，但并没有严格的数学证明应用哪种结构的神经网络会取得最好的结果。

而作为模式识别中的重要方法之一，聚类分析同样在岩性解释模型的构建中得到了广泛的应用。

普通聚类方法（HCM）从训练数据自身的特点出发，由样本点之间的距离远近来对样本空间进行划分，并形成若干个聚类。比较测井数据到各个聚类中心点的距离，就能确定它属于哪个聚类，即判定该数据具有与该聚类中心点相同的岩性特征。

而模糊聚类（FCM）则认为数据并不严格属于某一个聚类，它以数据与各个聚类中心点的接近程度来量化其属于该聚类的模糊隶属度，再由模糊隶属度与其聚类中心点的综合计算来确定其岩性划分。

相对于普通聚类、模糊聚类在岩性识别应用中通常能取得更好的效果［7］。但无论哪种聚类方法，其更多的是从数据自身的特点出发，并在无监督的状态下进行，而应用中每个聚类的大小并不一样。因此，它常常无法根据数据与知识的真实匹配关系，来对聚类中心点进行灵活的调整。

作为模糊数学与神经网络的结合体，模糊神经网络也在岩性解释模型的构建中得到了良好的应用［8］。从理论上来讲，模糊神经网络能将模糊推理应用于神经网络之上，将两者的优点进行有效的结合。但由于模糊系统和神经网络都各自种类繁多，构建怎样的模糊神经网络能在实际应用中取得较好的效果成为了一个重要问题。作者在本文将要描述的就是一种能够将模糊聚类与径向基神经网络（RBFNN）进行有效结合的方法，及其如何应用该方法于测井岩性解释模型的构建中。

1 信息粒解释模型

信息粒（Information Granulation）是在模拟人类对于信息的表示和使用时所产生的一个概念，它将人们对数据的关注从点的层面提升到集合的层面［9］。站在信息粒的角度看，人们之所以在日常生活中将许多数据作为一个集合来使用，是因为该集合中包含了一个或若干个信息粒，这些信息粒既可以显式表达为确定性的逻辑知识，也可以将非确定性的知识（模糊判定）蕴涵其中。特别对于后者，信息粒可囊括所有与聚类相关的类型，如普通聚类、粗糙集、阴影集、超盒等。从模糊数学的角度来看，任何数据都必然会与某些信息粒存在着模糊隶属关系，而信息粒解释模型的实质就是利用数据与信息粒之间的模糊隶属关系，在神经网络上进行推理计算，从而建立起不同数据之间的映射［10］。

信息粒解释模型框架可表述如图1所示，其中输入层和输出层与普通神经网络一致，中间层则由信息粒产生与信息粒解释两个部份组成。

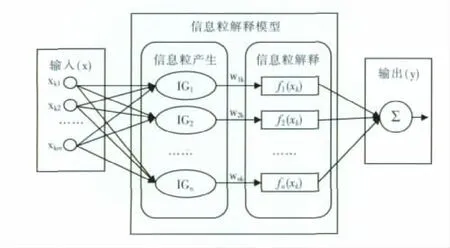
图1 信息粒解释模型框架Fig.1 Architecture of IG interpretation model

输入数据在信息粒产生部份被划分到若干个信息粒集合（以模糊聚类为例）里，每一个模糊聚类所表达的信息粒中都蕴含着至少一种既定的模糊判定，可简单的用if…and…then来描述。由图1可知，模糊聚类的个数与最后输出的输出结果数并不是一致的，最后的输出结果是由这些信息粒（模糊聚类）的加权综合决定（见式（1））。而式（1）中影响最终输出的权值则由数据从属于各个模糊聚类的模糊隶属度来衡量，即wik表示的是数据xk对聚类i的模糊隶属度。

信息粒解释部份则利用某种既定的函数形式，来对每个信息粒所对应的模糊判定进行描述。从理论上讲，函数形式的定义较自由，但在实际应用中以多项式函数居多。如对于模糊聚类产生的信息粒，可定义出式（2）～式（5）四种与聚类中心相关的解释函数形式。

（1）常数类型函数：

（3）二阶多项式函数：

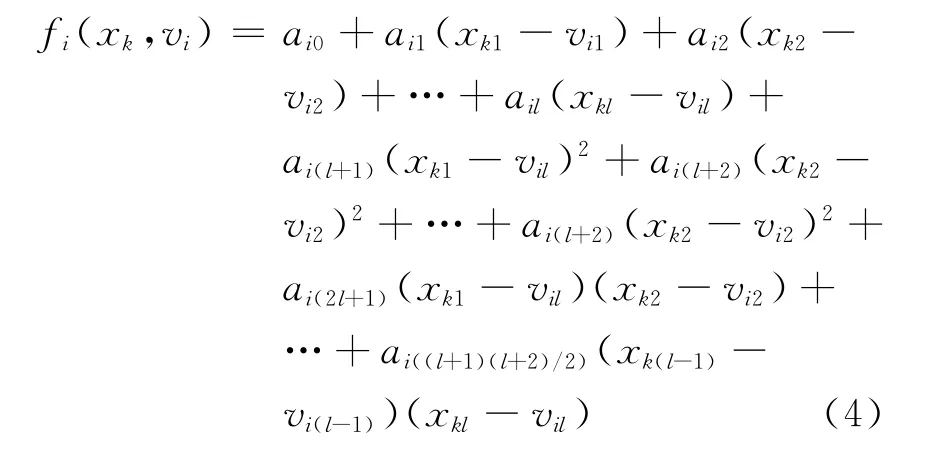
（4）变形二阶多项式函数：

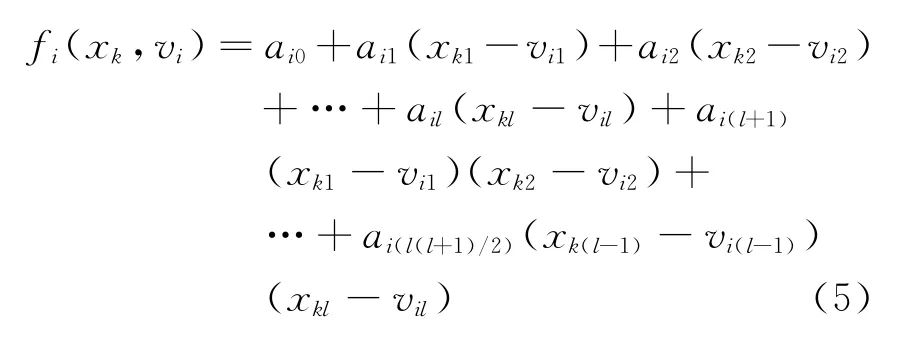
式中 xk＝ ｛xi1，xi2，…，xil｝为输入向量，vi＝｛vi1，vi2，…，vil｝代表第i个聚类中心［11］。

通过使粒模型解释函数的计算结果与训练数据的映射误差最小，就可以确定这些粒模型解释函数的参数。假设粒模型解释函数结构取式（3），则问题实质上就转化为如何对多项式系数ai＝ ［ai0ai1…ail］进行优化，使目标函数式（6）取得最小值。

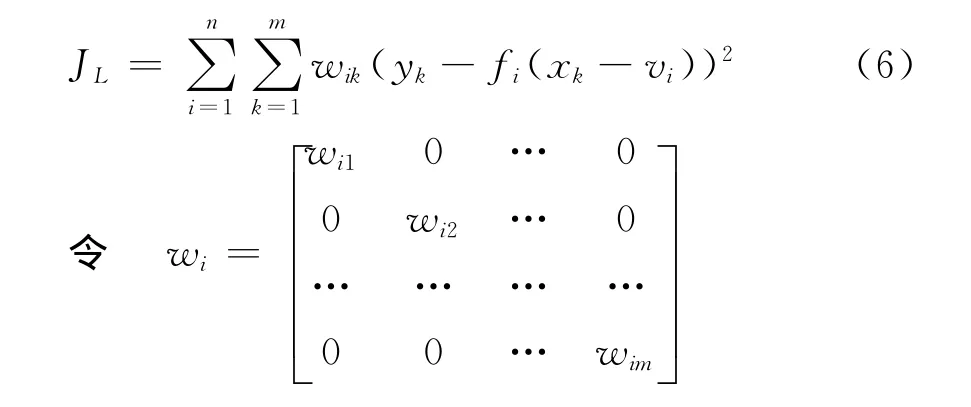
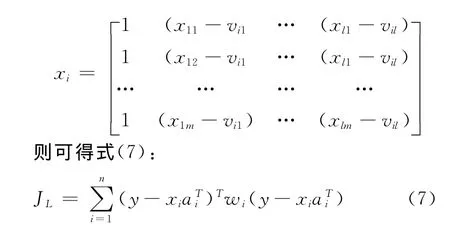
利用加权最小二乘（WLS），可求得JL取最小时ai的值，表示为式（8）。

在实际应用中，粒模型解释函数的形式确定，以及聚类个数的选取，也可通过使用智能优化算法（如遗传等）来达到比较理想的效果［12］。

2 模型应用

作者以CCSD测井数据的岩性识别为例，详细介绍了信息粒方法在构建岩性解释模型中的应用。作者取100m～1 948m的451个测井数据与其对应的岩性取样结果作为训练数据，然后再以建立的模型来对从CCSD测井数据中任意抽取的150个向量进行验算，最后将模型得到的计算结果与取样资料进行比较来验证其准确率。其中，定义输入向量x由12个元组组成（深度、井径、自然伽玛、深电阻率、密度、声波时差等），输出y为量化好的岩性值，如表1所示。

在表中y的取值共对应了十二种岩性（包括正片麻岩、角闪岩、绿泥石角闪岩、蛇纹岩、片岩等），分别用数值1～12来进行量化。

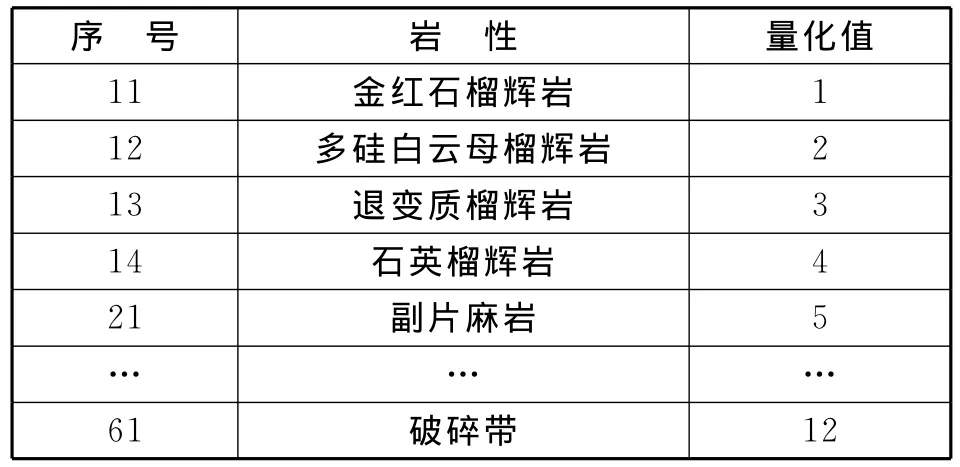
表1 输出量化值Tab.1 Output value

确定好输入输出后，作者根据训练数据量的大小，来确定所使用的信息粒解释函数类型。由于模型所输出的岩性种类为12，所以大致可确定模糊聚类的个数不应小于12（k≥12），而输入数据的向量维数为12（n＝12）。对应于以式（2）～ 式（5）四种信息粒解释函数，可知其待定参数个数（即a矩阵元素）分别为k个、（n＋1）＊k个、（n2＋3n＋4）＊k／2个、（n2＋n＋2）＊k／2个。由于参与模型构建的训练数据向量个数为451，显然如采用式（4）和式（5）的信息粒解释函数，则待定参数个数会大于方程个数，无法得到有效解。比较函数形式（2）和式（3）可知，在聚类数适中的情况下式（3）的解比较有效；在聚类数较大的情况下，则只能选择式（2）。但同时聚类数的增大意味着更多的迭代次数，计算量也相应增加。

经过上述分析，作者所最终选用的信息粒解释函数为式（3），信息粒（聚类）个数k则选在15～24之间，并根据计算结果来选择一个最优解（最终选定的k值为18）。整个计算步骤如下：

（1）对训练数据进行模糊聚类，确定k个聚类中心点，以及每个训练数据向量分别对应于k个聚类中心点的模糊隶属度［13］。

（2）利用式（8），根据实际岩性输出y值，求解出信息粒解释函数的参数矩阵a。

（3）将用于验算的测井数据来分别计算其到k个模糊聚类中心的距离，并求解其到这k个聚类的模糊隶属度。

（4）由建立好的信息粒解释函数来求解输出的岩性量化值（四舍五入），根据该量化值与岩性的对应关系，得到最终的岩性解释输出。

最终应用构建好的岩性解释模型所得部份，计算结果见下页图2。

将解释模型计算结果与岩芯取样资料进行对比分析，总体来看，计算正确率达到了85.6%。在岩性识别有误的数据中，模型计算所得的岩性量化值，总是大于实际取样的岩性量化值，且其偏差值最多为“3”。如在1 130m～1 137.4m段，计算岩性量化值为“9”，代表其岩性为绿泥石角闪岩；而实际取样资料的岩性为正片麻岩，对应的岩性量化值为“6”。另外与所有聚类方法一样，聚类中心的精确程度对最后计算结果的准确度，有着决定性的影响。由下页图2可知，CCSD实验数据中RD（深电阻率）分量数值变化范围最宽（1 330～95 500），DEN（密度）分量变化范围最窄（1～5），这就决定了聚类中心对各个分量值变化敏感程度的不一致。试验表明，当RD分量的变化较小而DEN分量变化较大时，模型计算的岩性结果较容易出错。

3 结论

由实际应用效果可知，基于信息粒技术构建的解释模型，能够得到准确性较高的岩性解释结果。该方法的实质就是利用数据本身的特点将其划分成集合，然后对这些集合的特征进行解释，从而建立起信息粒与知识的映射过程。它具有以下特点：

（1）信息粒模型在构建过程中将模糊聚类与神经网络的特点进行结合，模型的结构既遵循一定的框架规范，又可以在实际应用中进行有效的优化调整［14］。

（2）模型可由数据的特点来选择不同的信息粒解释函数，将数据的回归特征蕴含于解释函数的参数中。特别适用于训练数据丰富，训练数据维数较高的解释模型构造［15］。

（3）模型建立过程中的计算量相对较大，无论是模糊聚类还是加权最小二乘的应用，都以较大的计算量为代价。在实际应用中，可采用并行计算方法提高信息粒解释函数参数矩阵求解的效率［16］。

（4）在训练数据较多的实际应用中，可选择智能计算方法（如遗传算法、粒子群算法等）来对模型进行结构优化，选择最合适的信息粒个数和解释函数形式，进一步提高准确率［17］。

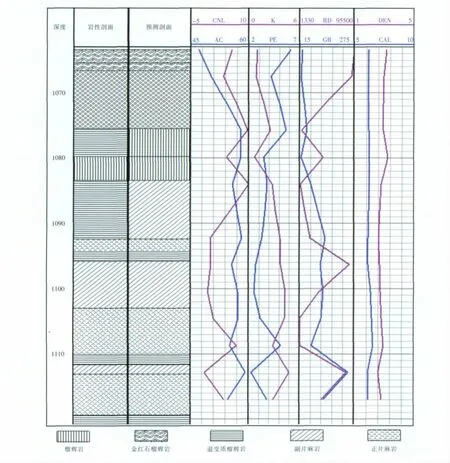
图2 解释结果Fig.2 Lithology interpretation

［1］廖太平，张福荣，张志坚.基于模糊聚类算法的复杂岩性识别［J］.大庆石油学院学报，2004（12），28（6）：58.

［2］刘秀娟，陈超，曾冲，等.利用测井数据进行岩性识别的多元统计方法［J］.地质科技情报，2007，31（9）：109.

［3］牛林林，刘颖卓，刘平安.基于一种改进的模糊神经网络方法识别岩性［J］.国外测井技术，2005，20（5）：56.

［4］李继安.人工智能神经网络在岩性识别、孔隙度和渗透率预测中的应用——以十红滩铀矿床为例［J］.西北地质，2010，43（2）：32.

［5］汪宏年，李舟波，杨善德，等.复杂岩性解释模型稳定性和可靠性评价［J］.地球物理学报，1998，41（4）：561.

［6］张平，潘保芝，张莹，等.自组织神经网络在火成岩岩性识别中的应用［J］.石油物探，2009，48（1）：53.

［7］徐海波，李瑞，邹炜，等.模糊聚类实现岩性自动划分［J］.物探化探计算技术，2006，28（4）：319.

［8］热合木江，古丽·吐尔逊，艾尼瓦尔·买买提，等.应用模糊神经网络识别岩性［J］.广西师范大学学报：自然科学版，2003，21（1）：58.

［9］Y.Y.YAO.Information Granulation and Rough Set Approximation［J］.International Journal of Intelligent Systems，2001，16（1）：87.

［10］WOOK DONG KIM，SUNG KWUN OH，WEI HUANG.Optimized FCM－Based Radial Basis Function Neural Networks：A Comparative Analysis of LSE and WLSE Method［J］.Lecture Notes inComputer Science.2010，60（63）：207.

［11］WEI HUANG，LIXIN DING.Identification of Fuzzy Inference System Based on Information Granulation［J］.KSII Transactions on Internet And Information Systems.2010，84（4）：575.

［12］JEOUNG NAE CHOI，YOUNG Il LEE，SUNG KWUN OH.Fuzzy Radial Basis Function Neural Networks with Information Granulation and Its Genetic Optimization［J］.Advances in Neural Networks－ISNN 2009（5552）：127.

［13］BEZDEK JC.Pattern Recognition with Fuzzy Objective Function Algorithms［M］.New York：Plenum Press，1981.

［14］NATARAJA M C，JAYARAM M A，RAVIKUMAR C N，Prediction of Early Strength of Concrete：A Fuzzy Inference System Model［J］.International Journal of Physical Sciences.2006（1）：47.

［15］GRANATH G.Pattern recognition in geochemical hydro－carbon exploration：A fuzzy App roach［C］.Emerging MGUS，1988.

［16］STAIANO A，TAGLIAFERRI R，PEDRYCZ W.：Improving RBF Networks Performance in RegressionTasks by Means of a Supervised Fuzzy Clustering［J］.Neurocomputing，2006（69）：1570.

［17］GAING Z L，A particle swarm optimization approach for optimum design of PID controller in AVR system［J］.IEEE Trans.Energy Conversion.2004（19）：384.