卵形线坐标计算方法研究

中铁十三局集团 第四工程有限公司 刘基强

卵形线坐标计算方法研究

中铁十三局集团 第四工程有限公司 刘基强

卵形线是公路测设中的一种复杂线形。其坐标计算在理论上没有给出准确的计算公式，工程中常用的计算程序也大多采用简化的计算公式，当曲率半径较小时误差较大，其偏差可达数厘米，这对于高等级的公路和建筑物、构造物而言，是不可接受的。本文，笔者经过严密推导，给出了利用虚起点进行卵形线坐标计算的精确公式，并用Casiofx4800程序予以实现。

一、卵形线坐标计算原理

1.虚起点的计算。卵形线是由左边为半径为R1的圆曲线，右边为半径为R2的圆曲线通过一段回旋线连接构成的曲线。假设R1＞R2，由回旋线的特征可知，将回旋线向左延伸到曲率半径无穷大的虚起点处，此点在坐标计算时相当于一个直缓点，只要计算出该点的坐标、里程及切线方位角，那么整个卵形线的计算即与基本形一致，然后按基本形的计算即可。

设YH点的里程为K1，切线方位角为C1，坐标为X1，Y1；HY点的里程为K2，切线方位角为C2，坐标为X2，Y2；回旋线长为L2；虚起点的里程为K0，切线方位角为C0，坐标为X0，Y0；YH点到虚起点的长度为L1，HY点到虚起点的长度LS=L1+L2。假设曲线右转，且K1＜K2，C1＜C2，则HY点和YH点的转角为Δβ=C2-C1，由回旋线特征有

则虚起点的里程K0=K2-LS，切向方位角为C0=C2-LS/2R2。

令T=R2Ls，则HY点在虚起点处切线方向为X轴、法线方向为Y轴的坐标U，V分别为：

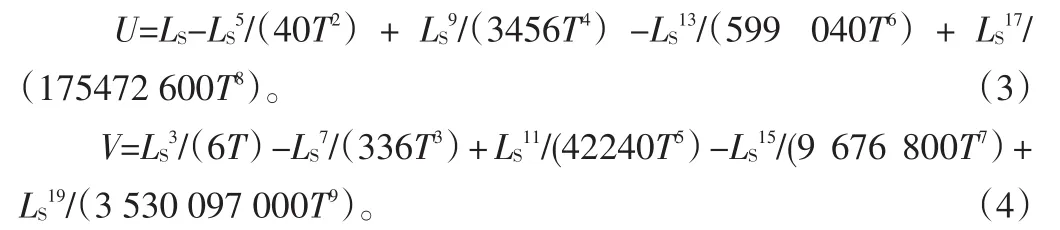
则HY点到虚起点的弦长为：

弦线方位角为：

故虚起点的坐标为：

若R1＜R2或C1＞C2或K1＞K2，则只需将上述公式做适当改动即可，其计算原理和步骤基本一致。

2.回旋线上任意一点坐标的计算。设回旋线上任意一点P的里程为K，则P点到虚起点的长度L=K-K0，用L代替式公式（3）和（4）中的Ls，则可得P点在虚起点处切线方向为X轴、法线方向为Y轴的坐标UP，VP，再根据式（5）得虚起点至P点的弦长SP，弦线方位角θP=C0+Tan-1（VP/UP），故P点的坐标为：

其切线方位角为

设P点左边桩距中桩的距离为SL，右边桩距中桩的距离为SR，中桩与左边桩连线的坐标方位角为CL=Cp-/2，中桩与左边桩连线的坐标方位角为CR=Cp+/2，则左边桩的坐标为：

同理，右边桩坐标为：

三、程序实现

程序代码如下∶

程序中Δ为判断中止符，在Casiofx4800中为◢，行号和行号后面的冒号只起分行作用，不用输入。

四、结论

本文，笔者根据结合工程实际的需要，分析、推导了卵形线坐标的计算，给出了一种计算卵形线坐标的新方法。该计算方法具有以下优点：

1.采用虚起点的计算方法，整个计算过程理论严密，逻辑性强。

2.坐标计算级数展开的阶数较高，从而保证了计算的精确度。

3.整个计算过程可以利用Casiofx4800编写成易于操作的程序，方便了工程建设人员及相关人员的使用，具有推广价值。