改进PSO训练的BPNN方法的舰船主尺度建模

张海鹏，韩端锋，郭春雨

(哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001)

航母作为一种高科技含量的战斗舰艇，其排水量与船体要素之间存在紧密的客观联系，二者的统计回归与数学建模研究较少，因此在航母顶层设计阶段如何根据目标图像要求确定航母总体要素成为亟待解决的问题.

船舶总体设计包括主尺度要素确定、型线设计、总布置以及结构设计等多方面内容，其中主尺度要素的确定是各项工作的先决条件.寻求有效方法将船舶总体要素建立成数学模型可作为顶层概念设计与合同设计的参考准则与设计依据，具有不可替代的重要意义［1］.

目前广泛采用基于数理统计理论的回归方法来建立数学模型，如多元线性回归分析和逐步回归分析方法等［2］.近年来，随着人工智能理论的发展，计算机神经网络技术得到越来越多的关注与运用［3］.本文首先介绍传统多项式回归分析方法与基于学习因子自适应调整的改进粒子群优化算法(particle swarm optimization，PSO)，并将改进后的PSO算法嵌入到BP神经网络中，实现对BP神经网络训练过程的优化.其次利用经改进粒子群优化后的BPNN对国外航母主尺度数据资料建立数学模型，并将其与基于传统多项式回归分析方法的结果进行对比分析.

1 回归分析与神经网络优化

1.1 多项式回归分析

若回归方程表达式为

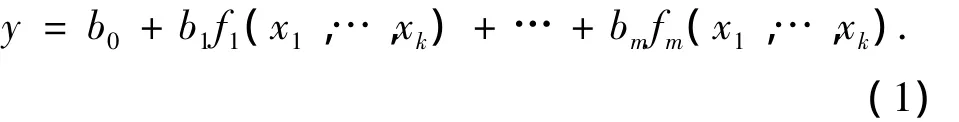
式中:fi(x1，…，xk)都是自变量的已知函数，且不包括任何参数.令:

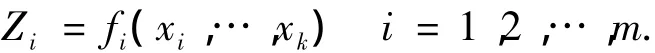
则上述方程可表示为

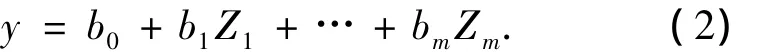
因为对于任意连续函数上的一点，总可以在其邻域内用多项式来逼近它，所以对于较复杂的问题，可用多项式回归进行分析计算.

1.2 改进的粒子群算法

PSO最早由Eberhart等在1995提出［4］，通过模仿鸟类群体行为进行最优值搜索.

设在n维的搜索空间中，由m个粒子组成的种群记为X=［x1… xi… xm］.其中，第i个粒子的位置为xi=［xi1xi2… xin］T，其速度为vi=［vi1vi2… vin］T.粒子i的个体位置为pi=［pi1pi2… pin］T.粒子在搜索过程中通过跟踪2个目标值来更新自己的速度和位置:1)粒子本身目前找到的最优解，即个体极值;2)整个种群目前找到的最优解，即群体极值.其迭代计算公式为

在粒子群优化算法中，学习因子c1、c2分别控制“认知”部分和“社会”部分对粒子速度的影响.一般来说，在基于种群的优化方法中，总是希望个体在初始阶段能够在整个寻优空间进行搜索，不至于过早陷入局部值;而在结束阶段能够提高算法收敛速度和精度，有效地寻找到全局最优解［5-7］.本文提出一种加速系数随迭代进程基于“S”型函数动态变化的调整方法:

式中:a为正系数，控制c1的下降陡峭程度，建议取在5～15;kmax为最大迭代次数，k为当前迭代次数.该方法可最大程度使粒子群在迭代初始阶段具有大的“认知”部分，而在迭代后期阶段具有大的“社会”部分，这样更有利于算法收敛于全局最优解，提高算法收敛速度和精度.改进后的c1、c2函数曲线如图1所示.

图1 改进后的学习因子c1、c2Fig.1 Improved learning factors c1，c2

1.3 经改进PSO优化的BP神经网络

BPNN是一种多层结构的前向网络［8］，其神经网络结构模型如图2所示.

图2 BP神经网络层次结构Fig.2 Layers of BP network

其隐层神经元的激活函数为S型函数，而输出神经元的激活函数可以是S型函数，也可以是线性函数.它可以实现从输入到输出的任意非线性映射.典型的S型Sigmoid函数如下:

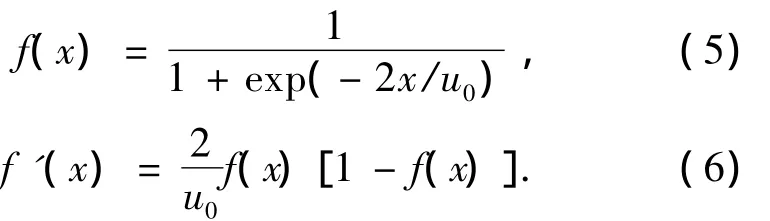
由于传统BP算法是基于梯度下降这一思想的，因此不可避免地带来以下问题［9-10］:

1)从数学上看，它是一个非线性优化问题，这就不可避免地存在局部极小问题;

2)运算量大，训练时间长，收敛速度慢;

3)鲁棒性差，网络对参数的初始设置比较敏感;

4)网络的结构参数和运算参数等都尚无公认的理论指导，往往是根据经验选取的，一旦选择不当系统性能将恶化，甚至导致不收敛.

改进PSO算法避免了梯度下降法中要求函数可微、对函数求导的过程，因此用PSO算法替代BP算法中的梯度下降法训练神经网络的参数，能够改善BPNN性能，加快搜索速度，并且能够防止整个算法的过早收敛，使其不易陷入局部极小，增强了网络的泛化性能.

在BPNN学习中，用改进的PSO算法替代传统BP算法，粒子群结点由位置向量和速度向量表示.其中，位置向量用BP网络的权值和阈值而定义，即假设BP网络为三层结构，令R、S1、S2分别为输入层、隐层和输出层神经元的个数，则粒子群个体位置向量x的维数n为BP网络的权值和阈值个数之和，即

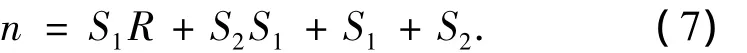
在粒子群节点速度向量的定义中，每一维粒子都有一个最大限速度vmax(vmax＞0)，如果某一维的速度超过设定的vmax，则该维速度被限定为vmax.

粒子群结点适应度函数使用BP算法的均方差MSE(mean squared error)定义:

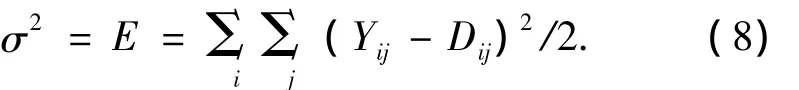
式中:Yij是节点的期望输出，Dij是节点的实际输出.

图3 PSO-BP网络算法流程Fig.3 Flow chart of PSO-BP

可见，对于给定的神经网络结构，只需对连接权值进行编码，将其映射为码串所表示的个体，同时将训练中产生的均方误差作为评价个体的适应函数，此时神经网络的训练就可转化为寻找一组使均方误差最小的最佳连接权值的优化问题.基于改进PSO的BPNN算法流程图如图3所示.

2 主尺度回归模型建立

通过搜集、筛选近50年现役及退役的国外航母主尺度资料，选择了其中具有代表性的15艘［11］，将其主尺度分别利用上述多项式回归与改进PSO-BP神经网络建立数学模型.通过这些数学模型不仅可以反映出近现代航母发展的基本走势，还可为在航母顶层论证与初步设计阶段提供一个预报与评价主尺度与船型系数的科学依据，并通过对回归公式进一步的理论研究总结出某些回归变量间的内在理论联系，为科研与设计单位提供较为全面、系统的参考信息.

考虑到航母设计之初主要以满载排水量为目标图像［12］，故以满载排水量 Δ =LBTCBρ作为输入，分别以船总长L、总宽B、设计水线长Lw、设计水线宽Bw和吃水T作为输出.分别采用基于多项式回归的Matlab Curve-fitting tool工具箱与基于BP神经网络算法的Matlab BP工具箱中的网络设计函数与网络仿真函数［13-14］，建立了国外典型航母主尺度的数学模型.采用多项式回归的船舶主尺度与满载排水量的回归关系式为

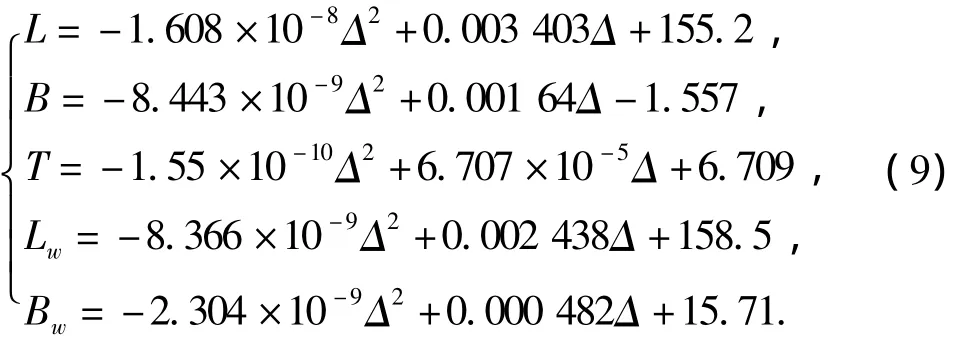
船总长L、总宽B、吃水T、设计水线长Lw与设计水线宽Bw的拟合结果分别如图4～8所示.

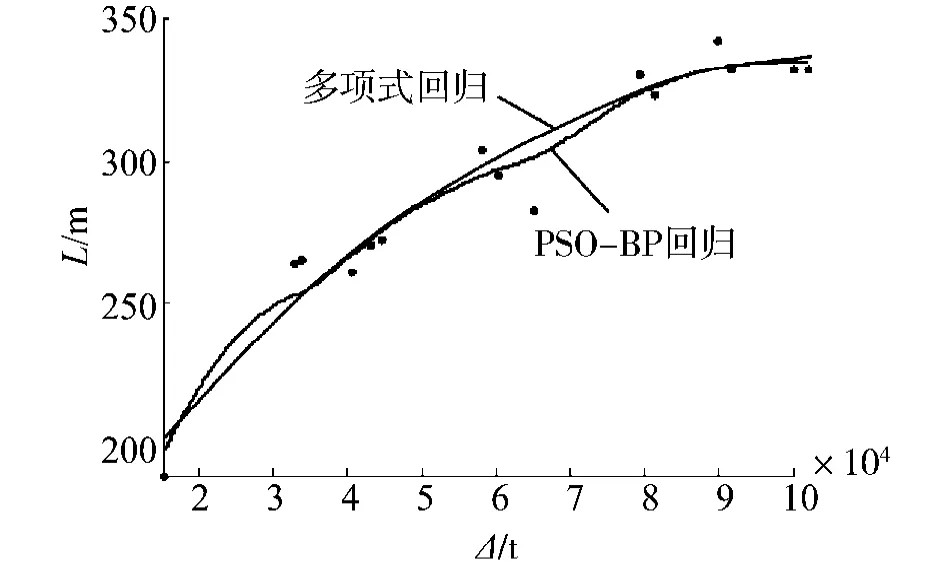
图4 总长L与满载排水量Δ的多项式与PSO-BP回归Fig.4 Polynomial and PSO-BP regression of L and Δ

表1 给出了其中吃水T与设计水线宽Bw的计算结果，从中可以看出采用改进PSO-BP方法进行回归的结果比较准确，与实际值比较接近.

表1 15艘典型航母吃水与设计水线宽以及2种方法的回归值Table 1 15 AC＇s draft and breadth of waterline and the regression value

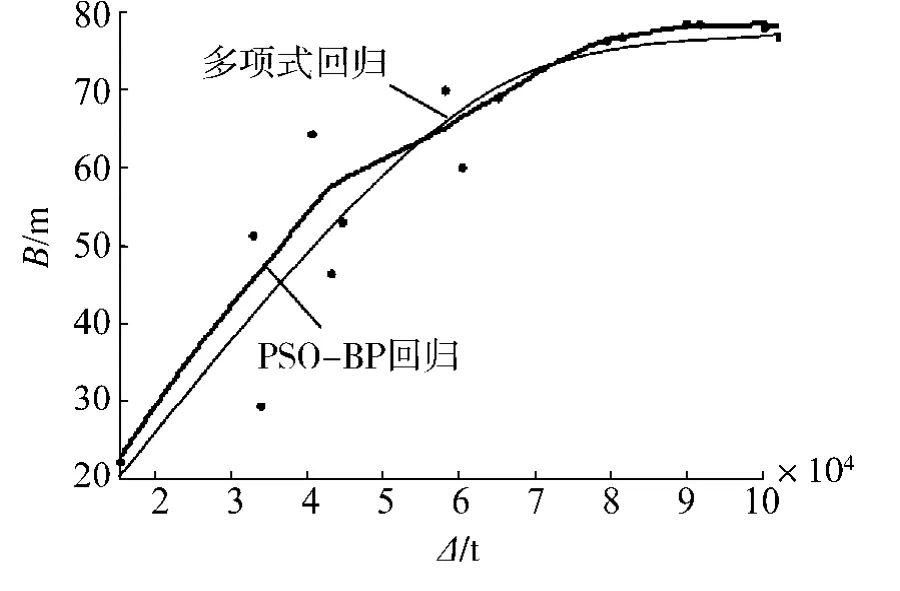
图5 总宽B与满载排水量Δ的多项式与PSO-BP回归Fig.5 Polynomial and PSO-BP regression of B and Δ

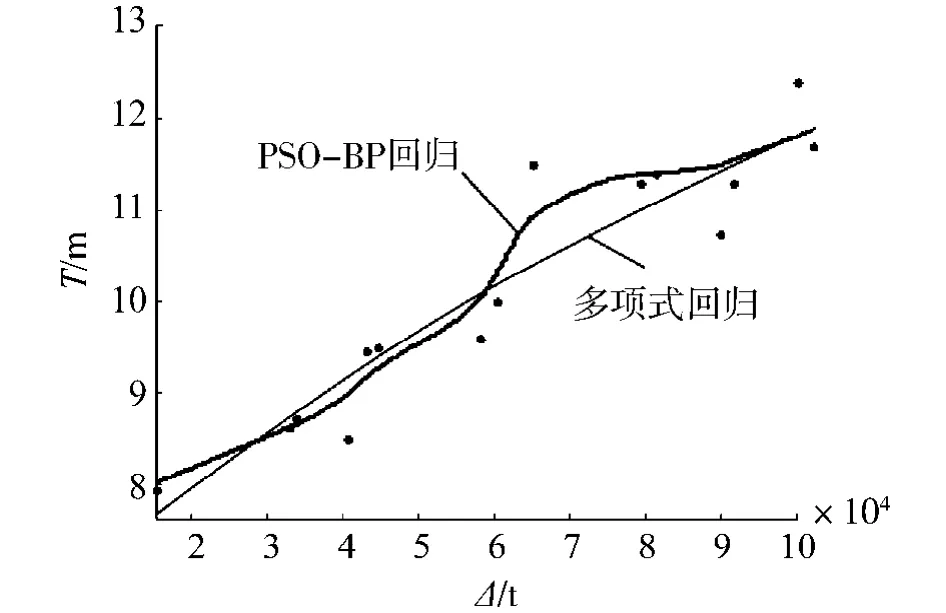
图6 吃水T与满载排水量Δ的多项式与PSO-BP回归Fig.6 Polynomial and PSO-BP regression of T and Δ

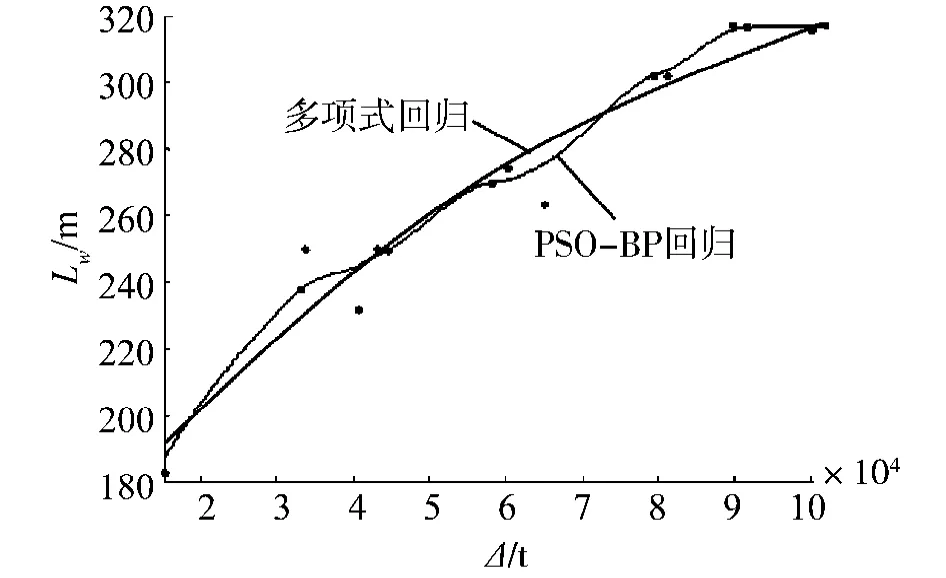
图7 设计水线长Lw与满载排水量Δ的多项式与PSO-BP回归Fig.7 Polynomial and PSO-BP regression of Lw and Δ

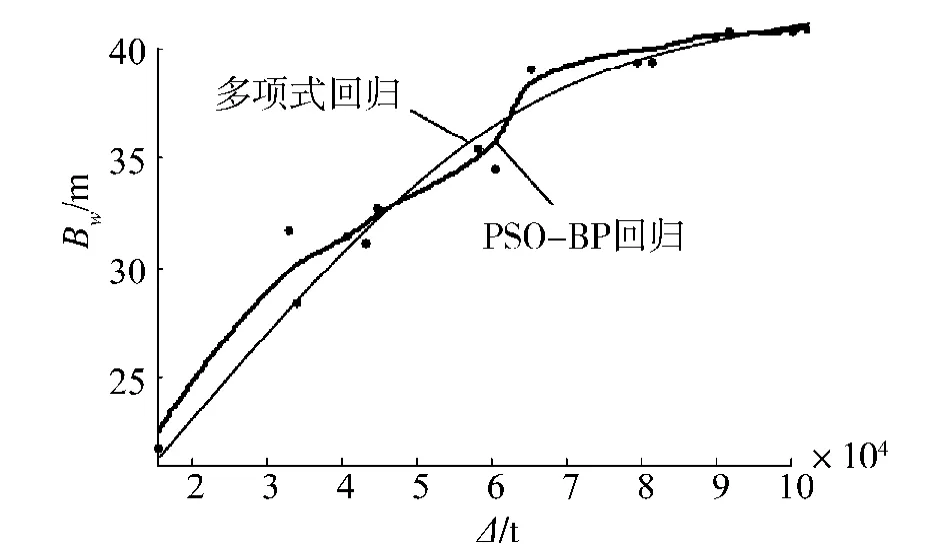
图8 设计水线宽Bw与满载排水量Δ的多项式与PSO-BP回归Fig.8 Polynomial and PSO-BP regression of Bw and Δ

3 结果分析与比较

对以上2种回归结果进行误差总结分析，引入用于评价数据变异性方面是否成功的衡量指标样本决定系数R2进行拟合优度评价［2］.R2即响应数据yi与预测响应数据之间相关系数的平方，其定义为回归平方和SSR与总平方和SST的比值.R2可以取0到1之间的所有值，值越接近1，拟合效果越好.表2为拟合曲线的拟合优度统计结果.

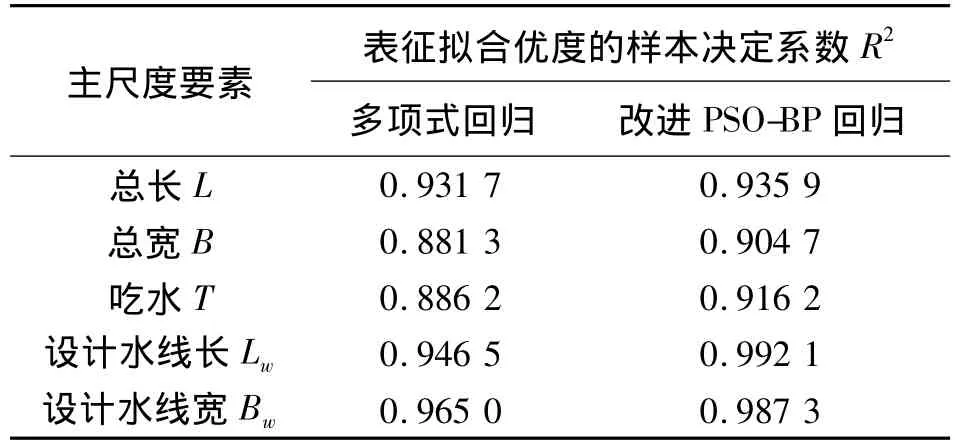
表2 2种方法的拟合误差统计结果Table 2 R2 of the two methods to comparison

从比较结果可知，用改进PSO-BP神经网络回归的精度要高于多项式回归.但前者没有明确的函数公式关系.针对光滑度而言，改进PSO-BP回归曲线的整体光滑程度不及多项式回归曲线，但具有良好的分段光滑特性，这在分析数据的分段变化趋势中具有非常重要的意义.

总体来说，2种方法的拟合值均较精确，误差满足设计精度要求.多项式回归曲线总体光滑，且可以给出回归公式，运用方便;改进PSO-BP神经网络回归曲线则更精确，具有良好的分段光滑特性.二者均可用于船型总体论证与初步方案设计.

4 结论

本文搜集国外典型航母的主尺度相关数据，将粒子群优化算法进行改进并引入到BP神经网络中，分别建立了多项式回归模型以及改进PSO-BP神经网络回归模型，并将回归分析误差进行比较，较好地拟合了主尺度关于满载排水量的变化规律.并得出以下结论:

1)对传统粒子群算法的学习因子进行关于迭代进程的自适应调整，这样有利于算法收敛于全局最优解，提高算法收敛速度和精度.

2)用改进PSO替换神经网络的BP学习算法，并构建新的粒子群神经网络模型，可以提高混合型神经网络的学习速度，并降低算法对网络初始权值的敏感性而减小网络受外界激发的震荡，加强算法的全局搜索能力.

3)本文为船舶主尺度数学模型的建立提供了一种新的思路和方法，将以往须通过分类拟合的项目整合，既能在回归自变量全范围内实现根据数据趋势自动分段，又保证在分段内部具有光滑特性.并通过对比实验证实了新方法的可靠性，该研究成果不仅具有相应的科学理论价值，而且具有重要的工程指导意义.

［1］邵开文，马运义.舰船技术与设计概念［M］.北京:国防工业出版社，2005:496-567.

［2］何晓群.应用回归分析［M］.北京:中国人民大学出版社，2007:135-145.

［3］BAYAR S，DEMIR I.Modeling leaching behavior of solidified wastes using back-propagation neural networks［J］.Ecotoxicology and Environmental Safety，2009，3(72):843-850.

［4］CLERC M，KENNEDY J.The particle swarm-explosion，stability，and convergence in a multi-dimensional complex space［J］.IEEE Transactions on Evolutionary Computation，2002，6:58-73.

［5］何佳，陈智慧，杨迎新.综合改进的粒子群神经网络算法［J］.计算机工程与设计，2008，29(11):2890-2896.HE Jia，CHEN Zhihui，YANG Yingxin.Integrative improved particle swarm optimization neural network arithmetic［J］.Computer Engineering and Design，2008，29(11):2890-2896.

［6］唐小勇，于飞，潘洪悦.改进粒子群算法的潜器导航规划［J］.智能系统学报，2010，5(5):443-448.TANG Xiaoyong， YU Fei， PAN Hongyue. Submersible path-planning based on an improved PSO［J］.Transactions on Intelligent Systems，2010，5(5):443-448.

［7］刘宏达，马忠丽.均匀粒子群算法［J］.智能系统学报，2010，5(4):336-341.LIU Hongda，MA Zhongli.A particle swarm optimization algorithm based on uniform design［J］.Transactions on Intelligent Systems，2010，5(4):336-341.

［8］HAGAN T，DEMUTH H，BEALE M.Neural network design［M］.Boston:PWSPublishing，2002:360-373.

［9］施彦，黄聪明，侯朝桢.基于改进的PSO算法的神经网络集成［J］.复旦学报:自然科学版，2004，10(5):692-694.SHIYan，HUANG Congming，HOU Chaozhen.Neural network ensembles based on improved PSO algorithm［J］.Journal of Fudan University:Natural Science，2004，10(5):692-694.

［10］高海兵，高亮，周驰，等.基于粒子群优化的神经网络训练算法研究［J］.电子学报，2004，32(9):1572-1574.GAO Haibing，GAO Liang，ZHOUChi，etal.Particle swarm optimization based on algorithm for neural network learning［J］.Acta Electronica Sinica，2004，32(9):1572-1574.

［11］方冬革.航空母舰发展史及航空母舰对世界的影响［M］.上海:科学技术文献出版社，2009:103-477.

［12］孙诗南.现代航空母舰［M］.上海:上海科学普及出版社，2000:182-236.

［13］WILAMOWSKI B M.Neural network architectures and learning algorithms［J］.Industrial Electronics Magazine 2009:56-63.

［14］董长虹.Matlab神经网络与应用［M］第2版.北京:国防工业出版社，2007:64-90.