膨胀节成型机模糊自适应趋近律滑模控制研究

柳 波， 王 浩， 高 宇， 黄 杰

（1.中南大学 机电工程学院，湖南 长沙 410083；2.长沙中联重科起重机分公司 工程技术部，湖南 长沙 410131）

在膨胀节成型机中，电液比例系统提供压胀成型的机械传动机构所需的动力，其动态响应速度较快、工作稳定可靠。机器工作时，电液比例系统的参数会随工况的变化而变化，且需要克服一些未知的外界干扰，故该系统具有时变性和非线性等特点，系统难以获得优良的动态特性和稳态品质［1］。

滑模控制通过控制器结构的调整和变化，可以有效地控制具有参数变化和外部干扰的被控对象，对非线性系统显示出良好的控制特性［2］。实际应用中，抖振导致超调或快速性变差，甚至系统不稳定，造成低的稳态精度、机械谐振，影响控制效果。采用趋近律设计，可以不对输出限制结构，具有结构简单、品质优良的特点［3］。

将模糊控制与趋近律滑模控制理论结合构成自适应趋近律模糊滑模控制器，可有效减弱或消除变结构系统的抖振并提高系统的响应速度。本文采用基于指数趋近律的模糊自适应滑模控制。

1 结构与工作原理

膨胀节成型机由液压驱动，采用阀控缸的控制形式，液压位置控制系统由控制器、电液比例阀、液压缸、负载以及位置传感器等组成，液压缸驱动机械传动机构，机械传动机构由传动锥和模具组成，传动锥垂直向上运动，通过锥面推动模具水平运动，挤压管坯成型。传动锥的锥度为θ，因此机械传动机构的传动比n＝tanθ。膨胀节成型机结构如图1所示。

图1 膨胀节成型机液压系统及结构示意图

2 电液比例控制系统的数学模型

根据流量的连续性，液压缸工作腔的流量方程为：

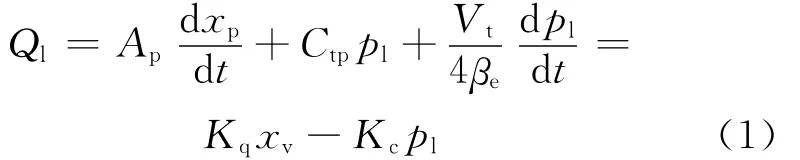
其中，Ap为液压缸活塞面积；Ctp为液压缸总泄漏系数；βe为有效体积弹性模量；xp为液压缸活塞位移；pl为进、回油腔压力差；Vt为工作腔的总容积；Kq为流量增益；Kc为流量－压力系数。

控制信号和阀芯位移的关系式为：

其中，xv为阀芯位移；Kv为放大器增益；Ki为比例阀增益；u为输入电压。

因机械传动机构传动比n＝tanθ，故（1）式可改写为：

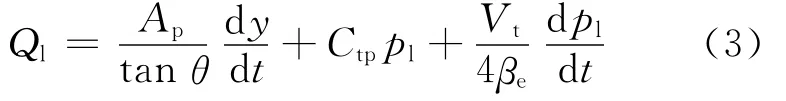
其中，y为模具位移。

负载力平衡方程为：

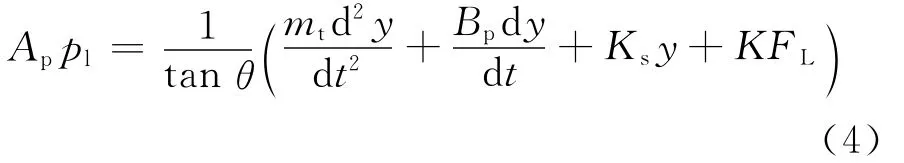
其中，mt为活塞及负载折算到活塞上的总质量；Bp为活塞及负载的黏性阻尼系数；K为负载弹簧刚度；FL为作用在活塞上的任意外负载力；Ks为弹簧系数。

取系统状态变量为x＝［x1，x2，x3］T，其中，，则系统的状态空间方程为：

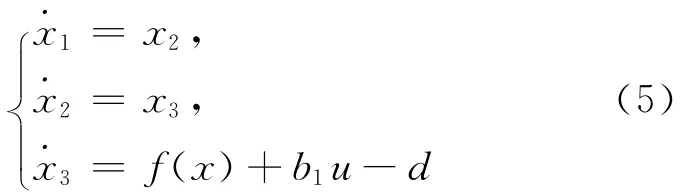
其中，f（x）＝－a1x1－a2x2－a3x3，且有：

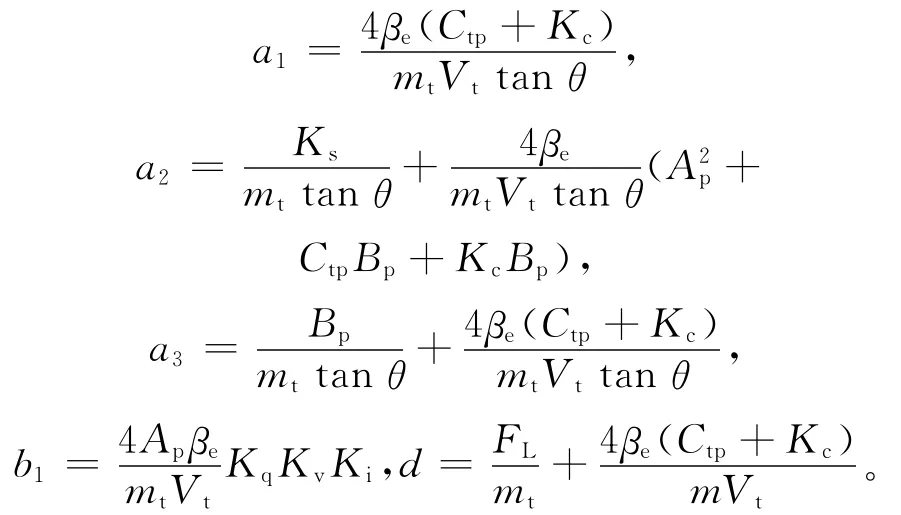
电液比例系统具有本质非线性的特点，同时系统负载的变化、外界干扰变化、温度变化引起的液压油弹性模量和黏性系数的变化等使得系统具有不 确 定 性，因 此 a1、a2、a3、b1、d 都 是 不 确定的［4］。

3 控制器的设计

在系统参数不确定的条件下，设计滑模控制器使系统的输出y跟踪期望输出信号yd，定义系统误差为e1＝yd－y。

定义切换函数为：

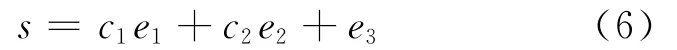
则有：

采用指数趋近律并构造：

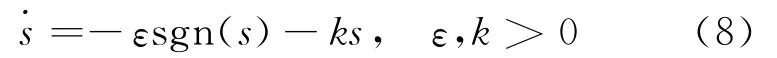
则有：

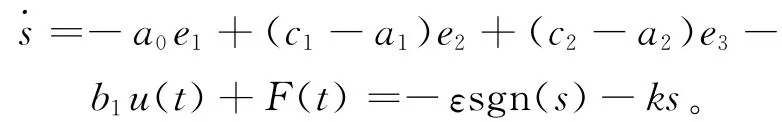
解得输出：

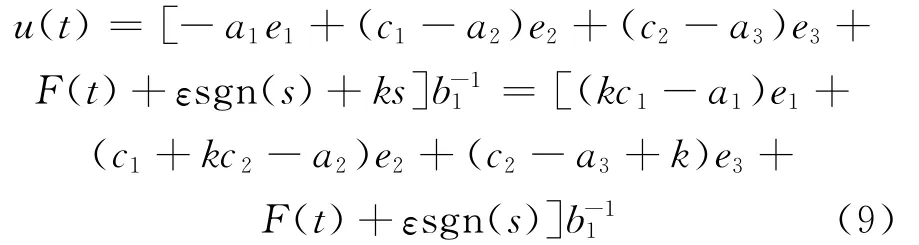
构造Lyapunov函数进行稳定性分析，V＝s2／2，则有：

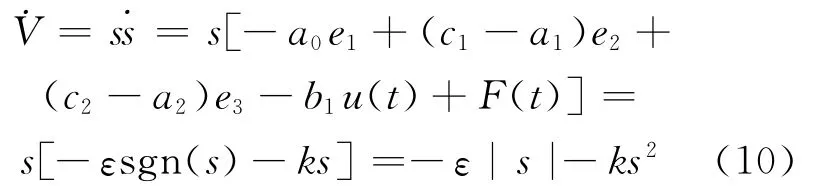
因此可知˙V＜0。故存在滑动模态区，系统是稳定的［3－7］。

系统参数变化范围较大，需要选取较大的ε以保证系统滑动模态的存在以及系统的鲁棒性，从而增加系统抖振，影响系统性能。为此，本文采用模糊逻辑规则自适应调整ε的大小，保证系统具有良好的性能。

模糊自适应指数趋近律的结构：设计二输入、单输出的2位模糊控制器，取切换函数s（x）及其变化率（x）为输入，反应系统抖振指标的ε为输出，其中

确定对应模糊论域为：

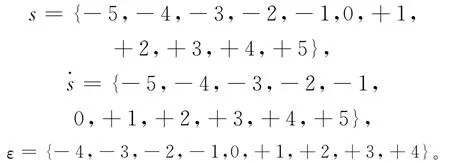
输入／输出隶属函数形式为：

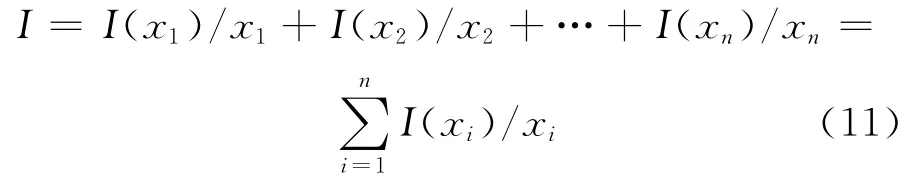
根据律属度函数滑模控制器使用25个模糊规则，每条规则都给出一个F蕴涵关系Ri（i＝1，2，…，25），这25个F蕴涵关系Ri的并构成系统总的模糊蕴涵关系R［10－11］，即

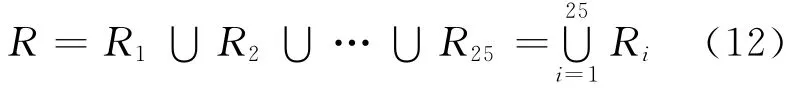
将R代入近似推理合成法则得：

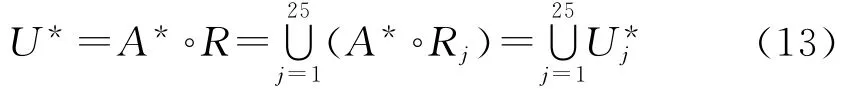
其中，U＊为输出量，＝A＊◦Rj。采用最大隶属度平均值法解模糊，设A（uj）＝max A（u），j＝1，2，…，n，则系统输出为

4 仿真研究

将本文研究的膨胀节成型机位置控制系统趋近律模糊滑模控制算法，建立图2所示的膨胀节成型机液压系统Simulink控制模型，和PID算法进行比较，通过计算机仿真对其正确性和有效性进行验证。假设系统期望位置输出信号为：yd＝0.05sin t。PID控制的参数为：Kp＝10，Ki＝30，Kd＝0.1。指数趋近律模糊滑模系统参数：Ap＝1.53×10－3m2，mt＝250kg，Vt＝0.107N／m2，Bp＝8.8×10－5N·s／m，βe＝7×108N／m2，Kc＝4.35×10－12m3／s·Pa。

通过计算得到：a1＝18.2×107，a2＝1.85×106，a3＝113.8，b1＝4×108，d＝0.46FL＋0.004˙FL，c1＝24 336，c2＝221。

图3a所示为系统跟踪yd＝0.05sin t的10s响应曲线，图3b所示为系统跟踪yd＝0.05sin t的3s响应曲线，可以看出PID控制的响应峰值比期望峰值高出0.03m，时滞约为0.1s，而趋近律模糊滑模控制线响应峰值几乎和期望峰值相同，同时时滞很小。图4所示为跟踪yd＝0.05sin t的10s误差曲线，可知趋近律模糊滑模控制线误差下降较PID控制线迅速，并且抖动很小，最大误差不足PID控制的误差的1／10。图中EXPCT为期望输出，PID为PID输出，FSMC为模糊滑模控制输出。

图2 膨胀节成型机液压系统Simulink控制模型

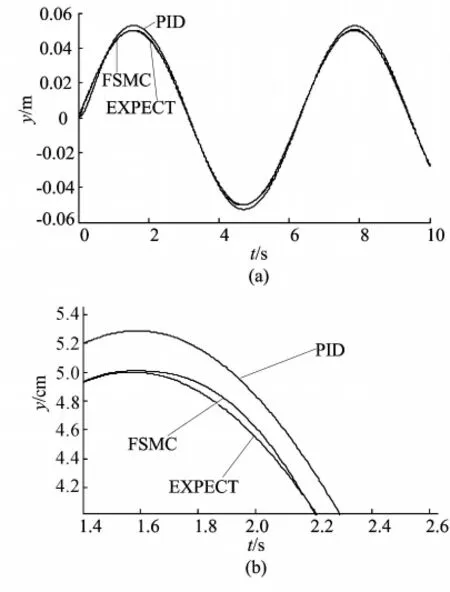
图3 跟踪yd＝0.05sin t信号的响应曲线

图4 跟踪yd＝0.05sin t信号的误差曲线

5 结束语

本文针对某膨胀节成型机电液比例位置控制系统容易受系统参数不精确和其他因素影响导致精度降低和抖振的缺点，引入模糊自适应趋近律滑模控制方法，对系统分别进行PID和趋近律模糊滑模仿真进行比较，仿真结果表明，该方法较PID控制精度大幅提高，实现了平滑抖振，达到了系统的精度要求，同时保持了传统滑模控制良好的鲁棒性能，提高了膨胀节成型机的性能。

［1］ 靳宝全，熊诗波，梁义为.考虑反馈机构动刚度的轧机伺服压下系统建模与仿真［J］.中国机械工程，2008，19（11）：1330－1335.

［2］ Akbarzadeh T，Shahnazi R.Direct adaptive fuzzy PI sliding mode control for a class of uncertain nonlinear systems［C］／／Johnson M.IEEE International Conference on System，Man and Cybernetics.Hawii：IEEE Press，2005：1 058－1 061.

［3］ 靳宝全.基于模糊滑模的电液位置伺服控制系统［M］.北京：国防工业出版社，2011：46－97.

［4］ 白 寒，管 成，冯培恩.电液比例系统变论域自适应模糊滑模控制［J］.电机与控制学报，2009，13（5）：728－734.

［5］ Wang Danwei，Xu Guangyan.Full－state track－ing and internal dynamics of nonholonomic wheeled mobile robots［J］.IEEE ASME Tran－sactions on Mechatronics，June.2003，8（2）：203－214.

［6］ Ramos M C，Koivo A J.Fuzzy logic－based optimization for redundant manipulators［J］.IEEE Transactions on Fuzzy Systems，Aug.2002，10（4）：498－509.

［7］ 段锁林，王明智.自学习模糊滑模控制及其在电液伺服系统中的应用［J］.机械工程学报，2004，40（3）：162－167.

［8］ 谷玉凯，杨滁光，王华强，等.基于模糊神经网络分类器的精馏塔温度控制器设计［J］.合肥工业大学学报：自然科学版，2012，35（1）：41－44，137.

［9］ 刘金琨.滑模变结构控制 MATLAB仿真［M］.北京：清华大学出版社，2005：116－143.

［10］ Karnopp.Computer simulation of stick slip friction in mechanical dynamic systems［J］.Journal of Dynamic Systems，Measure－ment and Control，1985（4）：100－103.

［11］ 付永领，王 岩，逢 波.滑模模糊控制算法在液压机器人控 制 中 的 应 用 ［J］.中 国 机 械 工 程，2007，18（10）：1168－1170.