基于实测数据的稀布阵雷达副瓣对消研究

郑 禹， 汪 萍

（安徽建筑工业学院 机械与电气工程学院，安徽 合肥 230601）

随着电子技术的不断发展，雷达要在日益复杂的电子对抗环境中仍能发挥作用，需要具备有效的电子对抗和反对抗措施。一般雷达难以靠天线波束的低副瓣消除副瓣有源干扰的影响，必须在信号处理中采用有效的措施来抑制旁瓣干扰。目前的主要方法有自适应波束形成（ADBF）和自适应旁瓣相消（SLC）2种方法［1］。对于工作在米波频段的雷达来说，遇到的有源干扰较多，所以在本机系统中采用哪种方法来抑制干扰尤为重要。因为本机系统为100路接收天线信号，直接作自适应波束形成的运算量较大，无法实时实现。为了减少运算量，需采用快速ADBF算法，但快速算法都需要事先知道干扰源的个数，最重要的是需要已知阵列流形，且对误差十分敏感。所以本文采用SLC技术，结合具体工程实际对干扰对消中的对消性能进行分析。

1 综合脉冲孔径雷达干扰对消原理

自适应天线旁瓣相消技术采用辅助天线，将它所接收的信号与主天线接收的信号加权求和，目的是在干扰作用下，利用其输出调整权值，使输出干扰功率趋于最小，其结果是使空间滤波器特性在干扰方向上形成空间零点，从而抑制了旁瓣干扰［2］。以一个单频干扰为例，主、辅天线会接收到振幅、相位不同的干扰信号，辅助支路的复权调整其干扰信号的振幅、相位，使之与主支路的干扰信号相抵消。随着干扰源方向的改变，两路干扰信号的振幅和相位也随之变化，所以权值的调整必须是自适应的，使空间零点一直对准干扰源的方向，因此称之为自适应天线旁瓣相消。显然，在自适应旁瓣相消系统中最为重要的、也最富有变化的就是权值估计部分，也就是求解自适应最优权值的算法和实现结构。在数字开环自适应旁瓣相消系统中求解最优权多采用最小二乘算法，这是目前自适应算法研究的发展趋势，因为最小二乘算法为全局最优的近似算法。所谓开环处理就是直接地或间接地通过解样本Wiener－hopf方程R W＝b来获得最优权值，并作加权对消，其中，［W1，W2，…，Wn］T；x（ti）＝［x1（ti），x2（ti），…，xn（ti）］T；xk（ti）为第k个辅助通道在第i次采样的输入样本数据；d（ti）为主通道在第i次采样的输入样本数据；M为估计用的样本数目。

本文描述的稀布阵雷达［3－4］具有稀疏阵列分布体制的特点，其方位副瓣一般较差，在－20dB左右，易受方向副瓣干扰，为了使系统稳定可靠地工作，干扰对消技术的运用对此雷达体制来说是非常必要的。在此需要指出的是，综合脉冲孔径雷达试验系统为多通道阵列处理，其主天线信号应为对多通道进行DBF合成的信号，区别于常规雷达，不需要另外增加辅助天线，只要从正常工作的100路接收天线信号中抽出几路信号作为辅助天线的信号即可。考虑到本机系统最多可对消5个干扰信号，分析时从天线中抽出大致等间隔分布的10个天线作为辅助天线，这10个天线也同时用于信号的DBF处理。快拍数选择需要满足干扰信号估计的平稳性，从系统硬件实现能力上考虑，试验选取快拍数为64快拍。

2 对消性能影响分析

2.1 计算精度影响

系统副瓣对消功能的硬件实现是在ADSP201器件里实时进行对消系数的计算，再将系数送入FPGA进行副瓣对消的运算。在副瓣对消调试过程中发现对消后的结果有起伏，而且对消比不能完全满足指标要求。DSP计算出的对消系数与Matlab计算出的系数相比误差较大。而使用产生的随机数进行验证，DSP程序本身功能完全正常，应是DSP的浮点运算精度不够限制了副瓣对消的效果。因为各个辅助通道之间随机数没有相关性，而实际各路数据之间有很强的相关性，造成了DSP浮点运算计算对消权系数时精度不够［5］。

副瓣对消运算主要包括复数矩阵求逆和复数矩阵乘法等。改进DSP处理程序将运算进行64位浮点精度的改造。经过改进，DSP计算出的对消系数同Matlab仿真的结果已经相当接近，对消系数的幅度比值在0.95～1.02之间，如图1所示。

为了比较，图2给出了64位和32位精度时Matlab仿真同DSP计算的对消系数的相位差值。

可以看到与64位精度相比，32位精度计算出的对消系数同Matlab仿真结果相比差异较大，64位精度时，相位差值在－1.5°～7.8°之间，均方根为2.731 6°；而32位精度时相位差值在－7.2°～9.0°之间，均方根为4.756 9°。

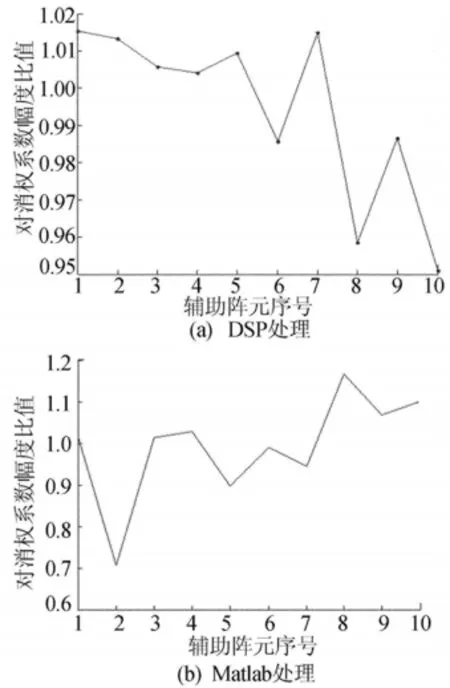
图1 64位精度实时处理和Matlab处理幅度比

图3a给出了64位浮点精度同Matlab仿真计算出的最终对消结果。可以看到两者非常吻合而且对消比大于40dB，这说明64位DSP计算完全能够达到指标。

图3b给出32位浮点精度计算结果，同Mat－lab仿真结果相比32位浮点精度对消结果差28dB左右。因为不是同一时段采集的数据，2张图上的数值有所差异，但仍然能说明问题，即Matlab仿真结果对消比仍然大于40dB，而32位精度的对消结果只有25dB左右。

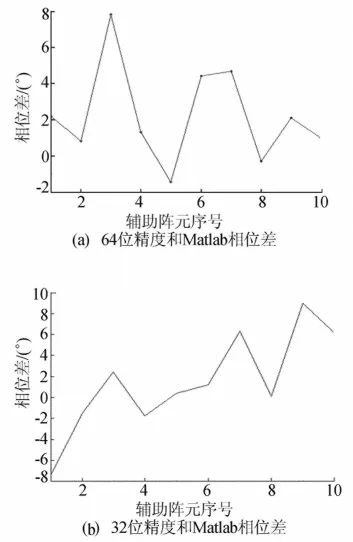
图2 对消系数DSP实时计算和Matlab仿真相位差

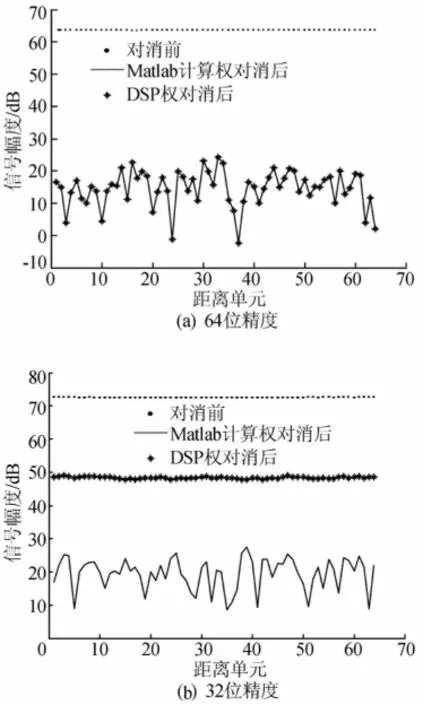
图3 DSP处理和Matlab仿真对消结果

2.2 干扰起伏性能影响

理论上干扰对消应是实时实现的，但在工程实现中一般在前一个CPI的某个脉冲的休止期采集干扰数据，储存起来给下一帧做对消。在干扰起伏的情况下，此方法对消会有起伏。图4给出了干扰起伏对干扰对消影响的仿真试验结果。

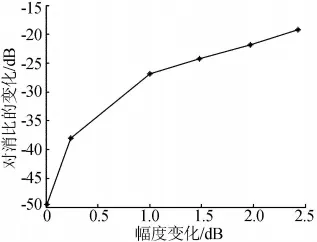
图4 干扰对消比随干扰幅度帧间变化

图4为仿真远场点频干扰，表明帧间幅度变化对消性能影响较大，为此需要对干扰对消权计算程序进行处理速度优化，将每个对消权计算仅分配数个脉冲重复周期的时间，增加其实时性，以减少干扰幅度起伏的影响。

2.3 采样点位置影响

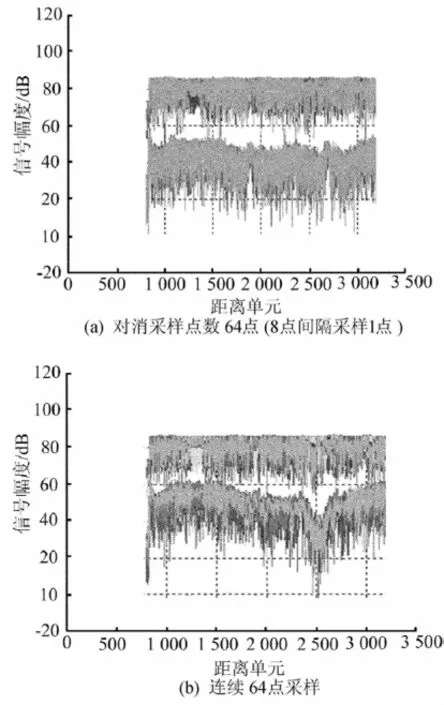
图5 对消点数取样影响

图5给出3个方向干扰源（2个调频干扰，1个点频干扰）的数据分析。在实际采集的数据中，由于3个干扰源的幅度起伏，采集到干扰信号平稳性较差，此时在硬件存贮能力固定的情况下（64点），如果连续采样64点，信号对消后起伏较大，间隔8点采样干扰数据进行对消，对消信号后信号更加平稳。

2.4 采样点位置影响对多点频信号的干扰

在利用信号源工作于单点频模式，模拟单点频干扰时，发现系统干扰对消效果很好，可以将干扰稳定地对消至噪声的幅度水平，但双（多）点频干扰时对消起伏很大，且干扰对消效果和信号频差有关。

图6给出了双点频干扰条件某路接收机接收的干扰数据原始幅度在不同频差条件下的仿真。由图6可见在点频干扰情况下，由于各信号源的单点频信号产生干涉叠加的效果且信号干扰源频差不一样，回波干涉调制的周期也不同。在采样快拍64点的情况下，信号源频差在10Hz～10kHz之间时信号干扰幅度估计无法平稳，故干扰起伏大，在信号源频差小于10Hz或大于10kHz的情况下，计算干扰对消权时，干扰估计的幅度较平稳，能达到理想干扰效果，这与双点频信号干扰源的实验结果也是基本吻合的。

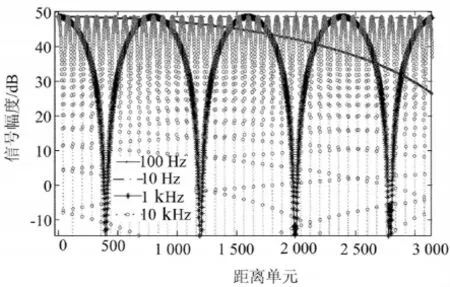
图6 双点频不同频差时干扰原始数据幅度仿真

3 试验仿真结果对比

在远场放置单点频干扰源，给出单点频试验的Matlab和DSP处理结果，图7所示为DSP64位运算结果（通过Matlab和Quartus II的SignalTap工具互联实时获取处理对消结果），图8所示为Matlab非实时处理结果。

对比图7、图8可知，对同一个波位（方位0°，仰角0.3°），Matlab处理和DSP实际处理的对消比稳定均在40dB，处理后的噪声起伏结果一致，可见DSP64位运算处理可以满足系统要求。

4 结束语

本文对综合脉冲合成孔径雷达干扰对消特点进行了分析，并通过实验证明采用此干扰对消方法可成功完成对多个干扰源的抑制。研究表明由于阵列接收信号间的强相关性，干扰对消对计算精度要求很高，32位浮点精度在多路辅助通道副瓣对消中的精度则达不到要求，64位浮点精度的对消效果要好于32位精度，同Matlab仿真的结果非常吻合；在干扰幅度起伏严重的情况下准实时干扰对消性能存在损失，需要改进处理算法，实现脉冲重复周期内实时对消。

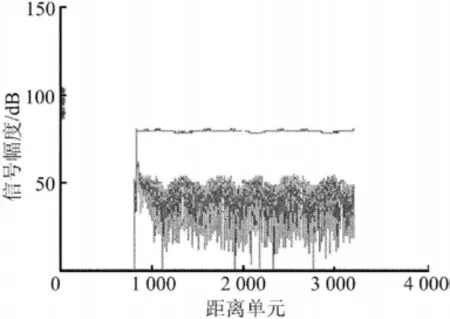
图7 DSP实时处理数据结果

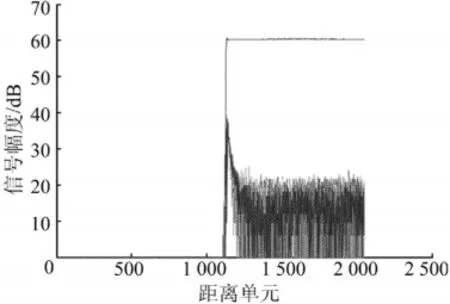
图8 Matlab非实时处理结果

［1］ 徐海洲，吴曼青.数字阵列雷达系统［J］.合肥工业大学学报：自然科学版，2008，31（5）：718－720.

［2］ Nitzberg R.Effect of errors in adaptive weights［J］.IEEE Transactions on Aerospace and Electronic Systems，1976，AES－12：369－373.

［3］ 吴剑旗，贺瑞龙，江 凯.稀布阵综合脉冲孔径雷达的研究与试验［J］.现代电子，1998，6（3）：1－5.

［4］ 陆鹏程，徐海洲，徐 晋.稀布阵综合脉冲孔径雷达阵列优化设计［J］.雷达科学与技术，2008，6（4）：243－246，260.

［5］ 王晓军，李 侠，吴铁平.辅助通道HT变换法及其在旁瓣对消中的应用［J］.系统工程与电子技术，1999，21（11）：26－28.