最优生产批量模型的理论缺陷及其改进

邢如其， 崔 笑， 李 伟， 张 如， 臧 云

(石家庄铁道大学经济管理学院，河北 石家庄 050043)

一、引例

假设某公司全年生产甲零件，已知全年生产量36 000个，生产每批零件的调整成本1 000元，全年平均储存成本2元/件年，每天生产量300件，每天发出(或领用)量200件，企业将如何安排生产才能使总成本最低？显然，这是一个最优生产批量的决策问题。应用最优生产批量模型：

最优生产批量

(1)

最优生产批量的全年总成本

(2)

式中，A为零部件(或产品)全年生产量；Q为零部件(或产品)生产批量；TC为最优生产批量的总成本；S为生产每批零部件(或产品)的调整成本；C为每个零部件(或产品)的全年平均储存成本；q为零部件(或产品)的每天生产量；d为零部件(或产品)的每天发出(领用)量。

可得最优生产批量Q*≈10 392件，最优生产批次n=A÷Q=36 000÷10 392 ≈ 3.5批，最优生产批量的总成本TC≈ 6 928元。实际上，这个结果是错误的，可由下面的逐次测试得以证实(如表1所示)。

应用逐次测试法，最优的经济批量、批次和最低成本分别为14 697件、2.5批和4 950元，而不是10 392件、3.5批和6 928元。

为什么会出现这样错误的结论呢？原因在于模型(1)、(2)隐含了一个假设。即一年的生产量与发出量之比为一年(一年按360天计，下同)，如果实际情况不满足此假设，就将导致错误的决策。

如果在上例中，每天甲零件的发出量不是200件，而是100件，则应用模型(1)、(2)可得：最优生产批次n=A÷Q=36 000÷7349≈4.9批，最优生产批量的总成本TC≈9 799元。这个结果是正确的，因为，每天发出100件，36 000件正好是一年的发出量。这个结果和下面的逐次测试法得到结果一致，如表2所示。

企业在实际的生产批量决策中，一年的生产量与发出量之比恰好等于360的情况是不多见的，这就需要对模型(1)、(2)进行修正[1-2]。

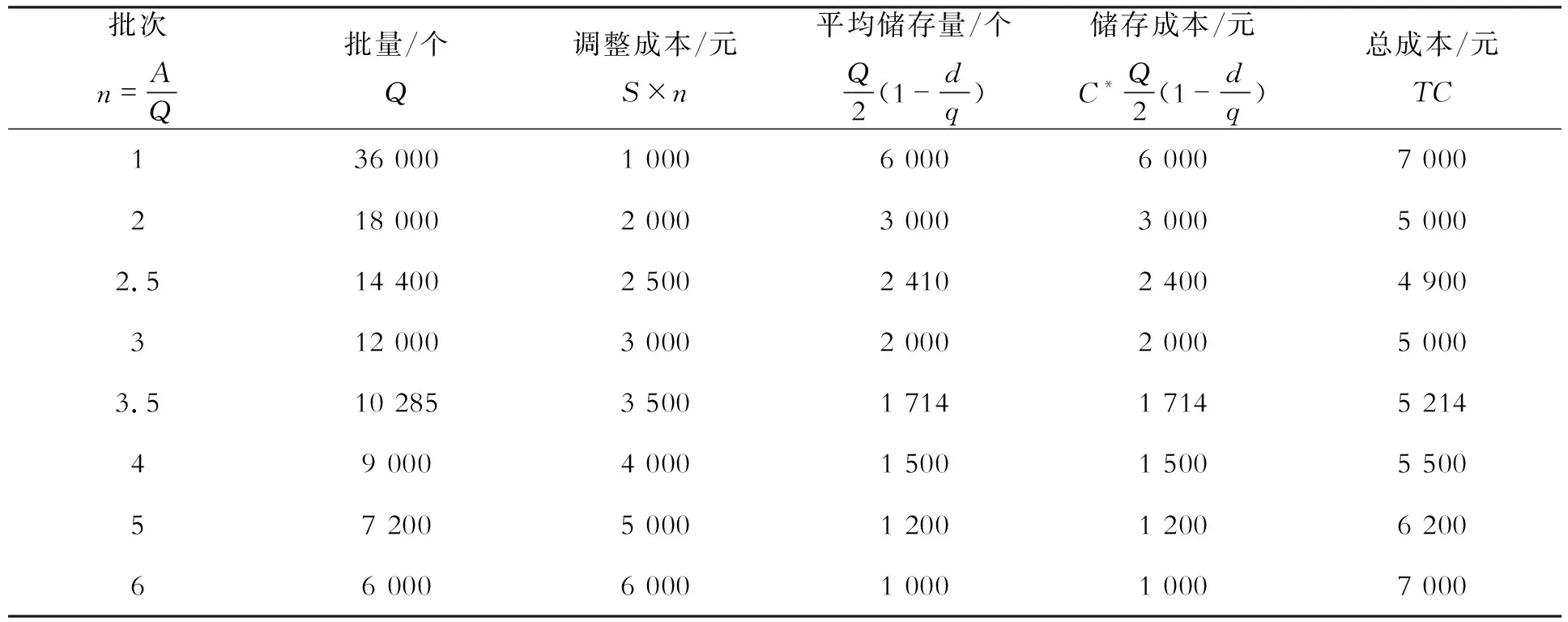
表1 每天发出200件时的最优生产批量

注：表1中的单位储存成本是按1元计算的。

表2 每天发出100件时的最优生产批量

二、单一产品经济生产批量模型改进

在每天发出200件时，表1中逐次测试的结果显示最优批量为14 400件，2.5批，此时的成本为4 900元，而不是利用(1)、(2)式计算的3.5批。原因是每天发出200件，存储甲零件的最长时间是：36 000÷200=180天，只有半年，存储成本就应当按半年计算，而不能按一年计算。也就是每个零件的储存成本C*=2÷360×180=1元/件。

在零部件存储时间不足一年的条件下，如果仍然应用类似(1)、(2)形式的模型，需要对其进行改进[3]，只需将单位储存成本C假设一年改为平均每天储存成本不受生产数量与发出量之比必须为360的限制。此时：

调整成本=每次调整成本×调整次数，即

(3)

储存成本=单位储存成本×平均储存量×储存天数×批次，即

(4)

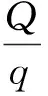
总成本=调整成本+储存成本

(5)

根据总成本TC最小的必要条件

(6)

可得，经济生产批量为

(7)

由Q*代入(5)可得

(8)

仍然沿用M公司生产甲零件的数据，如果每天发出量为100件，则：

=7 349(件)

≈9 798(元)

计算结果与原来的计算结果表2逐次测试结果一致。

如果每天发出量不是100件，而是200件，则：

=14 697(件)

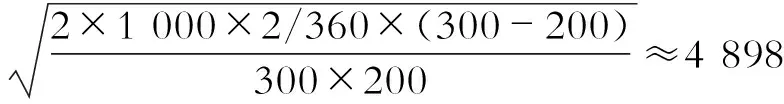
计算结果与原来的计算结果并不相同，但却与表1逐次测试的结果一致(表1中2.5批时的最低成本为4 950元，和4 898相差52元，是由于最优批次为一位小数所致)。也就是说，(7)、(8)才是不受每天发出数量限制的最有生产经济批量的决策模型。

三、多品种产品经济生产批量的确定

当企业用同一种生产设备轮换分批生产多种产品或零部件时，有人主张采用共同最优生产批次模型来确定生产批量，此时的模型为

(9)

(9)式中，各符号的含义与(1)、(2)中的含义相同。

实际上，由(9)所确定的共同最优批次并不能保证总成本最低，即不存在共同最优生产批次。比如，N企业生产甲、乙两种产品，有关两种产品的数据如表3所示：

表3 N企业生产甲、乙两种产品有关数据资料

根据表3资料和(9)得：

=3.539(批)

由此可得：

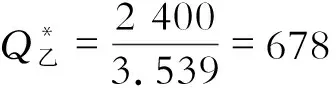
根据(2)得：

TC甲=4 157(元)，TC乙=2 351.5(元)；

总的成本

TC总=TC甲+TC乙=6 508.5(元)

而根据(7)、(8)可得：

总的成本

TC总=TC甲+TC乙=2 400+1 920=4 320(元)。

由此可知，应用共同最优生产批次所得结果，较之应用(7)、(8)要多花费成本2 188.5(6 508.5-4 320=2 188.5)元。也就是说，应用(9)所确定的“共同最优生产批次”的计算公式，不能实现多种产品在同一设备轮换生产的最优，也就是不存在多种产品的“共同最优生产批次”。只能应用(7)、(8)确定每种产品的最优批量和批次后，再统筹安排轮换生产才能实现最优。这个论断可以根据证明(5)、(6)的原理，并应用解析法得到证明。

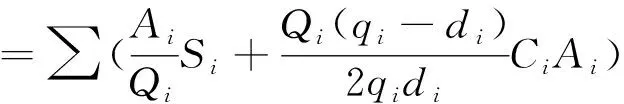
(10)

由于(10)中各产品的批量Qi和Qj没有相乘的关系，当TC总对Qi求偏导时，任意的Qj(i≠j)均为常量。所以：

(11)

由(11)很容易地即可得到(5)、(6)，进而得到(7)、(8)。