生活中的数学问题

王锟

(广东科技学院 基础部，广东 东莞 523083)

生活中的数学问题

王锟

(广东科技学院 基础部，广东 东莞 523083)

从数学角度分析生活中的各种常见问题，尝试用数学思维来推理其详细过程及结果，旨在能更充分的理解问题的本质及过程，让大家能深层次地认识现象，也希望通过这种数学思维的不断锻炼来解决更多的生活难题。

生活问题数学化;存款;贷款;个人所得税

在越来越喜欢上网百度各种答案的今天，很多人越来越不重视解决问题的思路和过程，只在乎结果。我们现在有些教育也是这样，仅仅告诉学生最后的公式或者结果，而不详细解释为什么会有这样一个公式或结果的产生。其实，以数学教育为例，生活中有很多问题可以用数学思维来推理和解决，我们在教育学生的时候，不仅仅传授的是数学知识，还要培养学生应用数学的意识，让学生渐渐学会用数学思维来思考和理解周围的事物，用数学方法来解决和分析遇到的生活问题。著名数学教育家H.弗洛登塔尔(Freudenthel，Hans)指出:“数学源于现实，并且用于现实”，这是一个值得欣赏的观点。当然，从生活中的问题到用数学解决这些问题并不是一件简单的事情，要有意识地不断地培养、训练和实践。下面将用数学思维详细地解释和推理几个生活中常见的问题。

一 存款问题

存款是常见行为，几乎大部分人都去过银行存款或者拥有存款，可是有多少人留意过存款所产生的利息(目前暂无需交利息税)，利息因存款额和存款时间的不同而不同，利息是怎么计算的?钱存入银行被很多人认为是一种最安全的投资，那么如果存一笔数额较大的钱在银行一段时间，能够产生多少利息呢?这是很多人关注的的问题。现如今银行计算存款都采用单利计算的方式，下面将详细分析存款所得利息的思路及过程。

现设期初存入银行x元为本金，设银行年利息率为i，yi为第i年末本金和利息之和，则:

第一年年末除了期初已存入的本金x元外，还有本金在这一年中所产生的利息为x·i元，因此第一年期末的本金和利息之和y1=x+x·i=x(1+i)元;

第二年初始的本金仍然为x元不变，本金在这一年中产生的利息为x·i元，但是第二年期初已经有的上一年期末的x(1+i)元不变，因此第二年期末的本金和利息之和

y2=x(1+i)+x·i=x(1+i+i)=x(1+2i)元;

依此类推，寻找相应规律，可以得到第n期末的本金和利息之和为yn=x(1+ni)元。

例如:现期初存入银行20 000元本金，整存整取存定期两年，银行的年利息率为4.4%(根据目前银行最新利率表)，按照单利计算，请问两年后本金和利息之和为多少?

解:x=20 000，i=4.4%，y2=x(1+2i)=20 000(1+2 ×0.044)=21 760元

这就意味着这20 000元在这2年中产生了1 760元的利息，本金和利息之和可以得到21 760元。

其实按照单利计算对于广大的存款者并不公平，毕竟每期期末产生的利息广大的存款者并没有刻意地去取出来，也容易忘记取出来，所以这部分利息一般都继续存在银行中，但是这部分钱在以后的存款过程中并没有产生任何利息，仅仅是放在银行而已。因此会产生另外一种计算利息的方式，称为复利计算，按照复利计算利息的思路和过程如下:

第一年期末计算利息的过程同单利计算，本金和利息之和为y1=x+x·i=x(1+i);

第二年初始的本金变为x(1+i)元，新的本金在这一年中也将产生利息x(1+i)·i元，因此第二年期末的本金和利息之和y2=x(1+i)+x(1+i)·i=x(1+i)(1+i)=x(1+i)2元;

依此类推，寻找相应规律，可以得到第n期末的本金和利息之和为yn=x(1+i)n元。

例如:若上个例题中存入银行的20 000元，按照复利计算，请问2年后本金和利息之和为多少?

解:x=20 000，i=4.4%，y2=x(1+i)2=20 000(1+0.044)2=21 798.72 元

二 买房贷款问题(等额本息还款法)

现在很多年轻人买房，几乎很难承受高昂的房价，一般都是先付三成左右的首付，剩下的向银行贷款，以每月还银行部分款的形式买房。沉重的贷款往往会使很多年轻人感觉压力很大，分期付款的方式有利有弊，但是贷款者需要知道自己的承受能力，以免出现不能及时还银行贷款而产生滞纳金甚至供不下去的情况。所以购房者需要知道分期付款的思路，怎么计算贷款，而不是盲目的任凭房屋销售人员或者电脑计算程序帮忙计算，一个精明的理财者要知道钱是怎么花出去的，而不是将金钱掌控权放在别人手中。

接下来具体的分析买房分期付款的思路及过程，现设购房者向银行贷款y0元，银行贷款的月利息率为r(r=，i为年利息率)，还款期限为N个月，每月向银行等额还款x元，还款约定从借款的下一个月开始，于是在这一个月中，贷款的y0元产生了相应的利息y0·r元，开始还款的第一个月还银行x元后，还欠款y1=y0+y0·r－x=(1+r)y0－x;

第二个月还款x元后，还欠款y2=y1+y1·r－x=(1+r)y1－x;

第三个月还款x元后，还欠款y3=y2+y2·r－x=(1+r)y2－x;

依此类推，第N个月还款x元后，还欠款yN=yN－1+yN－1·r－ x=(1+r)yN－1－ x，且因还款期限为 N 个月，所以到此已经全部还完银行贷款，yN=0。从后往前推，这是一个特殊的差分方程，逐项代入过程及相应结果如下:yN=(1+r)yN－1－ x=(1+r)［(1+r)yN－2－ x］－ x=(1+r)2yN－2－ x(1+r+1)=(1+r)3yN－3－ x［(1+r)2+(1+r)+1］ =(1+r)Ny0－ x［(1+r)N－1+(1+r)N－2+… +(1+r)+1］=(1+r)Ny0－x·=0

而 (1+r)N－1+(1+r)N－2+ … +(1+r)+1 为首项是a1=1，公比q=(1+r)的前N项和SN，根据等比数列的前N项和公式，SN==

代入差分方程yN，得到(1+r)Ny0－x·=0，解得 x=

虽然计算的过程比较麻烦，特别是(1+r)N，高次方很难计算，有简便方法，打开电脑程序中的附件，选择计算器，在查看中找到“科学型”，运用x∧y即可很快计算出结果。

例如:小王2012年1月在东莞买了1套三居室，共花了80万，首付三成，剩下的向银行贷款，银行贷款的月利率为0.5%，贷款期限为20年，试问小王每月要还银行多少钱?

解:房款共计80万，首付了24万，向银行贷款56万，供房240个月，所以

y0=560 000，r=0.005，N=240

虽然只向银行贷款560 000元，但是因为月利息及贷款时间较长，因此实际上需向银行还款4 012×240=962 880元，其中利息就高达962 880－560 000=402 880元。

三 个人所得税的计算

作为公司普通的员工，每个月拿到工资条的时候，都会关注每一项所得以及扣款项目，其中个人所得税的扣款数额经常不一致，所以很多人都想知道到底扣税多少是如何计算的，虽然网上可以查到相应的税率和速算扣除数，但是扣税的详细过程又到底是如何呢?接下来，我们利用分段函数来给大家详细解释扣税的过程。

根据最新的从2011年9月1日起实施的扣税标准，以3 500元为起点共有7级超额累进税率，根据不同的月收入(扣除三险一金后)，有不同的税率，我们现设每月月收入为x元，根据x的大小分别予以分段讨论，如表1所示。

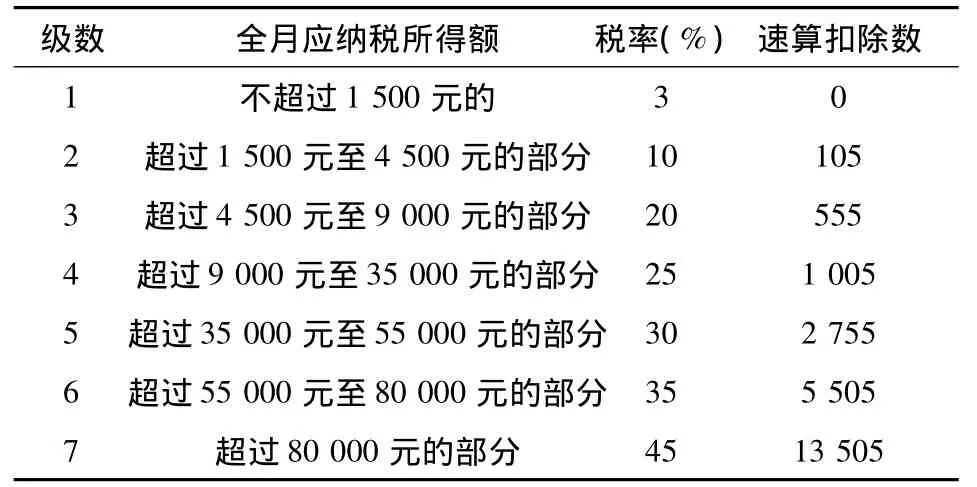
表1 个人所得税的计算方法

①若x低于3 500元，包括3 500元，即x≤3 500不用扣税;

② 若3 500＜x≤5 000，则比3 500元多的部分扣3%的税，即(x－3500)×3%;

③若5 000＜x≤8 000，则比5 000多的部分扣10%的税，即(x－5000)×10% 除此外，3 500－5 000元这部分也需按照3%扣税，所以这部分需扣(5 000－3 500)×3%=45元，共扣税(x－5 000)×10%+45元;

④若8 000＜x≤12 500，比8 000多的部分扣20%的税，即(x－8 000)×20%，除此外，3 500－5 000部分仍需扣45元，5 000－8 000部分按10%扣税，(8 000－5 000)×10%=300元，共扣税(x－8 000)×20%+45+300=(x－8 000)×20%+345;

依此类推，可以得到扣税分段函数如下:

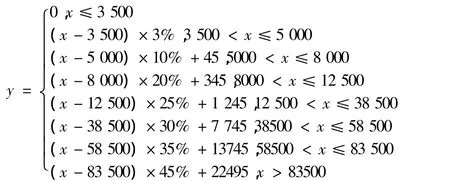
例如:小李2011年10月扣除三险一金后收入为9 000元，则他应交税多少?

解:因9 000元属于8 000＜x≤12 500这一段，所以代入公式有

(9 000－8 000)×20%+345=545元，应交税545元。

通过以上存款、买房贷款及个人所得税的过程分析，我们可以发现其实生活中的很多问题可以数学化，能利用数学思维和演算方式来解决这些问题。很多人都了解一些现象的表面，却从没有尝试着去理解现象的背后和深层，所以希望借助以上分析能让大家对这些经常遇见的问题有所了解，并能带动大家尝试用数学思维来分析和研究很多生活问题的积极性。

［1］李心灿.高等数学应用205例［M］.北京:高等教育出版社，1997.

［2］王 锟.函数的案例教学与教学案例［J］.考试周刊，2012，12(3):71 －72.

029

A

1674－5884(2012)07－0171－02

2012－04－11

王 锟(1983－)，男，湖南浏阳人，硕士，讲师，主要从事数学应用研究。

(责任编校 谢宜辰)