象山港围隔生态系水质模型研究

杨 红, 丁 骏, 王春峰, 陈 健, 刘成秀, 戴桂香, 赵 瀛

(上海海洋大学 海洋科学学院, 上海 201306)

象山港围隔生态系水质模型研究

杨 红, 丁 骏, 王春峰, 陈 健, 刘成秀, 戴桂香, 赵 瀛

(上海海洋大学 海洋科学学院, 上海 201306)

在美国环保局开发的WASP(the water quality analysis simulation program, 水质分析模拟程序)中的概念模型基础上, 运用系统动力学软件 Stella9.0.2建立了适用于海洋围隔生态系水质动力学模型。模型包括浮游植物、磷循环、氮循环、碳生化需氧量-溶解氧4个模块, 涉及叶绿素a、有机磷、无机磷、有机氮、氨氮、硝酸-亚硝酸盐氮、生化需氧量、溶解氧8个水质指标。利用2010年10月初象山港围隔生态实验数据进行了模型验证和参数率定工作, 成功模拟了不同水温条件下围隔水质情况, 并确定了 30余个模型参数, 展现了系统动力学模拟的优势, 为揭示象山港海域生态系统的动力学机制,模拟和预测他的变化提供科学依据。

象山港; 系统动力学; WASP(水质分析模拟程序); 水质动力学模型; 围隔生态系统

象山港是浙江省三大养殖基地之一, 对其水环境保护具有十分重要的现实意义。通过建立水质模型预测其水质状况不仅是水环境保护决策的依据,也是制订水污染综合防治规划及水环境保护规划的基础。目前, 应用较多的水质模型有： QUALⅡ[1]、MIKE21[2]、WASP(the water quality analysis simulation program, 水质分析模拟程序)[3]等, 但是此类模型多使用 FORTRAN或其他计算机语言编写, 众多参数和变量之间交互作用机制由于采用计算机语言编写相当复杂, 使用者不易了解。虽然开发者通过不断对其修订, 增加了模型的可视化操作界面, 并提高了其运行速度, 如USEPA改版的WASP7, 但因其源代码不公开[4], 给模型的二次开发和参数率定带来了很大限制。而系统动力学方法(System dynamics)[5-6]以逻辑学为建构基础, 运用图形作为沟通语言, 将变数间复杂的关系用库量(stock)、流(flow)和连接器(connector)等连接[7], 避免了WASP模型的复杂程序, 可操作性强, 通过方程式将各变量和其相关变量进行联系, 建立变量间的因果及回馈关系,这对于了解水质现象及反应过程大有裨益。另外, 模型的验证、改进和参数率定等是模型建立的关键, 除了借鉴国外海洋生态动力学模型外, 还应根据象山港海域海洋学和生态学特点, 通过现场实验等进行。其中, 海洋围隔生态实验由于具有生态系统可控、与海洋自然状况相近、时间连续等特点[8], 往往用以模型过程的研究以及相关生态动力学参数的测定[9-11],从而为模型的建立、验证、改进等提供了一个有效手段[12]。

本文通过系统动力学软件stella9.0.2[13-14]构建适用于海洋围隔生态水质动力学系统模型, 在参数率定后模拟结果与实测值之间有很好的吻合, 模型可用于象山港海域水质演变趋势预测, 为象山港海域的综合管理提供技术支持。

1 水质动力学模型

1.1 模型结构

本模型在美国环境保护局提出的水质模型程序WASP中的 EUTRO[3]四个模块基础上, 即浮游植物模块、磷循环模块、氮循环模块、CBOD-DO模块, 通过stella9.0.2构建浮游植物(PHYT)、有机氮(DON)、氨氮(NH4-N)、硝酸-亚硝酸盐氮(NO3/NO2-N)、无机磷(DIP)、有机磷(DOP)、碳生化需氧量(CBOD)、溶解氧(DO)耦合系统关系。由于 WASP中浮游植物的量是以浮游植物碳来表示, 因浮游植物碳在测量上较为困难, 实测数据少, 因此本研究以叶绿素 a(Chl-a)质量浓度代表浮游植物的量[9,15-16]。将PHYT,DON, NH4-N, NO3/NO2-N, DIP, DOP, CBOD, DO 8个水质指标的质量浓度分别以C1,C2,C3,C4,C5,C6,C7,C88个变量表示。四个模块之间的相互转换关系, 见图1(修改自WASP 6[3]), 模块中各变量的生成和消失项见表1。

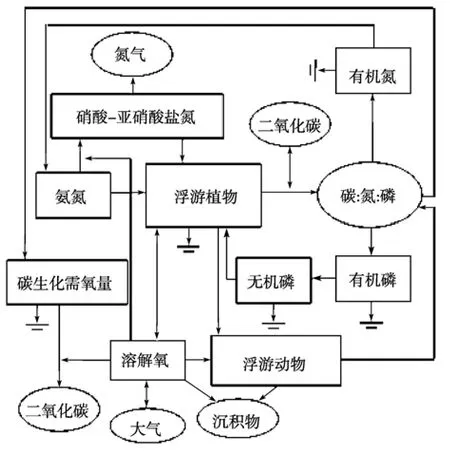
图1 围隔生态系水质模型系统关系图Fig. 1 Interaction of water quality modeling system in the mesocosm ecosystem

表1 模型变量消长因子Tab. 1 Increase and decrease factors of modeling variables

1.2 模型主要模块

1.2.1 浮游植物模块

浮游植物在系统动力循环过程中起着重要作用,它影响到水环境中氮、磷、溶解氧等状态变量。其主要反应动力学方程如公式(1)～(4)所示, 其他见WASP动力学公式部分[15]。

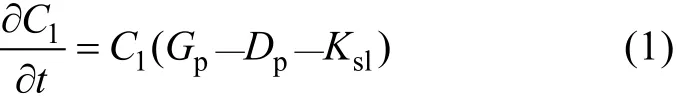
式中,Gp为浮游植物生长率(d-1),Dp为浮游植物呼吸与死亡率(d-1),Ks1为浮游植物沉降率(d-1)。

浮游植物生长率方程：

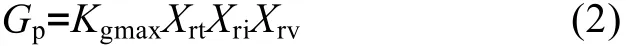
式中,Kgmax为 20℃时浮游植物最大生长率(d-1),Xrt为温度调节因子,Xri为光照限制因子,Xrv为营养盐限制因子。

浮游植物呼吸及死亡率方程：

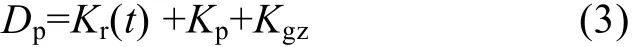
式中,Kr(t)为浮游植物内呼吸率(d-1),Kp为浮游植物代谢死亡率(d-1),Kgz为浮游植物被浮游动物摄食死亡率(d-1)。

浮游植物沉降率方程：

式中,Vs1为浮游植物沉降率(d-1),D为水深(m)。

1.2.2 磷循环模块

可溶解的或可利用的DIP通过吸附-解吸机理与颗粒无机磷相互作用。浮游植物由于生长而吸收DIP, 因此DIP合成了浮游植物生物量。通过内源呼吸和非吞食性死亡, 磷又从浮游植物生物体中返回到溶解和颗粒有机磷以及溶解无机磷。有机磷通过矿化能转化成溶解无机磷。其主要反应动力学方程如公式(5)～(6)所示：

有机磷：

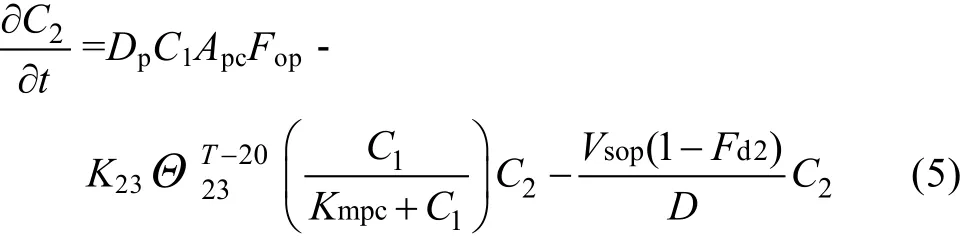
无机磷：

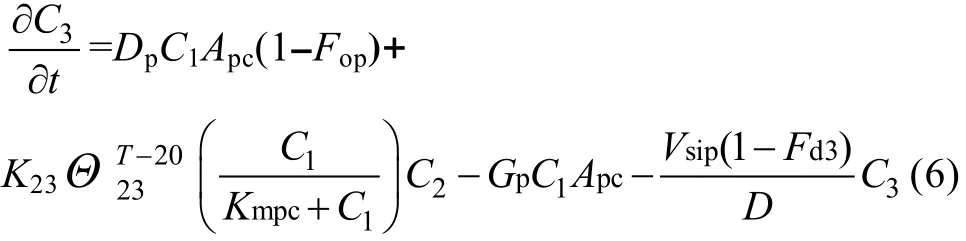
式中,Apc为浮游植物中磷碳比,Fop为浮游植物释放出磷中所含有机磷比例,K23为20℃时有机磷的矿化率(d-1), Θ23为K23的温度调整系数, Kmpc为矿化作用半饱和质量浓度(mg/L), Vsop为有机颗粒沉降速率(m/d), Fd2为有机磷中溶解态比例, Vsip为无机颗粒沉降速率(m/d), Fd3为无机磷中溶解态比例。

1.2.3 氮循环模块

浮游植物生长吸收氨氮和硝酸-亚硝酸盐, 并将其合成浮游植物生物量。吸收氮的速率是氮浓度的函数, 而其浓度又与总的可利用无机氮有关。通过内源呼吸和非吞食性死亡, 氮又从浮游植物生物量转化为溶解和颗粒有机氮以及氨。有机氮矿化为氨, 其矿化速率又依赖于温度, 而氨也可以转化成硝酸盐,其硝化速率也依赖于温度和氧气。硝酸盐在缺氧状况下, 也可以转化成氮气, 其反硝化速率是温度和氧气的函数。其反应动力学方程如公式(7)～(10)所示：有机氮：

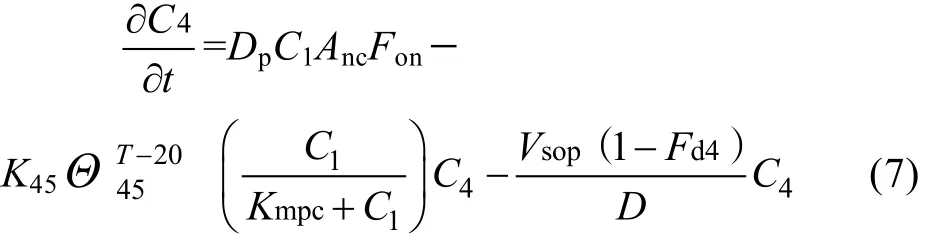
氨氮：

硝酸-亚硝酸盐氮：

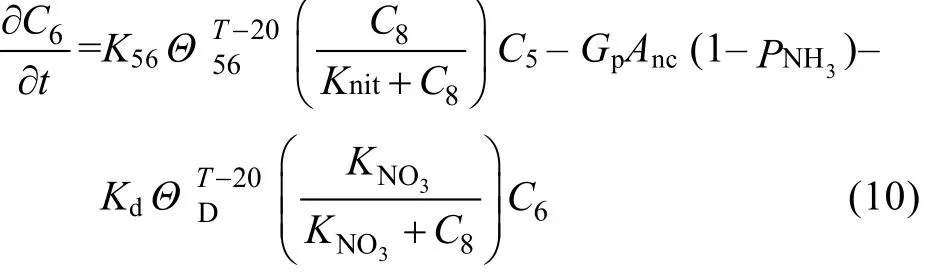
式中, Anc为浮游植物中氮碳比, Fon为浮游植物释放出氮中所含有机氮比例, K45为20℃时有机氮的矿化率(d-1), Θ45为K45的温度调整系数, Fd4为有机氮中溶解态比例, PNH3为浮游植物摄取氮营养盐中偏好氨氮程度, K56为20℃硝化速率(d-1), Θ56为温度调整系数, Knit为硝化作用半饱和质量浓度(mg/L),Kd为20℃时反硝化速率(d-1), ΘD为温度调整系数,为反硝化作用的半饱和质量浓度(mg/L)。

1.2.4 CBOD-DO子模块

溶解氧含量与其他状态变量相结合。溶解氧的来源有大气复氧和浮游植物的光和作用。溶解氧的消耗主要有浮游植物的呼吸作用、水体中碳质物质的氧化、硝化作用。其反应动力学方程如公式(11)～(12)所示：CBOD：

式中, Aoc为浮游植物中氧碳比, Kox为 20℃时CBOD氧化速率(d-1), oxΘ为温度调整系数, KBOD为CBOD半饱和质量浓度(mg/L), Fd7为CBOD中溶解比例, K2为20℃再曝气速率(d-1), 2Θ为温度校正系数, sC饱和溶解氧量(mg/L), O为 20℃时底泥耗氧量(g/m2), OΘ为温度调整系数。

1.3 模型计算方法

围隔生态系水质模型采用系统动力学DYNAMO(Dynamic Model, 动态模拟)语言[6]运行。模型包括一系列互相耦合的微分方程, 每一个连接库量(stock)和流量(flow)的方程式即是一个微分方程式。系统动力学中以有限差分方程式来表示, 再依时间步长对各方程进行求解, 求解过程为同步进行,并无时间先后差异, 呈现出系统在各时间点的同步变化状态。在stella9.0.2中, 提供了三种算法[14]对库量进行计算, 每种算法都有其优缺点, 本模型采用Runge-Kutta法, 其具有计算精度高, 稳定性好等优点[16]。在Δt的选择上, 小Δt虽能增加模拟的准确度,但增加了运算时间, 若 Δt取得太大, 则会使模拟结果失真, 故根据模拟的目的、模式的稳定性等因素确定本模型的时间步长为1 d。

2 计算结果与分析

围隔实验在象山港国华宁海电厂附近水域进行。共设三处围隔区M1, M2和M3, 本文选择了其中之一M3区围隔为例开展模型计算, M3区围隔站点位置为 121°32′19″E, 29°30′36″N。围隔采用漂浮式,底部无沉积物, 围隔袋采用透明聚乙烯薄膜, 围隔内置当地海水, 围隔装置见图2。

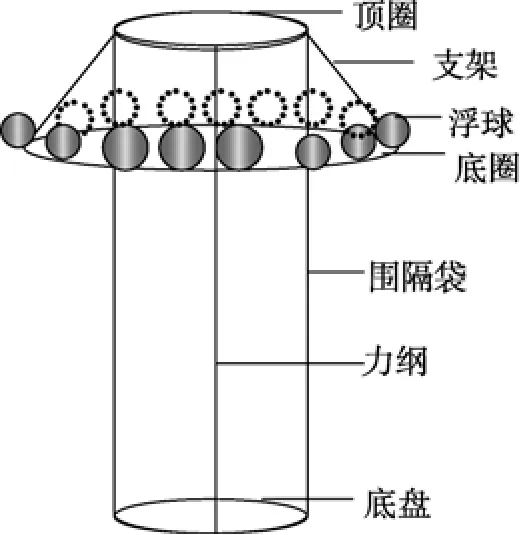
图2 围隔生态实验装置Fig. 2 Enclosure experimental configurations

2.1 验证资料说明

验证所用资料为2010年10月5～11日在围隔内监测的日平均水质和生物资料。监测项目包括了水温, 叶绿素 a, 溶解氧, 生化需氧量, 无机氮, 氨氮,硝酸盐氮, 亚硝酸盐, 总氮, 无机磷, 总磷, 浮游动、植物密度和生物量, 所有样品采集、处理均按《海洋监测规范》[17]进行。每天9：00和17：00各采一次样,采样深度0.5 m。生物样现场用5%甲醛溶液固定, 带回实验室鉴定、计数并称质量(湿质量)。实验期间,透过海面的太阳光合有效辐射强度平均为136.25 W/m2, 围隔袋内平均温度为25.63℃。

2.2 模型参数灵敏度分析及率定

2.2.1 参数灵敏度分析及率定方法

模型参数的可靠性对于模型模拟结果的合理性、准确性等起着重要的作用[18]。然而, 在模型中不可能对所有参数都进行实验室或现场测定, 因此,合理选择和确定模型参数是数值模型构建中至关重要的环节[19]。采用多参数灵敏度分析(MPSA)[20-22]的方法确定参数, 其步骤： (1)根据文献资料确定参数的取值范围; (2)在 Stella9.0.2软件灵敏度设置(sensitivity spec)菜单中, 对每一个系统的参数,在min和max中输入参数最小值和最大值, 并设置N个均匀分布的独立随机数; (3)应用生成的N个随机数运行模型, 计算相应的目标函数值; (4)将目标函数值与给定的指标R进行比较, 确定N个参数组中,哪些是“可以接受的”, 哪些是“不可接受的”; (5)评价参数灵敏度： 对每个参数, 比较“可接受的”与“不可接受的”两组参数值的分布情况, 绘制频数-累计频率曲线图, 如果两种分布形式相同, 则表明该参数不敏感, 反之, 则该参数较敏感。两条累积频率曲线分离程度代表了参数的灵敏度。目标函数值采用模拟值与参数取值范围的中值的模拟值的误差平方和表示。指标R值为三种不同目标函数值, 即模拟N个目标函数值排序后的33%, 50%和66%。

2.2.2 参数灵敏度分析及率定结果

围隔生态系水质模型涉及 4个子系统, 涉及参数多达 30个, 本文仅以浮游植物系统为例, 对其涉及的需要优化的7个参数(表2)进行多参数灵敏度分析。其他模块参数直接给出灵敏度分析后的结果, 见表3。模型运行次数N=100, 指标R取值在目标函数值排序位置 50分点处。MPSA统计结果见图 3, 两条曲线分离的程度越大, 表示该参数的灵敏度越大。通过计算图3中每个参数的两条曲线的分离程度SD(采用与Nash-Sutcliffe效率系数[23]), SD值越接近1,表明参数越不灵敏。由此得到, 7个参数的灵敏度从大到小依次是：Krc,Kpc,Kgmax,Is,Ia,Ke,Kg。SD值见表2, 即20℃浮游植物内呼吸率, 20℃浮游植物代谢死亡率, 20℃时浮游植物最大生长率是重要的参数;浮游植物生长最适光强度, 水表面白天平均日照强度是比较重要的参数; 光衰减系数和浮游动物摄食率则在模拟过程不会造成显著的影响。

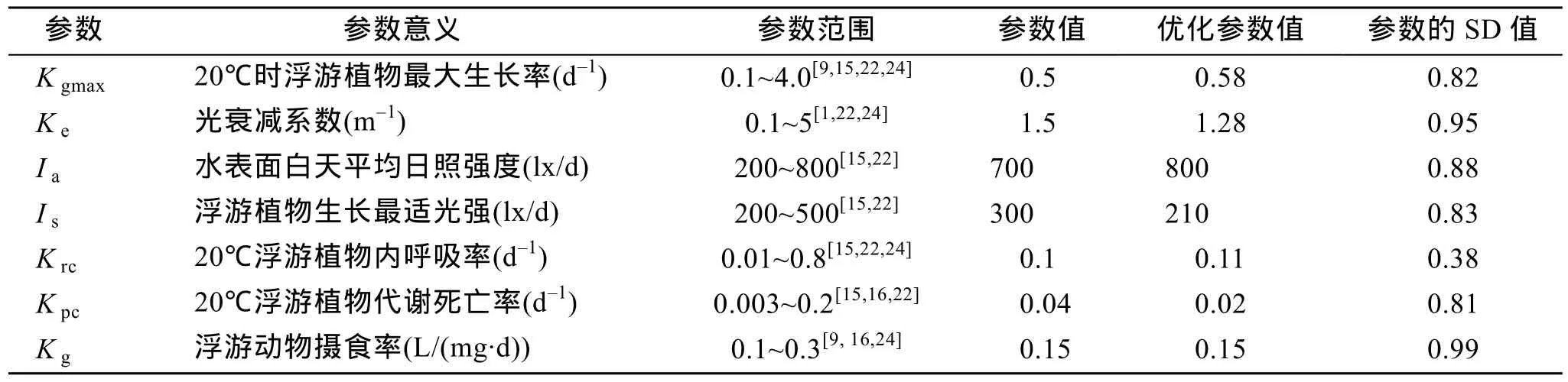
表2 浮游植物模块参数设定Tab. 2 The model parameters settings of Phytoplankton

由图 3中的可接受频数柱状图可以看出, 最高可接受频数对应的参数值可初步设为参数值, 即Krc≈0.1(频数 17)、Kpc≈0.04(频数 17)、Kgmax≈0.5(频数17)、Is≈300(频数 13)、Ia≈700(频数 13),Ke≈1.5(频数13),Kg≈0.15(频数20)。在初步定出参数值后, 利用软件中滑块(Slider input device)和旋钮(Knob input device)输入器, 对照M2、M3区围隔实验的Chl-a部分实测值进行优化参数, 最终得到浮游植物模块主要参数值, 见表2。

2.2.3 初始值设定

以M3区围隔内第1天监测的8个指标作为水质模型各状态变量的初始值。由于藻类呼吸作用和藻类碳衰减的影响, 测量的BOD5数据不能和模型计算的内部 CBOD 结果直接进行比较[3,22], 因此, 须对BOD5进行校正。综上, 各模块变量初始值设定见表4。

2.2.4 其他设定

将围隔内水温T(t)和浮游动物Z(t)随时间(d)变化作为重要影响因素带入 stella9.0.2转化器(Converter)图形功能(Graphical Function)中模拟。DON, NH4-N, NO3/NO2-N以总氮(TN)形式输出。DIP,DOP以总磷(TP)形式输出。

表3 其他模块参数设定Tab. 3 The model parameters settings of others modules

表4 变量初始值设定Tab. 4 The initial value settings of module variables

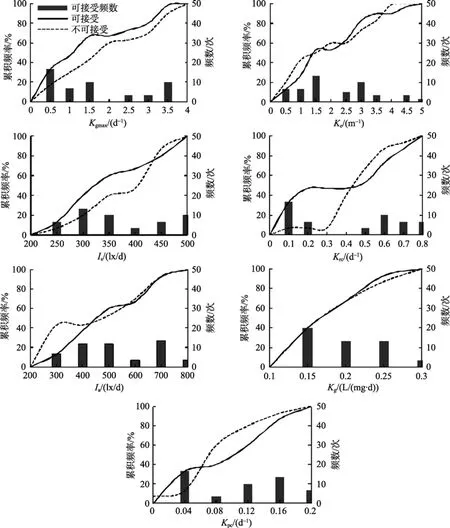
图3 多参数灵敏度分析Fig. 3 Multi-parameter sensitivity analysis

2.3 模型验证

用实测资料对模型进行了验证, 见图4。结果表明, 模拟计算的 Chl-a质量浓度的平均值为 2.128×10-3mg/L, 实测质量浓度平均值为 1.873×10-3mg/L,相关系数(R)为 0.851, 为显著相关; DO质量浓度模拟均值为3.004 mg/L, 实测平均值为4.557 mg/L,R为0.907, 为高度相关; 其他水质指标TP, TN, CBOD的模拟结果与实验结果基本吻合。见表5。

模拟结果进一步表明, 该模型基本能反映象山港围隔生态水质各状态变量的变化, 浮游植物叶绿素a的质量浓度呈上升趋势, 与总磷、总氮等的质量浓度变化大致相反, 这是由于浮游植物生长大量摄取营养盐。溶解氧作为关键的水质指标, 与碳生化需氧量变化趋势大致相同, 与浮游植物趋势却相反,由于浮游动物的摄食, 浮游植物受捕食死亡率增加,使得浮游植物增长不明显, 见图 4, 进而使得溶解氧生产不明显, 另一方面, 由于浮游植物、浮游动物的

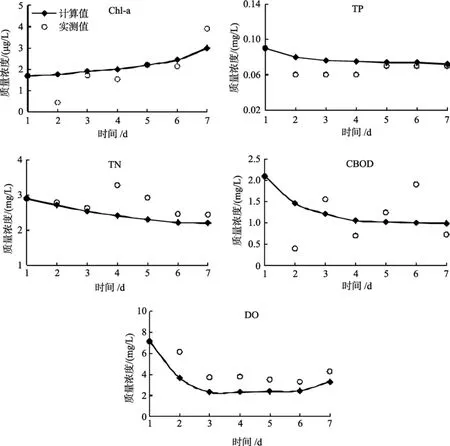
图4 象山港海洋围隔生态实验结果与模拟结果比较Fig. 4 Comparison of enclosure experimental observational data and simulated result

表5 M3区围隔生态系各水质指标的模拟值与实测值Tab. 5 The simulated and measured values of water quality indices in M3 Enclosure

呼吸作用、硝化作用和碳生化需氧量耗氧明显, 使得溶解氧整体趋势下降。在实测结果中可能由于偶然性外界因素的影响, 如光照、降雨等, 模拟结果不能完全体现生态水质各指标质量浓度随时间剧烈变化,但能反映出其变化的总体趋势。

2.4 讨论

本研究利用系统动力学软件建立的围隔生态系水质模型的图形界面易于了解和修改, 应用方面有更广阔的空间。另外, 本模型为一维箱式模型, 未涉及表、底层水质的不同对结果的影响, 后继研究中可以利用Stella9.0.2软件具有的阵列(Array)选项, 模拟二维方向上水质变化, 解决一般系统动力学模型较难表达空间变化的问题。在本次模拟中, 浮游动物Z(t)仅以实测变量带入转化器(Converter)中。后继研究中可以将其以库量形式列入, 但需要考虑浮游动物呼吸及死亡对有机磷模块、有机氮模块、CBOD模块生成项(见表1)的贡献, 此将革新整个WASP模型, 使得预测结果更符合实际情况。

3 结论

本文以WASP中的EUTRO概念模式, 加入了水温和浮游动物在水质生化反应过程中所起的作用,根据围隔实验的实际情况, 全面分析各影响因素,采用系统动力学方法建立生态水质模型, 模型包括浮游植物、溶解氧、总氮、总磷、碳生化需氧量和浮游动物变量, 以及30余个主要生态水质动力学参数。通过所建立的围隔水质动力学模型, 模拟了2010年秋季不同温度条件下围隔生态水质生化过程, 并利用2010年秋季海洋围隔生态实验数据对模型进行了验证。模拟结果与实际变化基本吻合, 说明模型逻辑结构及其相关动力学方程基本合理, 运用多参数灵敏度分析法(MPSA)所确定的模型参数能够反映象山港海域的地域化特征, 本模型为揭示象山港浮游生态系统生态水质动力学机制提供了科学基础。

[1] United States Environmental Protection Agency(USEPA). River and stream water quality model(QUAL2K) [EB/OL]. [2011-03-15]. http：//www.epa.gov/athens/wwqtsc/html/qual2k.html.

[2] Danish Hydraulics Institute. MIKE21： User guide and reference manual [EB/OL]. [2011-03-15]. http：//www.mikebydhi.com/Download/MIKEByDHI2011.aspx.

[3] United States Environmental Protection Agency(USEPA). Water quality analysis simulation program(WASP) [EB/OL]. [2011-03-15]. http：//www.epa.gov/athens/wwqtsc/html/wasp.html.

[4] 陈美丹, 姚琪, 徐爱兰. WASP水质模型及其研究进展[J]. 水利科技与经济, 2006, 12(7)： 421-422.

[5] Forrester J W. Industrial dynamics [M]. Cambridge,MA： MIT Press, 1961： 56-70.

[6] Ford A, 唐海萍, 史培军. 环境模拟： 环境系统动力学模型导论[M]. 北京： 科学出版社, 2009： 15-18.

[7] Richmond B M. An introduction to systems thinking[M]. Lebanon： Isee systems Inc, 2004： 3-44.

[8] 崑陆贤. 海洋围隔生态系实验在海洋污染控制中的应用[J]. 环境科学, 1987, 8(4)： 78-83.

[9] Grice G D, Reeve M R. Marine mesocosm： Biological and chemical research in experimental ecosystems[M].New York： Springer Verlag, 1982： 1- 430.

[10] Baretta-Bekker J G, Riemann B, Baretta J W, et al. Testing the microbial loop concept by comparing mesocosm data with results from a dynamical simulation model[J]. Marine Ecology Progress Series, 1994, 106： 187-198.

[11] Baretta-Bekker J G, Baretta J W, Hansen A S, et al. An improved model of carbon and nutrient dynamics in the microbial food web in marine enclosures[J]. Aquatic Microbial Ecology, 1998, 14： 91-108.

[12] Beyers R J, Odum H T. Ecological microcosms [M].New York： Springer Verlag, 1993： 1-557.

[13] Costanza R, Gottlied S. Modeling economical and economic systems with STELLA： Part [J].Ⅱ Ecol Model, 1998, 112(2)： 81-84.

[14] Isee systems, inc. Systems thinking software[EB/OL].[2011-03-15]. http：//www.iseesystems.com/.

[15] 陈函馨. 以系统动力学建立感潮河川水理与水质模式[D]. 中国台湾： 国立中山大学, 2002.

[16] 王旭东, 刘素玲, 张树深, 等. 白洋淀水域 WASP富营养化模型改进研究[J]. 环境科学与技术, 2009,32(10)： 22-23.

[17] GB 17378-2007《海洋监测规范》[S].

[18] 高会旺, 孙文心, 翟雪梅. 水层生态系统动力学模型参数的灵敏度分析[J]. 青岛海洋大学学报, 1999,29(3)： 398-404.

[19] Harmon R, Challenor P A. Markov chain monte carlo method for estimation and assimilation into models[J].Ecological Modeling, 1997, 101(1)： 41-59.

[20] Mao Jingqiao, Chen Qiuwen, Chen Yongcan.Three-dimensional eutrophication model and application to Taihu Lake, China [J]. Journal of Environmental Sciences, 2008, 20： 278-284.

[21] 王纲胜, 夏军, 陈军锋, 等. 模型多参数灵敏度与不确定性分析[J]. 地理研究, 2010, 29(2)： 263-269.

[22] 郭丽君. 水科学研究： 水质分析模拟程序6 (WASP6)专题 [J/OL]. [2011-03-15]. http：//www. waterscience.cn/journal/index.html.

[23] Choi J, Harvey J W, Conklin M. Use of multi-parameter sensitivity analysis to determine relative importance of factors influencing natural attenuation of mining contaminants [J/OL]. [2011-03-15]. http：//toxics.usgs.gov/pubs/wri99-4018/Volume1/sectionC/1405_Choi/index.html.

[24] 李克强, 王修林, 韩秀荣, 等. 胶州湾围隔浮游生态系统氮、磷营养盐迁移-转化模型研究[J]. 海洋学报,2007, 29(5)： 76-81.

Study on the water quality model of the mesocosm ecosystem in the Xiangshan Bay

YANG Hong, DING Jun, WANG Chun-feng, CHEN Jian, LIU Cheng-xiu,DAI Gui-xiang, ZHAO Ying
(Marine Sciences College, Shanghai Ocean University, Shanghai, 201306, China)

Mar.,25,2011

the Xiangshan Bay; system dynamics; the water quality analysis simulation program (WASP); water quality dynamic model; mesocosm ecosystem

Based on the conceptions of the water quality analysis simulation program (WASP) developed by United States Environmental Protection Agency (USEPA), a water quality dynamic model of ocean mesocosm ecosystem was established using system dynamic software-Stella9.0.2. The model consists of four modules： Phytoplankton,Phosphorus Cycle, Nitrogen Cycle and Carbonaceous Biochemical Oxygen Demand-Dissolved Oxygen Cycle, and eight variables including Chlorophyll a, Organic phosphorus, Inorganic phosphorus, Organic nitrogen, Ammonia,Nitrate-Nitrite nitrogen, Biochemical oxygen demand and Dissolved oxygen were involved in it. The results showed that this model could simulate the water quality variations properly in mesocosm ecosystem under different water temperature conditions, based on the site experiment data in the Xiangshan Bay in early October, 2010. Not only the logical structure but also the model parameters were feasible, and more than 30 parameters were made during the simulation. In short, the model demonstrated the advantages of the system dynamic simulation and provide scientific evidence for revealing dynamic mechanism, simulating and predicting changes of the marine ecosystems in the Xiangshan Bay.

P731.26

A

1000-3096(2012)07-0014-09

2011-03-25;

2012-04-27

科技部海洋公益性行业科研专项资金项目(200905010-10)作者简介： 杨红(1962-), 女, 江苏无锡人, 教授, 主要从事环境监测、环境评价及环境管理研究, 电话： 021-61900335, E-mail： hyang@shou.edu.cn

(本文编辑：刘珊珊)