三分量应变传感器弹性体结构设计*

于常安，李 平，王 罗

(1.重庆大学光电工程学院，教育部光电技术及系统重点实验室，重庆 400030；2.中国空气动力研究与发展中心设备设计与测试技术研究所，四川绵阳 621000)

为了满足现代战争的需要，新型军用飞机不仅需要具有高空高速性能，而且要具有机动、敏捷和隐身等方面的性能。理论和实践证明，推力矢量技术使飞机具有了过失速超机动性、高敏捷性、短距起降性能、隐身性能和超声速巡航能力、该技术的应用大大提高了战斗机的作战效能和生存能力。西方国家早在20世纪60～70年代就开始研究推力矢量技术，目前已转入工程发展阶段，如美国的F－22、俄罗斯的苏－37 等飞机都已安装了推力矢量喷管［1－3］。矢量推力的独特优势，也逐渐在战术导弹中得到了应用，并展开了广泛的研究［4－7］。推力矢量技术的基础是推力矢量喷管技术，推力矢量喷管是指可用于飞行姿态控制(如俯仰、偏航、滚转和反推力等)的多功能排气喷管，优先发展轴对称矢量喷管发动机已是国际航空界的共识［8－10］。因此，研制一种用于测量推力矢量喷管性能实验的六分量测力系统，以对推力矢量进行精确的测量，就显得尤为重要。

六分量测力系统的核心部件是六分量天平，由于矢量喷管是内流式的，传统的内式天平没有安装空间，只能采用外式天平。常用的六分量外式天平主要有机械天平和六分量盒式天平，以往的矢量喷管六分量测量平台多采用机械天平［11］，机械天平虽然测量精度高、稳定性好，但是传感器之间分散独立、结构复杂、设计加困难、安装调试周期长、使用维护繁琐，近年来，随着应变天平技术的不断进步，机械天平已逐步被盒式应变天平取代。盒式应变天平是测力天平的一种，其刚度大，力与力矩机械分解比较彻底，因而干扰量小，测量精度高。盒式天平有整体式与装配式之分，整体式盒式天平加工要求高，一般尺寸较小，无法满足矢量喷管测力要求。而装配式盒式天平采用装配式结构，由固定框、浮动框和四个三分量应变传感器组成(图1)，装配后实现六分量力与力矩的测量，有易加工、承载能力高、刚度大、精度高、稳定性好等特点，可以满足矢量喷管六分量测力需要。其中三分量应变传感器是装配式盒式天平的核心，直接关系到六分量盒式天平的测量性能，针对装配式盒式天平要求，本文介绍了一种新型三分量力学传感器弹性体的结构设计，与以往的传感器相比，结构新颖，刚度大，精度高，适合装配式天平使用，另外抗弯能力强，可作为传感器独立使用。

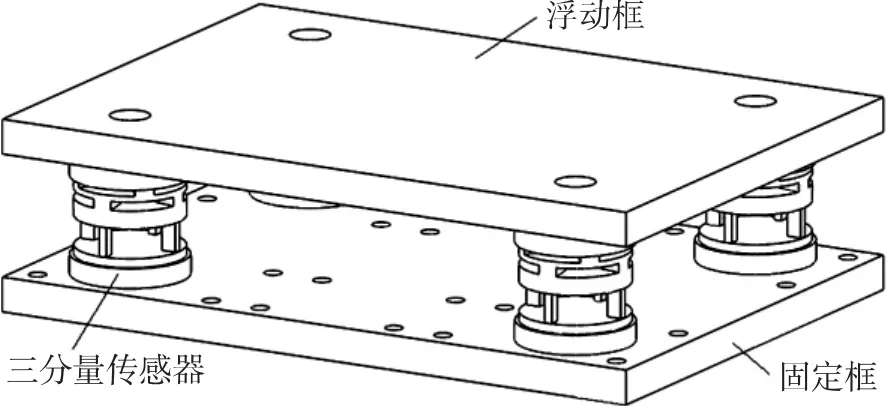
图1 盒式天平示意图

1 工作原理

应变式多分量力学传感器由弹性元件、应变计与测量电路(测量电桥)组成。测力实验时，弹性元件在载荷作用下产生变形，其应变与外力大小成正比。粘贴在弹性元件表面的应变计也同时产生变形，使其电阻值发生变化，有一个增量。这个电阻增量由应变计组成的惠斯通全桥测量电路把它转换成电压增量，该电压增量值与应变天平所承受的载荷值成正比。将电压信号通过A/D装换后，输入到计算机上进行处理，即可得到作用在模型上的空气动力与力矩。

多分量传感器通过不同的结构形式的测量元件，力求使它们在载荷的作用下，对各自预测量分量的载荷敏感，产生相对明显的变形，而对其它分量载荷不敏感，不产生或产生尽量小的变形，实现结构上对力与力矩的机械分解或部分机械分解。另外，再通过应变计的粘贴位置与全桥测量电路的设置，使其它分量载荷所产生的应变不改变电桥的平衡状态，实现力与力矩的电气分解［11］。

2 设计载荷

根据六分量盒式天平载荷要求，分配到三分量传感器载荷如下:

推力Fx=4 900 N

升力Fy=±7 840 N

侧力Fz=±3 920 N

3 弹性体结构设计

设计传感器弹性体时，一般要考虑两个重要参数，一是传感器的应变值，应变值越大，产生的应变信号值就越大，灵敏度就越高；二是传感器的刚度，刚度越大，位移量越小，稳定性就越好。为获得较高的应变值和较大的刚度，弹性体的结构布局和材料的选取就显得尤为关键了。根据三分量力传感器载荷量程特点及天平总体布局、尺寸要求等因素，三分量力传感器的测量单元的结构设计形式为串、并联组合结构(图2)，推力和侧力单元并联，然后与升力单元串联。

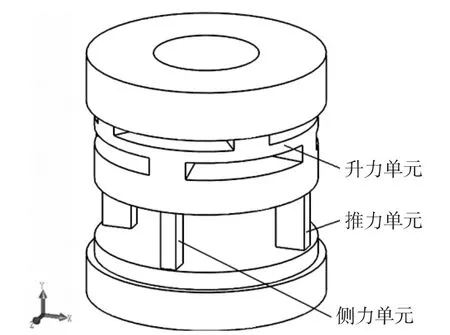
图2 三分量传感器示意图

3.1 弹性体材料

为保证传感器的测量精度和稳定性，弹性体材料要具有良好的弹性、较高的强度、较高的冲击韧性和疲劳强度、有较小的线膨胀系数、有良好的弹性模量随温度变化的稳定性以及有良好的机械加工性能与热处理工艺性能［12］。

根据以上要求，结合以往设计经验，弹性体材料选择马氏体时效钢(00Ni18Co8Mo5TiAl)，该材料物理参数如下:

弹性模量E=1.872 5×1011N/m2

剪切弹性模量G=6.664×1010N/m2

强度极限 σb=1.862×109N/m2

泊松比 μ=0.29

屈服极限 σs=1.754×109N/m2

由此可见，马氏体时效钢(00Ni18Co8Mo5TiAl)是理想的传感器弹性体材料。

3.2 推力与侧力单元的设计

推力单元和侧力单元采用四柱梁式组合单元并联构成，通过不同的组桥方式实现推力、侧力的测量(图3)。上下两个梁柱与左右两个梁柱对称设置，分别作为推力和侧力的测量弹性单元，四个梁柱的长度相同。

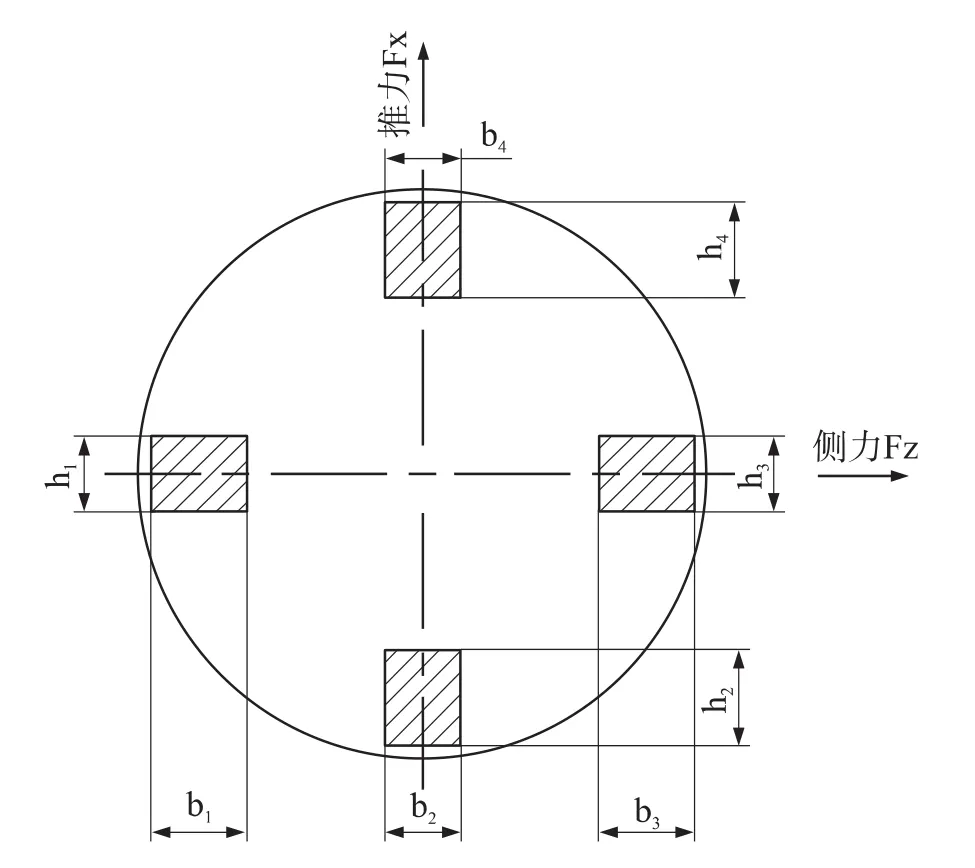
图3 四梁柱组合元件示意图

如图3所示，用梁柱2、4测量推力Fx，在推力作用下，作用在弹性体元件上的最大弯矩Mmax为

式中L为前后组合单元梁之间的距离。这时，梁柱2、4产生单弯曲变形。根据载荷按刚度分配原则，梁柱2所承受的力矩M2为［12］

其中，b1、h1分别为梁柱1截面宽度与高度，b2、h2分别为梁柱2截面宽度与高度。梁柱2的最大应力σmax为［12］

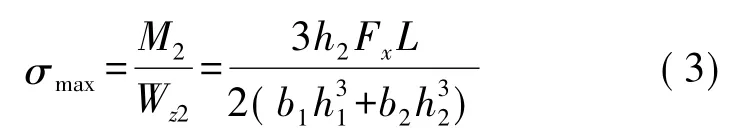
因此，梁柱2的最大应变为［12］

同理，用梁柱1、3测量侧力Fz，得出最大应力为［12］

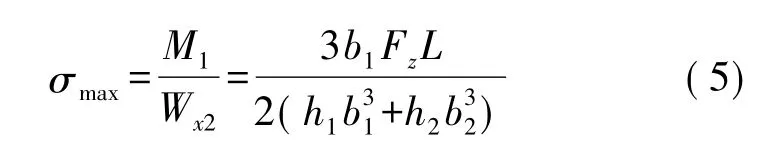
梁柱2的最大应变为［12］

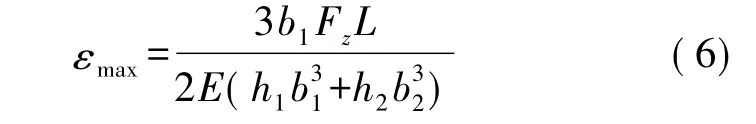
3.3 升力单元的应变设计

升力单元设计为环式弹性元件(图2)，在弹性体筒壁上设计四个支撑柱，四个加载柱，上下分布，交叉45°，对应成两端固定、跨中受载的应变梁，在升力作用下，该应变梁可简化成矩形超静定梁，即整个升力测量单元由8个超静定梁组成。根据超静定梁定义，在受到集中载荷是，超静定梁的自由端的端部只有移动，没有转动，即产生S形变形(图4)。

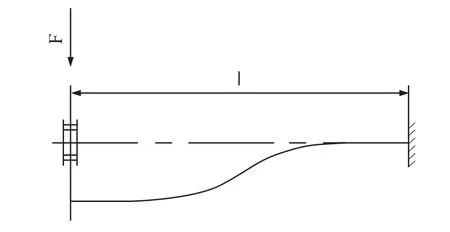
图4 超静定梁S形变形

测量单元的最大应力为［13］

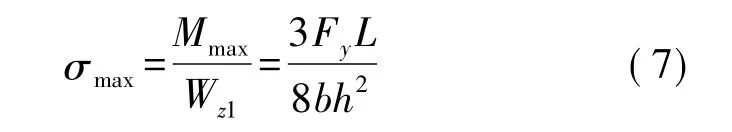
测量单元上最大应变为

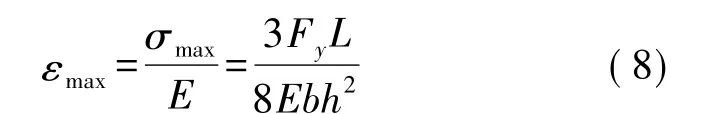
根据以上公式可以计算出各测量单元的应变分别为:推力:470.5×10－6；升力:240.6×10－6；侧力:475×10－6。

通过计算，调整推力和侧力组合单元梁柱的宽度和厚度，使两个测量单元的应变值在载荷不同的情况下趋于一致，保证传感器的平衡性。升力单元的应变值设计偏低，主要是考虑到由于由传感器组成的六分量天平上方还要承载测力系统的其他部件，设计上留有余量。

4 有限元分析

有限元方法是20世纪60年代发展起来的一门数值技术，随着电子计算机的发展，它在工程上得到了广泛的应用。近些年来已成为风洞天平和各种应变传感器的主要设计手段之一［15－19］。

通过计算确定应变量尺寸后，对三分量传感器进行建模，采用大型有限元分析软件MSC对模型进行仿真，对传感器三个受力工况进行有限元计算。

由于传感器弹性体结构形式特殊，划分网格是采用的是10节点的四面体单元(图)，模型节点数75 894，单元数 49 640。

工况一，Fx=4 900 N，应变云图见图5，所得贴片处平均应变为 450×10－6。

工况二，Fy=7 840 N，应变云图见图6，所得贴片处平均应变为 194×10－6。

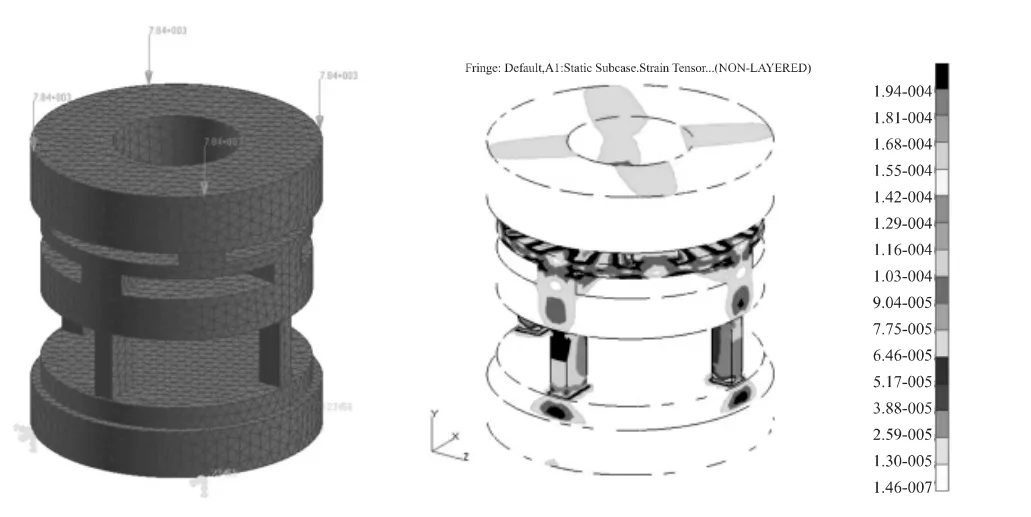
图6 升力工况与满载荷应变云图

工况三，Fz=3 920 N，应变云图见图7，所得贴片处平均应变为 466×10－6。

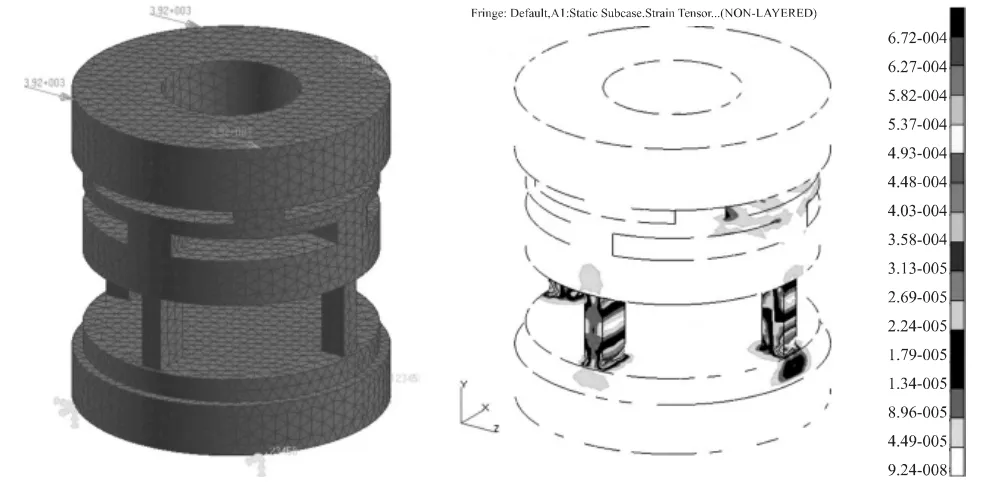
图7 侧力工况与满载荷应变云图

通过MSC软件工况设置，有效模拟了传感器实际工作状态，直观的反映出传感器在受力情况下的应变分布。从应变云图上看，传感器刚度分配合理，力分解彻底。

5 试验及讨论

弹性体加工完成后，经过热处理、打磨、贴片、组桥、温度补偿和灵敏度补偿等一系列工艺处理，三分量力传感器进入校准阶段(图8)，校准数据所得信号经过换算，得出传感器的测量应变值数据与理论应变值如表1所示。

表1 应变数据对比

图8 三分量传感器校准

从表1中可得以下几点:①四只传感器测量应变值基本一致，略有差异；②理论应计算变值大于实测平均应变值；③有限元计算应变值与实测应变值接近。

具体原因如下:①传感器受工艺的影响(如加工尺寸、贴片位置等引起的偏差)，会出现传感器与传感器之间，传感器实测值与理论值之间出现差异；②理论应计算的出的结果是应变梁的最大应变值，而应变片有一定的面积，所受的是应变片贴片位置的平均应变值；③有限元可以反应出测力单元应变梁受力时的平均应变值，更好的反应弹性体的工作状态。

理论计算应变、有限元计算应变、实际测量应变数值上大体一致，略有差异，且差异完全处于可以接受的范围之内。由此可见，这种新型三分量力传感器弹性体所采用的串并联联合结构的布局和测量单元应变梁尺寸是正确的，完全达到了预期要求，可以作为装配式盒式天平的测量元件，弹性体设计是成功的。另外，有限元计算可有效模拟传感器弹性体的工作状态，可用于弹性体的设计计算或验证，确定应变片粘贴位置，减少测量误差。

6 结论

三分量传感器设计采用了传统的材料力学计算和有限元分析相结合的方法，对弹性体进行设计计算，取得了较好的效果。盒式天平经组装后，进行了单分量加载校准及综合精度加载，结果表明:各分量加载精准度指标达到或超过预期指标要求，天平机械滞后小、重复性高，整体刚度大。天平目前已用于某型航空发动机矢量喷管六分量测力试验，性能稳定。

［1］陶增元，李军，程邦勤.飞机推进系统关键技术—推力矢量技术［J］.空军工程大学学报，2000，1(2):87－90.

［2］Kowal H J.Advances in Thrust Vectoring and the Application of Flow-Control Technology［J］.Canadian Aeronautics and Space Journal，2002，48(2):145－151.

［3］周慧晨，谭慧俊，孙姝，等.一种矢量增强型双喉道射流推力矢量喷管的数值模拟［J］.航空动力学报，2000，25(9):2070－2076.

［4］李泽勇.一种冲压发动机推力矢量设计方案研究［J］.固体火箭技术，2008，31(3):228－231.

［5］王鹏，陈万春，殷兴良.空空导弹大角度姿态推力矢量控制研究［J］.宇航学报，2004，25(3):295－299.

［6］王青，景韶光，张明廉.推力矢量空空导弹的变结构自适应控制［J］.航空学报，2000，21(4):352－354.

［7］DrErland rbekk.Supersonic Split Line TVC Technology and Testing at Nammo Raufoss As［R］.AIAA 2006－4940.

［8］靳宝林，朱明俊.航空发动机推力矢量技术发展趋势［J］.航空发动机，1997(1):44－49.

［9］李晓明，伏宇.轴对称矢量喷管机构优化设计［J］.燃气涡轮试验与研究，2006，19(3):1－4.

［10］Kowal H J.Advances in Thrust Vectoring and the Application of Flow-Control Technology［J］.Canadian Aeronautics and Space Journal，2002，48(2):145－151.

［11］付尧明，王强，额日其太，等.矢量喷管六分量测力试验台的研制［J］.流体力学实验与测量，2002，16(1):87－93.

［12］贺德馨.风洞天平［M］.国防工业出版社，1999:67－68，178－179，121－122.

［13］刘鸿温.材料力学［M］.高等教育出版社，1995:123－124.

［14］秦岗，曹效英，宋爱国，等.新型四维腕力传感器弹性体的有限元分析［J］.传感技术学报，2003，16(3):238－241.

［15］杨中艳，解亚军.六分量盒式应变天平的有限元分析［J］.弹箭与制导学报，2010，30(2):201－204.

［16］冯志刚，王祁，信太克规.自确认压力传感器结构参数设计及其有限元分析［J］.传感技术学报，2007，20(2):279－282.

［17］姚裕，张召明.整体式盒式应变天平有限元设计［J］.南京航空航天大学学报，2010，42(1):58－61.

［18］刘九卿.整体三柱、四柱型称重传感器的力学特性分析［J］.衡器，2009，(1):3－5.

［19］易伟，陈世超，徐尹杰.整体四柱式力传感器弹性体的有限元分析［J］.中国测试，2011，30(2):89－92.