一种基于双谱的信号检测方法

杨 政，杨春武，王明洲

(1.中国船舶重工集团公司第七〇五研究所，陕西 西安 710075;2.水下信息与控制重点实验室，陕西 西安 710075)

0 引言

所谓微弱信号［1］的检测，就是通过一定方法抑制噪声，恢复、提取有用信号，提高信噪比。传统的微弱信号检测理论和方法采用似然比检测，但其有2个明显的缺点:①要求观测对象必须满足高斯条件的假设;②当观测噪声的信噪比下降时，系统的检测性能急剧下降，很难得到满意的检测概率。现代数字信号处理的发展，带动着各种新的理论和方法不断出现。其中高阶谱分析是在相关函数、功率谱理论等二阶统计量的基础上发展起来的［2］，具有以下优点:①能抑制高斯噪声，从而能提高参数估计性能;② 包含了相位信息，可用于非最小相位系统和信号的辨识;③能反映随机过程的分布偏离高斯分布的程度，可用于信号分类;④ 能检测刻画信号的非线性特性或者辨识非线性特性［3］。

本文利用双谱对叠加高斯噪声的信号进行检测，经仿真结果比较，在低信噪比的情况下，基于双谱的信号检测方法比传统的FFT方法检测效果更好。

1 随机变量的特征函数

假设随机变量x的概率密度函数为p(x)，它的特征函数定义为:

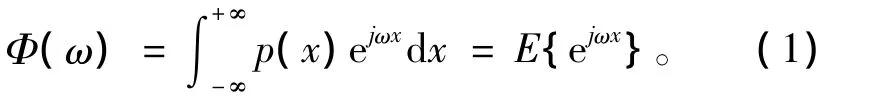
对式(1)取对数，得到随机变量x的第二特征函数

推广至k维随机矢量x=［x1x2…xk］T的特征函数定义为:

其中:ω =［ω1ω2…ωk］T。相应的，随机矢量x的第二特征函数定义为:

2 随机变量的矩、累积量

对随机矢量x=［x1x2…xk］T的特征函数Φ(ω)作r=v1+v2+… +vk阶偏导数，

取ω1=ω2=… =ωk=0，式(5)变为:

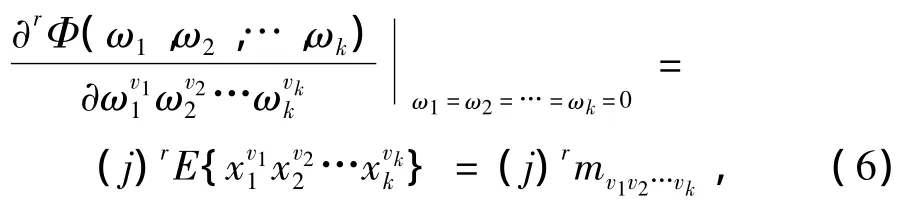
即随机矢量x=［x1x2…xk］T的r=v1+v2+… +vk阶矩为:

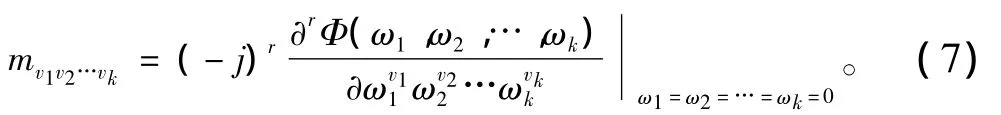
同理，对随机矢量x=［x1x2…xk］T的第二特征函数Ψ(ω)作r=v1+v2+…+vk阶偏导数，并取ω1= ω2=… =ωk=0，可得随机矢量x=［x1x2…xk］T的r=v1+v2+… +vk阶累积量为:

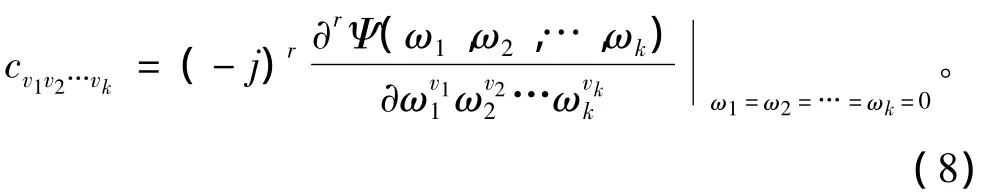
特别的，取v1=v2=… =vk=1，得到最常见的k阶矩和k阶累积量，分别记作

和

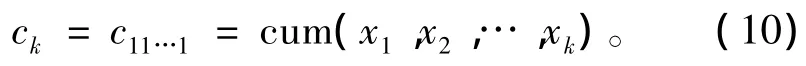
3 随机过程的矩、累积量

设{x(t)}是k阶平稳随机过程，则该随机过程的 k 阶矩 mkx(τ1，τ2，…，τk－1)定义为

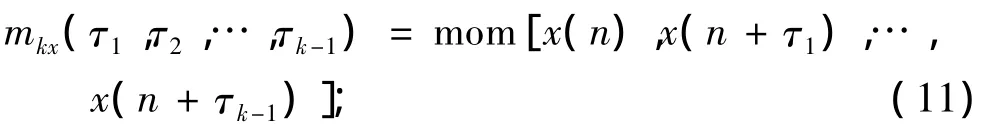
k 阶累积量 ckx(τ1，τ2，…，τk－1)定义为:

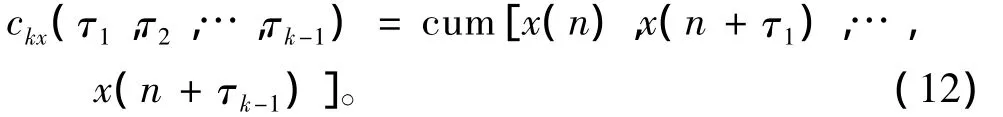
比较式(9)和式(12)可知，平稳随机过程的k阶矩和k阶累积量实际上就是随机矢量

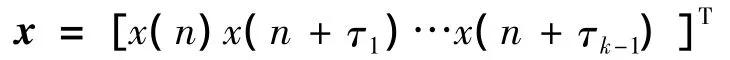
的k阶矩和k阶累积量。

4 高阶谱

随机过程的功率谱定义为自相关函数的Fourier变换。类似的，随机过程{x(n)}的高阶矩谱和高阶累积量谱分别定义为高阶矩和高阶累积量的Fourier变换。

设高阶矩 mkx(τ1，τ2，…，τk－1)绝对可和，即

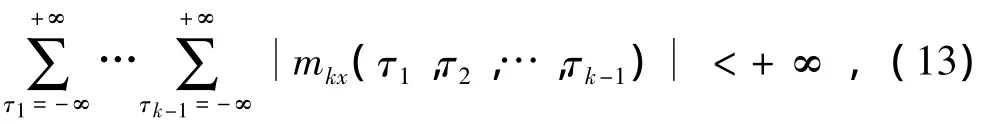
则k阶矩谱定义为:

设高阶累积量 ckx(τ1，τ2，…，τk－1)绝对可和，即

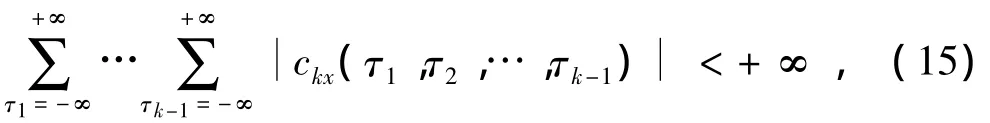
则k阶累积量谱定义为:

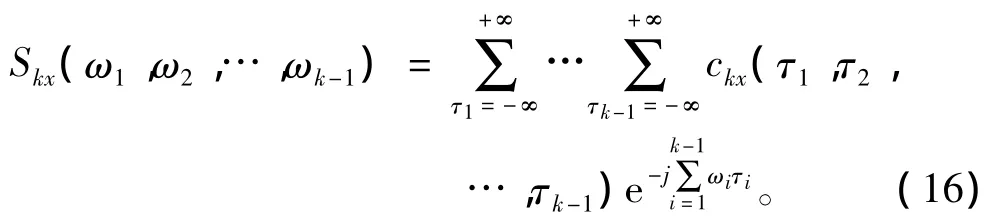
高阶矩、高阶累积量及其相应的谱是4种主要的高阶统计量。通常高阶累积量谱简称高阶谱或多谱。

常用的高阶谱有三阶谱和四阶谱，即

通常称三阶谱为双谱，四阶谱为三谱。

在实际的信号处理中，高阶累积量和高阶矩各有特点，一般高阶矩及其谱适合确定性信号的瞬态特性或周期性的分析，而高阶累积量及其谱适合随机信号的处理，主要原因有:高阶累积量能抑制高斯噪声，同时统计独立随机过程之和的累积量等于各自累积量之和，而高阶矩没有这些特点。因此，高阶累积量及其谱在非高斯随机过程中得到了广泛应用［4］。

5 基于双谱的信号检测

信号的检测问题就是判断观测数据中是否有目标信号存在［5］。检测系统的输入(即观测数据)x(k)有2种可能，即x(k)=s(k)+n(k)或x(k)=n(k)，其中，k=1，2，…，N，s(k)和 n(k)分别为信号和干扰，检测系统的任务就是对输入x(k)进行运算或处理，然后对检测额输出进行判断是否有信号存在。一般情况下，信号s(k)和噪声n(k)之间相互独立。

基于传统的功率谱估计方法，则有

基于双谱方法，则有

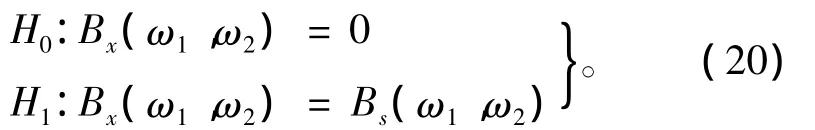
6 仿真验证

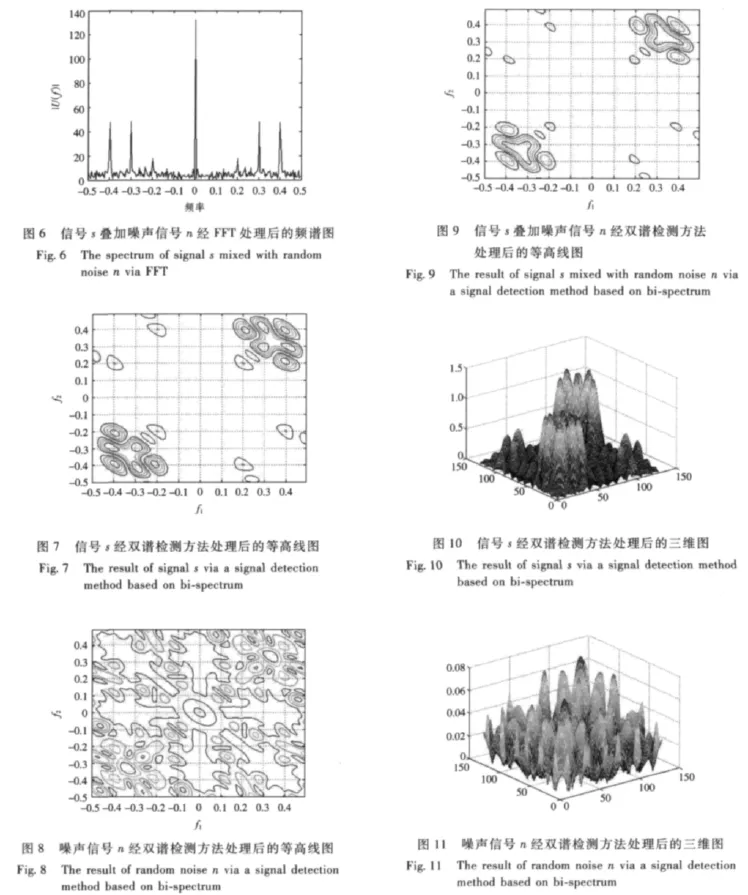
假设某一信号x(t)=sin(2πf1t)+2cos(2πf2t)+3sin(2πf3t)，其中f1=0.2，f2=0.3，f3=0.4。对该信号加入随机噪声，然后在SNR=－3 dB噪声背景情况下采用双谱方法检测该信号［6］，并与传统FFT方法进行对比。验证实验中对信号的采样点数N取256。仿真结果如图1～图12所示。

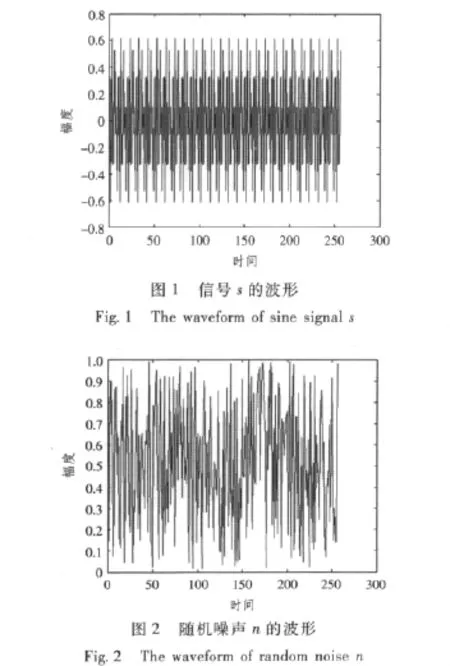
由仿真结果可以看出，基于传统FFT的检测方法，对叠加随机噪声的信号存在一定的误差。而由于高阶累计量无论对随机噪声，还是高斯噪声有明显的抑制效果，在微弱信号情况下基于双谱的目标检测方法有良好的效果。

7 结语

由于高斯噪声的高阶累计量为0，在检测混杂噪声中的微弱信号时，高阶累计量和高阶谱具有明显的优势。本文采用基于双谱的目标检测方法，对SNR=－3 dB随机噪声背景下的微弱信号进行检测，仿真结果表明，该方法效果良好。

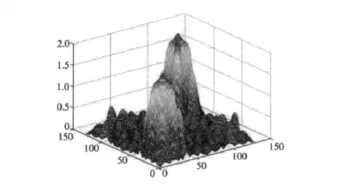
图12 信号s叠加噪声信号n经双谱检测方法处理后的三维图Fig.12 The result of signal s mixed with random noise n via a signal detection method based on bi-spectrum

［1］刘俊，张斌珍.微弱信号测技术［M］.北京:电子工业出版社，2005.26 －32.

［2］张贤达.时间序列分析——高阶统计量方法［M］.北京:清华大学出版社，1996.204 －210.

［3］吴正国，夏立，尹为民.现代信号处理技术——高阶谱、时频分析与小波变换［M］.武汉:武汉大学出版社，2003.15 －29.

［4］皇甫堪，陈建文，楼生强.现代数字信号处理［M］.北京:电子工业出版社，2003.282 －298.

［5］李志舜.鱼雷自导信号与信息处理［M］.西安:西北工业大学出版社，2004.204 －209.

［6］陈仲生.基于MATLAB 7.0的统计信息处理［M］.长沙:湖南科学技术出版社，2005.185 －207.