SCILAB在试题相关关系分析中的应用研究

曲霄红

山西大同大学教育科学与技术学院 山西 037009

0 前言

作为著名的开源科学计算软件之一，科学计算自由软件SCILAB具有运行稳定，占用计算机资源少，运行速度快等优点，已经被广泛地引进到教育研究、教学及产品开发中。而目前教育研究中一般采用价格昂贵的SPSS或MATLAB。

教育考试研究中，相关关系研究是经常要研究的内容之一，教育考试及相关调查中，一般都可以获得两个或多个变量的信息，考试研究常常需要探索这些变量之间的关系。本文在研究试题相关关系，利用SCILAB强大的数值计算功能，研究试题相关关系。

1 相关系数

1.1 相关系数介绍

在教育研究中和实际工作中，当以一个变量作为研究对象时，只需要通过集中量和差异量来描述一组数据内部的集中趋势和差异程度。但是如果研究两个变量，那么就可能不仅要关系每个变量各自的集中趋势和差异程度，还需要关系变量之间的关系。变量之间的关系要通过相关系数来描述。

教育统计学上有多个不同类型的相关系数。如积差相关系数、点二列相关系数、等级相关系数等。在相关分析中，要根据变量以及搜集的数据的具体情况来选用合适的相关系数，这里选择教育研究中常用的积差相关系数。

1.2 积差相关系数

积差相关系数也称为 Pearson系数，是英国著名统计学家K Pearson于20世纪提出的一种计算相关关系的方法，它是两个连续变量相关关系的一种参数测度。积差相关系数的基本公式是：

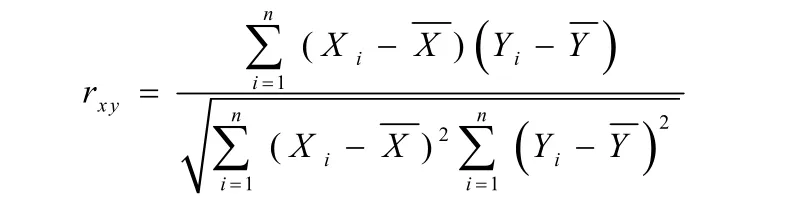
2 试题相关关系分析

试题相关关系分析研究是希望通过剖析不同试题的相关关系，判断各个试题对整个试卷测量结果贡献方面的作用。

行为变量是指考试测量的某一行为目标，将该考试中所有测量这一目标的试题得分相加，得到这一行为变量的取值。换言之，行为变量指某一科目根据不同的知识点或者测量的目标，把试卷中所有考察该知识点或者测量目标的分数相加，得到分数之和就是该行为变量的取值。

考试的不同行为变量的相关关系研究中，一般考虑以下三个关系：

(1) 不同行为变量之间的联系；

(2) 不同行为变量与考试总分之间的相关关系；

(3) 不同行为变量与考试总分减去相应变量分数后的相关关系。

不同行为变量的相关关系的思想：考试的每一个行为变量测量的是同一测量目标的不同方面，它们既有联系，又有区别，它们对测量考生的学科知识与技能、方法与能力都可以做出贡献。

3 试题相关关系分析的SCILAB实现

以 2009年贵州省贵阳市中考物理为例，根据试卷中考查的6个不同的知识点，把各个知识点得分相加，得到的总分就是6个不同的行为变量的取值。通过编写试题间相关关系分析算法得到的行为变量与总分及总分减变量自身之间的相关系数表。

3.1 试题相关关系分析的算法描述

3.2 试题相关关系分析

表1的数据是在SCILAB平台上，通过编写试题间相关关系分析算法得到的行为变量与总分及总分减变量自身之间的相关系数表。

基于不同行为变量的相关关系的基本思想，一般认为考试不同行为变量的相关关系不应太高，也不应太低，一般应该在0.3到0.6或0.7。如果两个部分的相关系数相当高，如0.85或0.9，就可以怀疑这两部分是否真的在测量不同的行为目标，可能它们实际上测量了相同的行为目标。如果是后一种情况，可能需要删掉某一部分，或者将两者部分归并。

从表1中数据得出，行为变量之间的相关关系都在0.30到0.70之间，各行为变量间的相关系数较为适中，说明各行为变量间没有明显的重叠，不需要考虑删除任何一个行为变量。这些数据也表明，这六个行为目标对于测量大纲规定的物理学科能力都起到较明显的作用，但它们各自又不明显重叠。

按照经典测量理论，某一行为变量与总分间的相关关系应该比较高，一般应在0.7以上。这是因为总分应该是考试的测量目标的更加一般的测度，每一行为变量都应该对测量目标做出较大的贡献，否则，就有理由怀疑这一行为变量是否真的与考试的测量目标一致。显然，由于总分中包含了考试测量的所有行为目标的贡献，某一行为变量与总分的相关关系实际上也受到了该行为变量自相关的影响，获得的相关系数可能偏大。

考虑到这个因素，通常的做法就是：计算某一行为变量与总分的相关系数时，从总分中减去该行为变量的分数，从表1得知，变量1、变量2、变量3和变量4与总分的相关系数均超过0.80，表明这四个变量对考试的贡献较大。

教育考试中通常用试题与总分的相关系数作为试题的区分度。从表1得出的各行为目标的区分度分别是0.89、0.80、0.86、0.82、0.77，0.75。根据试题区分度的评价标准(Eebei R.L)，这 6个试题的区分度都大于 0.40，表明试题具有良好的鉴别能力。

根据信度计算公式克朗巴赫公式，由表1中这6个行为变量计算得到的信度系数为0.90，这已经满足了大规模教育考试对考试信度系数的基本要求。

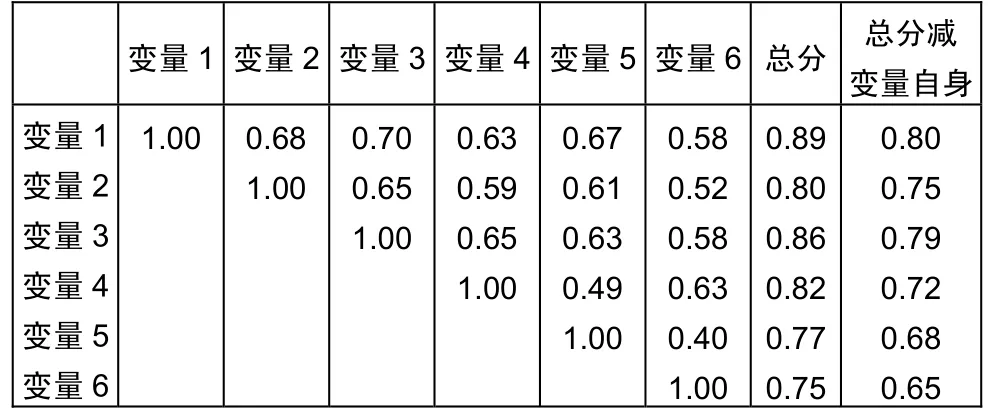
表1 行为变量相关系数矩阵表

4 结论

考试的目的是为了对考生进行教育决策提供依据，通过对试题相关关系分析可以为教育决策提供科学的信息。本实例分析表明，不同的知识点对于测量大纲规定的物理学科能力都起到较明显的作用。而且整套试题满足了大规模教育考试对考试信度系数的要求，另外试题间相关关系分析研究同样适合于试题层面的研究。

[1]李实.科学计算开放源代码软件SCILAB研究、开发与应用[M].北京:清华大学出版社.2006.

[2]刘颋.开源软件在教育中的应用[J].信息技术教育.2007.

[3]刘美宏.试卷质量分析与评估技术的研究与实现[D].沈阳:沈阳工业大学.2009.

[4]胡宝钢等.科学计算自由软件:SCILAB 教程[M].北京:清华大学出版社.2003.

[5]雷新勇.考试数据的统计分析和解释[M].上海:华东师范大学出版社.2007.