双馈风力发电机的频率控制策略研究
何飞跃,王伟胜
(中国电力科学研究院新能源研究所,北京 100192)
随着风电容量在系统中所占比重的增加,风力发电对电力系统的影响也越加明显。国内外趋势表明,风电发电系统也需要参与系统的有功控制,承担系统有功调节任务。当风力发电系统不参与系统的频率控制时,若系统负荷变化或电力发生故障,系统频率会发生变化。但由于风力发电机组不具备类似常规机组的频率特性,即不会因频率的变化而减少和增加出力,因而不会对系统的惯性做出贡献。实际上,随着风电并网容量的增加,系统总的发电容量增加,但若风电不参与频率控制,实际上参与频率控制的系统总惯性减少了,扰动或者故障消失后,系统的频率就难以恢复到合理的水平。因此,随着风电的渗透率的增加,风电也需要参加频率和AGC控制。
目前,基于双馈感应电机(DFIG)的变速恒频风电机组以其优良的有功、无功解耦控制性能成为风电主流机型[1-3],文献[4-6]研究了DFIG参与频率控制的一种方法,文献提出了采用旋转备用的方法参加频率控制。随着变速风机成为风力发电的主流机型,利用储存在风机机械系统中的动能参与频率和AGC控制成为当前的研究热点[7-9]。文献[4]提出了双馈风机惯性控制模型,以利用风机叶片储存的动能参加频率控制,但未考虑对常规电源的影响。文献[8]采用负荷模型的方法对DFIG参与频率制进行了研究。文献[9]采用附加频率控制环节的方法进行了频率控制研究,证明风电场在一定程度上参与系统频率控制。
本文建立了电力系统频率调节模型,给出了双馈风力发电机2种频率控制策略:惯性控制策略和下降速率控制策略,并对这2种控制策略的频率控制性能进行了理论分析。惯性控制策略可以使双馈发电机在频率控制发挥调节作用,但不能充分利用双馈机快速有功调节能力,同时也使常规机组的频率响应速度降低。下降速率控制策略则可以充分发挥双馈机的快速有功调节能力,并且可能充分发挥常规机组的频率快速响应特性。文中给出了双馈机组的下降速率控制策略的控制器参数优化方法,建立了含风电机组的两区域AGC控制系统,并对其进行了仿真验证,表明下降速率控制策略具有很好的控制性能。
1 机组频率控制动态模型
1.1 惯性控制策略
双馈风力发电的有功和无功控制采用解耦控制,没有常规水电/火电机组的频率特性,当系统频率变化时,不具备调整出力的能力。为了使双馈机组参加频率控制,需要在双馈机组的控制模型中加入能反映频率变化的控制环节。考虑常规机组和新能源机组的电力系统模型如图1所示,ΔPd为负荷扰动;ΔParea互联区域提供的有功功率;ΔPnc为新能源参加频率控制提供的有功出力。

图1 电力系统频率控制动态模型Fig.1 Dynamic model of frequency control in power system
考虑到电力系统有功功率平衡,有:

为了使双馈机组参加频率控制,一种可行的办法是采用惯性控制的方法。加入对频率变化和转速响应的控制环节。双馈机的控制模型如图2所示,Pel.meas为实测发电机电磁功率;ωm.ref为当前风速下的最大出力所对应的最优转速。
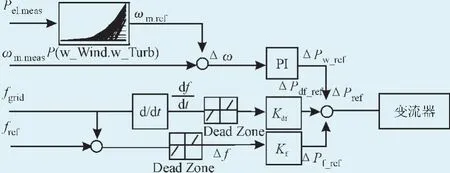
图2 DFIG惯性控制模型Fig.2 Inertial control model of DFIG
则由于考虑了频率偏差得到附加控制功率控制量为:

转速的控制采用PI控制,则考虑转速得到的附加功率控制量为:
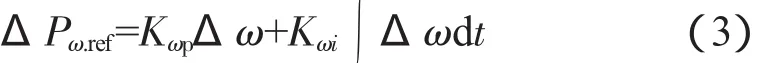
由于频率变化的暂态过程很短,可以假定在频率开始变化时ΔPω.ref=0,则非常规能源机组在频率开始变化时,提供给逆变器的频率给定为:

根据式(1)有:

代入式(4),得

由此可见,当Kdf>0时,系统提供等值惯性系数2H+Kdf比原来增大了,在这种情况,系统发生频率扰动时,风电机组参加频率控制,系统能获得较好控制性能。同时,也需要考虑频率控制的比率系数Kpf对系统的阻尼影响。当Kpf>0,虽然能够提供对频率振荡过程一个较好的阻尼性能,但同时也能会激发频率稳定过程中其他振荡模式。
总之,在这种惯性控制虽然使系统的惯性增加了,但由于不能直接提供频率支持,可能掩盖负荷的变化,导致常规电源在抑制负荷扰动的响应延迟增加;同时在这种控制方式下,没有考虑新能源中双馈发电机有功快速调节的优良特性。因此,在双馈机组的频率控制中,需要按照非常规机组的方式处理,充分利用其功率的快速调节能力,同时保证常规机组也能快速对负荷扰动做出快速响应。
1.2 下降速率控制策略
考虑常规机组的一次调频特性,当频率变化Δf,机组的有功参考增加为ΔP=Δf/R。仿照常规机组的频率特性,双馈机组的有功输出也可建立以下控制:

Washout滤波器是一种有着广泛应用的高通滤波器[11-12],它可以有效过滤稳态信号,而使高频信号通过。考虑其一维情况,其传递函数为
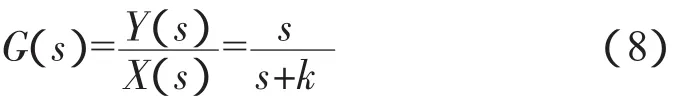
式中,k>0时Washout滤波器工作在稳定状态,k<0时Washout滤波器工作在不稳定状态。引入状态变量 w(s):

则滤波器的状态方程和输出方程为:

系统稳定时,有w0=x0/k,y0=0相当于输入信号x被冲洗掉了。考虑式(10),并将图3所示下降速率模型纳入到电力系统频率控制动态模型,时间常数k与常规电源的一次调频特性有关,其值的选取可参考常规电源的一次调频特性。
在频率扰动过程中,转速的恢复控制仍采用和惯性控制方式下相同的方式,则在这种方式下的控制模型如图3所示。图中1/R为常规机组的频率特性中的下降速率。比例系数Kωp和积分系数Kωi可以根据电力系统频率控制的性能指标进行设计,设计方法见本文2.2节。
2 互联电网频率控制动态模型
2.1 频率控制动态模型

图3 DFIG下降速率控制模型Fig.3 Drop rate model of DFIG
考虑一个两区域的AGC系统,假设常规机组为水电机组,以双馈机组为代表的风电机组参与频率控制,在系统的平衡点做线性化处理,得到风电机组参与频率控制的动态模型如图4所示。其中,两区域AGC系统模型中的ΔPnc为风电机组提供的出力,其模型在风电机组频率控制模型中。

图4 含DFIG的区域AGC控制模型Fig.4 AGC model with DFIG
选取区域1状态变量为:
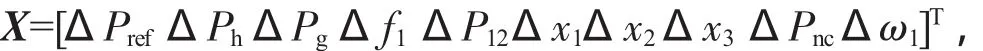
其中,ΔPref为常规机组的给定值;ΔPh为水轮机调速器导叶开度偏差;ΔPg为常规水电机组输出功率偏差;Δf为系统频率偏差;Δx1为经过频率测量环节后的频率偏差;Δx2为经过冲失滤波器后的频率偏差;Δx3为双馈机组转速积分输出偏差;Δω为双馈机组的转速偏差。则电网频率控制模型可用以下状态方程表示:

其中,W(t)为负荷扰动量,状态方程中的系数矩阵如下:

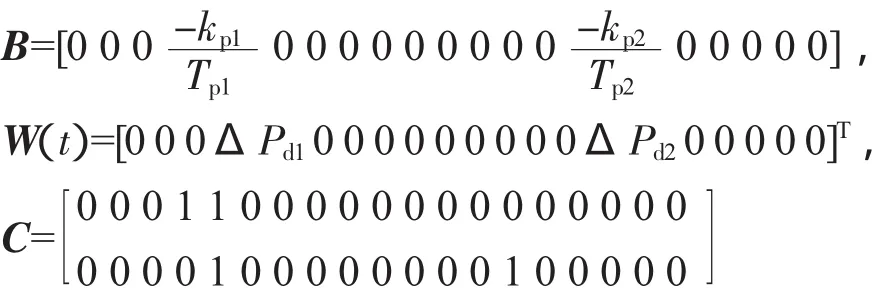
2.2 风电机组参数优化控制
为了提高风电机组参加频率控制能力,需要对风电机组中的速度控制中的Kωi,Kωp进行优化,对此可以采用误差平方积分技术(ISE,The Integral of Squared Error)来进行优化[13]。在控制系统发生扰动后,如果控制系统是稳定的,其状态变量会由扰动前的初始状态达到一个新的稳定状态。在ISE技术条件下,其动态性能指标可以用状态变量偏差的二次性能指标来表示,如下:

式中,X(t)为系统状态变量的偏差。如果在某组控制参数条件下,能够获得最小的二次性能指标J,则可以认为该组参数是最优的。在两区域的AGC控制系统中,可以选取区域控制偏差(ACE,Area Control Area)的偏差做为二次性能指标。即:

在实际控制过程中,为计算方便,需将上式中的积分运算离散化,得到在采样周期为Δt的情况下,二次性能计算指标公式为:

在实际控制过程中,可采用启发式优化算法。第一步:先对区域一、二中的DFIG的转速控制器随机选取一组参数。第二步:对区域一中Kωi、Kωp进行优化。固定一个参数,如Kωi,再对Kωp由小变大进行性能指标的计算,可求出具有最小性能指标的Kωp;再固定 Kωp,对 Kωi由大到小进行变化,即可得区域一的较优的 Kωi、Kωp。第三步:采用和第二步同样的算法,对区域二的 Kωi、Kωp进行优化,得到区域二较优的控制参数 Kωi、Kωp。第四步:利用区域一、二中经过第二、三步优化得到控制参数进行系统性能指标计算。若性能指标收敛到给定的误差范围之内,则得到两区域的最优控制参数;否则退回到第二步,再进行优化,直到误差收敛给定的范围之内。
3 仿真分析
3.1 DFIG控制策略比较
根据第2节中的DFIG控制策略,有惯性控制和下降速率控制策略2种。分别对如图1所示含DFIG的独立电力系统进行两种模式的仿真,仿真参数见文献[14]。设置负荷扰动量为2%,扰动发生在5 s时刻,仿真时间为40 s。惯性控制策略下的常规机组和DFIG的出力如图5所示,下降速率控制策略下的常规机组和DFIG出力曲线如图6所示。
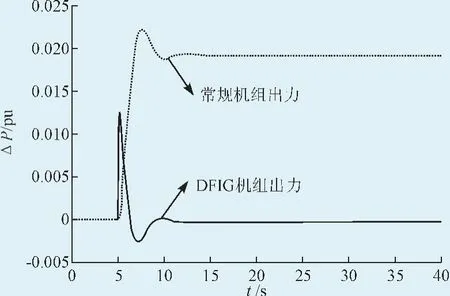
图5 惯性控制方式下的常规机组和DFIG出力曲线Fig.5 Power curve of the conventional unit and DFIG under inertia model
可以看出,在惯性模式控制方式下,常规机组和DFIG均存在一定的超调,且由于系统的总惯性加大,该模式下的常规机组的响应时间比在下降速率下的响应时间长。而采用基于下降速率的控制策略,常规机组和DFIG机组的响应时间均比较小。主要是因为在该控制策略下采用冲失滤波器来提出频率偏差的高频分量,而不是采用仿真惯性的方式来增加系统的惯性,因此既能利用常规电源的快速调频响应能力,也能充分利用DFIG的特性进行频率调节。

图6 下降速率控制策略常规机组和DFIG出力曲线Fig.6 Power curve of the conventional unit and DFIG under drop rate model
3.2 一次调频分析
对DFIG分别采用惯性控制策略和下降速率控制策略,对图1所示的独立电力系统进行一次调频的仿真。对独立电力系统设置负荷扰动,扰动设置在5 s时刻,负荷扰动量设为2%。假设在仿真过程中风速保持不变,仿真时间为40 s。分别对有无DFIG参与频率控制进行仿真,其系统的频率响应如图7所示。纵坐标表示频率偏差的相对值。

图7 一次调频频率响应曲线Fig.7 Primary frequency response curve
从图7中可看出,当DFIG采用惯性控制策略参与一次调频时,系统的频率响应过程有明显的超调量,调节时间也比较长。当DFIG采用下降速率控制策略参与一次调频时,系统的频率偏差超调明显减少,调节时间明显减小。
当发生负荷扰动时,从图8可看出,机组转速迅速下降,以释放存储叶片中的动能,增加对一次调频的功率输出,此后由于机组偏离最优转速,机组捕获的风能逐渐减小,输出功率也逐渐减小,直到在速度控制器的作用下,机组恢复到最优转速,输出功率恢复到正常值。

图8 DFIG转速响应曲线Fig.8 Rotating speed response curve of DFIG
常规机组和DFIG在负荷扰动时的功率输出如图6所示。从图中可看出,DFIG的有功输出仅在负荷扰动过程发挥作用,当系统频率恢复到稳态时,DFIG的输出恢复到扰动前的值。而对于常规电源,在发生负荷扰动时,常规机组立即增加处理,当系统达到稳态时,常规机组的输出达到新的稳态值,而不是恢复到扰动前的水平,也就是常规机组在扰动的暂态和稳态过程中都对一次调频有贡献。
3.3 两区域互联AGC仿真
对第3节中的两区域互联电网进行AGC仿真,两区域均含有DFIG风电机组,其控制参数采用第3节的方法进行优化设计,两区域的DFIG分别采用惯性控制策略和降速率控制策略,对区域一和区域二分别设置2%的负荷扰动,仿真时间设置40 s,负荷扰动发生在5 s时刻。进行仿真,得到联络线功率偏差曲线如图9所示。
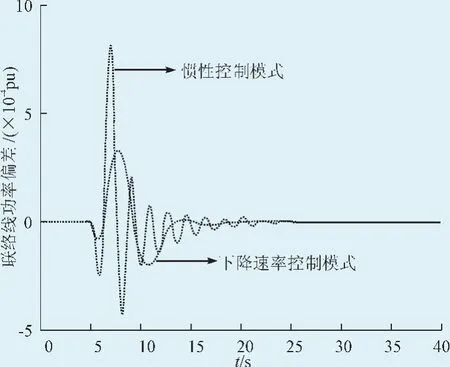
图9 联络线功率曲线Fig.9 Power curve of the tie line
从图9可看出,下降速率控制策略下的联络线偏差波动比惯性控制策略要小,调节时间也短。2种控制下的区域ACE偏差曲线如图10、11所示[15],仿真结果表明,采用下降速率控制策略,两区域的ACE偏差的波动范围比惯性控制策略下的要小,调节时间也短,频率调节的动态过程也得到了明显改善。说明DFIG能够有效利用叶片储存的能力,在频率调节的暂态过程中发挥作用,使常规机组的调节量也减小了,调节过程也缩短了,这对常规机组的运行是有利的。
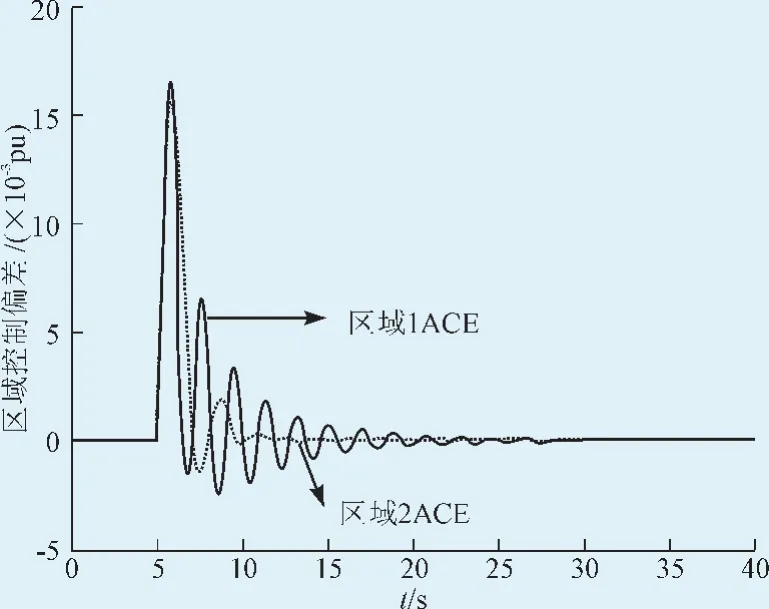
图10 惯性控制策略ACE曲线Fig.10 ACE curve of the inertia control strategy
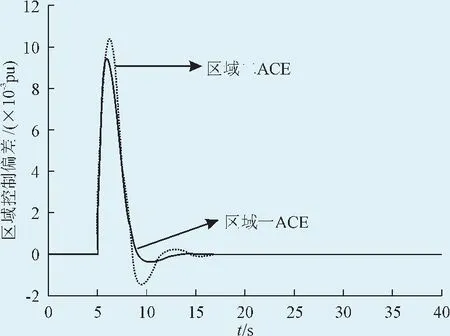
图11 下降速率控制策略ACE曲线Fig.11 ACE curve of the drop rate control strategy
4 结语
本文对双馈风力发电机参与电力系统频率控制提出了2种控制策略,惯性控制策略和下降速率控制策略。对2种控制方式进行了理论分析,分别建立了2种控制策略下的控制器,并进行了对比分析。建立了含风电机组的两区域AGC控制系统模型,仿真结果表明基于冲失滤波器的下降速率控制策略,既能够充分发挥双馈发电机的快速有功调节能力,也能充分利用常规机组的有功调节能力。
[1]李晶,宋家骅,王伟胜.大型变速恒频风力发电机组建模与仿真[J].中国电机工程学报,2004,24(6):100-105.LI Jing,SONG Jia-hua,WANG Wei-sheng.Modelling and dynamicsimulation of variable wind turbine with large capacity[J].Proceedingsof the CSEE,2004,24 (6):100-105(in Chinese).
[2]刘其辉,贺益康,张建华.交流励磁变速恒频风力发电机的运行控制及建模仿真[J].中国电机工程学报,2006,26(5):43-50.LIU Qi-hui,HE Yi-kang,ZHANG Jian-hua.Operation control and modeling simulation of ac excited variable speed constant-frequency(AEVSCF) wind power generator[J].Proceedings of the CSEE,2006,26(5):43-50(in Chinese).
[3] 苑国锋,柴建云,李永东.新型转子电流混合控制的变速恒频异步风力发电系统[J].电网技术,2005,29(15):76-80.YUAN Guo-feng,CHAI Jian-yun,LI Yong-dong.A novel variable speed constant frequency wind generation system with rotorcurrenthybrid control[J].PowerSystem Technology,2005,29(15):76-80(in Chinese).
[4]JANAKA Ekanayake,NICK Jenkins.Comparison of the response of doubly fed and fixed-speed induction generator wind turbines to changes in network frequency[J].IEEE Transaction on Energy Conversion,2004,19(4):800-802.
[5] ROG魪RIO G D A,LOPES J A P.Participation of doubly fed induction wind generators in system frequency regulation[J].IEEE Transaction on Power Systems,2007,22(3):944-950.
[6]JOHAN Morren,SJOERD W H D H,WIL L K.Wind turbines emulating inertia and supporting primary frequency control[J].IEEE Transaction on Power Systems,2006,21(1):433-434.
[7]SLOOTWEG J G,HAAN S W H D,POLINDER H.General model for representing variable speed wind turbines in power system dynamics simulations[J].IEEE Transaction on Power Systems,2003,18(1):144-151.
[8] 韩民晓,崔军立,姚蜀军.大量风电引入电网时的频率控制特性[J].电力系统自动化,2008,32(1):29-32.HAN Min-xiao,CUI Jun-li,YAO Shu-jun.Frequency control characteristics for a power system with large amounts of wind power[J].Automation of Electric Power Systems,2008,32(1):29-32(in Chinese).
[9] 关宏亮,迟永宁,王伟胜,等.双馈变速风电机组频率控制的仿真研究[J].电力系统自动化,2007,31(7):61-64.GUAN Hong-liang,CHI Yong-ning,WANG Wei-sheng,et al.Simulation of frequence control of double fed induction generator bases wind turbine[J].Automation of Electric Power Systems,2007,31(7):61-64(in Chinese).
[10]MOHAMED S S,MUNTHER A H,EYAD H A.Delaying instability and voltage collapse in power systems using SVCswithwashoutfilter-aidedfeedback[C]//AmericanControl Conference,Portland,OR,USA,2005,4357-4362.
[11]马幼捷,李小双,周雪松.基于高通滤波器技术的电力系统霍普分岔控制[J].电网技术,2011,35(7):76-79.MA You-jie,LI Xiao-shuang,ZHOU Xue-song.Hopf bifurcation control of power system based on high-pass filtertechnologysystem[J].PowerSystemTechnology,2011,35(7):76-79(in Chinese).
[12]BALARKO Chaudhuri,RAJAT Majumder,BIKASH C P.Wide-area measurement-based stabilizing control of power system considering signal transmission delay[J].IEEE Trans Power System,2004,19(4):1971-1979.
[13]BHATTACHARYA K,KOTHARI M L,NANDA J,et al.Tuning of power system stabilizers in multi-machine systems using ISE technique[J].Electric Power Systems Research,1998,46:119-131.
[14]KUNDUR P.Power system stability and control[M].New York:McGraw-Hill,1994.
[15]段献忠,何飞跃.考虑通信延迟的网络化AGC鲁棒控制器设计[J].中国电机工程学报,2006,26(22):35-40.DUAN Xian-zhong,HE Fei-yue.Networked AGC robust controller design in consideration of communication delay[J].Proceedings of the CSEE 2006,26(22):35-40 (in Chinese).

