正则矩阵补偿的部分线性模型解法及其性质
刘 靖
湖南涉外经济学院,湖南长沙 410073
0 引言
部分线性模型又称之为半参数模型,通常由两部分函数组成,一是能够参数化建模的函数模型(通常是线性模型),二是非参数模型。部分线性模型由Engle(1986)研究电力需求和气候条件之间关系时提出的[1]。部分线性模型一经提出,立刻展示了它强大的生命力,在统计学界得到了充分的肯定和研究[2-4]。因为相比线性模型它更能表述客观真实的实际情况。对于已知特征并能建模的部分,采用参数模型表述,如Xβ,其中β是待估参数,X是模型结构矩阵。对于未知特征不能参数化描述的部分,采用非参数模型描述,如 g( T)。相对传统的线性模型,g ( T)用来刻画未知模型或者不确定性误差影响部分。因此,部分线性模型要比线性模型更准确反映真实状态。部分线性模型的求解方法和结构特性一直是统计学界探求的重要方向,本文将研究基于正则化矩阵补偿的部分线性模型估计方法及其性质。
1 基于正则化矩阵补偿的部分线性模型估计方法及性质
1.1 基于正则化矩阵补偿的部分线性模型估计原理及方法
简记部分线性模型为

其中X是模型结构矩阵 ,β = (β1, β2,… , βd)T是待估参数 ,ei为i.i.d.随机误差 ,且 E (ei) = 0,E (ei2)= 1,g(⋅)是定义在闭区间[a,b]上的未知函数。误差方程可记为
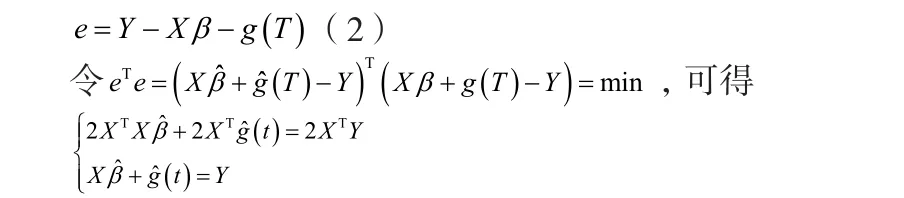
由于法方程系数矩阵奇异,因此方程的解不唯一。
采用补偿最小二乘准则对极值方程进行修改,
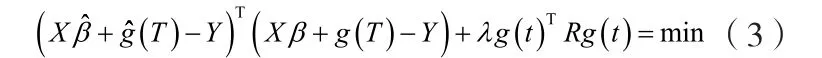
根据非参数模型的特征,选择相应的正定矩阵作为正规化矩阵R,组成二次型 gˆ( t)TRg( t)。二次型刻画非参数分量gˆ( t)的光滑性度量。当光滑性程度超高时,模型就变为一般的常值误差估计模型;当光滑性为0时,非参数分量值等价与观测数据,此时非参数量在模型中占的比重在100%,参数值β对模型没有任何贡献,显然不符合实际情况。因此,合理选择二次型具有重要意义。
对方程(3)采用拉格朗日条件极值方法,构造函数:
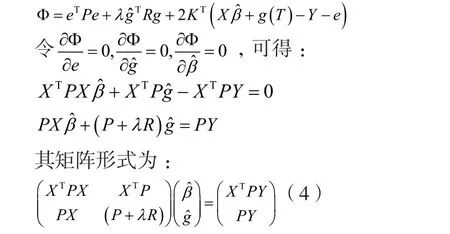
当矩阵R为正定矩阵时,式(4)的系数矩阵是正定可逆矩阵。因此有唯一解。则有,
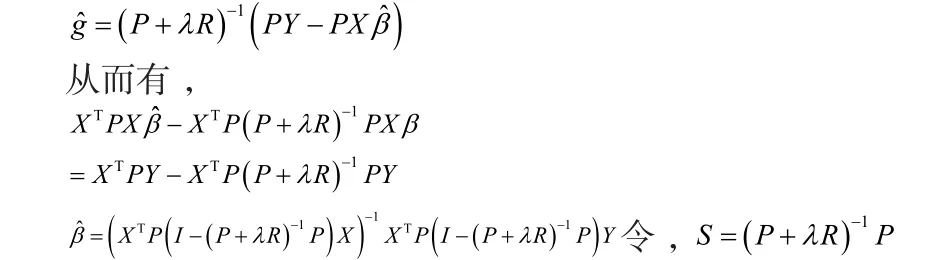
则基于正则矩阵补偿的部分线性模型估计值为:

1.2 基于正则化矩阵补偿的部分线性模型估计性质



下面证明S(I-XM)不是单位矩阵,用反证法。设S( I-XM )=I,右乘得到 :
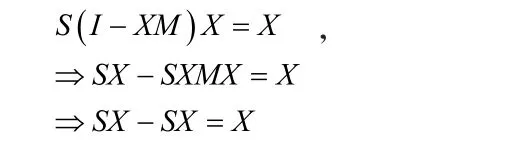
定理 [5]:当λ满足一定条件时,在MSE准则下,补偿最小二乘估计精度要优于经典最小二乘估计精度。
2 结论
部分线性模型求解方法主要包括基于最小二乘的偏残差估计、三角级数估计、偏核光滑估计、分块多项式估计、小波估计、以及本文研究的正则矩阵补偿的估计方法。事实上,几种方法的原理是一致的,都是假设部分线性模型的非参数部分在闭区间[a,b]上是二次连续的,因此,基于维尔斯特拉斯定理,一定能够用有限个参数进行无限逼近。从而将非参数问题巧妙地转换为参数问题。本文研究的基于正则矩阵的补偿方法,也是利用该原理进行计算的。
[1]Engle,R.E.,Granger,C.W.J.et al.Semiparametric estimates of the relation between weather and electricity sales[J].JASA.,1986,81:310-320.
[2]Bickel,P.J.,Klaasen, C.A.J.,et al.Efficient and adaptive estimation in semi-parametric models[M].Baltimore: John Hopkins Univ.Press, 1993.
[3]Heckman, N.E.Spline smoothing in a partly linear model[J].J R.Statist.Sec.B, 48:244-249 ,1986.
[4]Rice, J.,Convergence rates for partly linear models[J].Statist.& Probab.Lett.,4, 1986: 203-208.
[5]潘雄.半参数模型的估计理论及其应用[D].武汉大学博士论文,2005.

