偏置正交面齿轮的几何设计及三维造型

魏冰阳，袁群威，吴 聪

(河南科技大学机电工程学院，河南洛阳471003)

0 前言

面齿轮传动是一种圆柱齿轮与圆锥齿轮相啮合的齿轮传动形式［1-3］，因此，面齿轮可应用于正交与非正交场合的传动。但人们常常忽视面齿轮传动的另外一种形式——小轮偏置面齿轮传动。其实这种传动形式能大幅度拓宽面齿轮传动的应用领域，它为设计者提供了更大的发挥空间，小齿轮轴线的下偏置有利于降低机体重心的高度，采用跨式支承，能大幅度提高系统的刚性，且这种设计具有较大的重合度。文献［1-3］对面齿轮传动的啮合理论做了研究，从几何原理的角度获得了避免面齿轮根切和齿顶变尖的条件。文献［4-11］则由产行齿轮展成面齿轮过程中啮合角度变化出发，对面齿轮齿宽的研究做了进一步的分析。本文拟利用齿轮啮合原理，推导出偏置面齿轮的齿面方程，轮齿根切和齿顶变尖的限制条件，计算面齿轮受限的最小内半径和最大外半径，并在给定参数下进行面齿轮的三维造型。

1 偏置正交面齿轮齿面方程

1.1 加工坐标系

偏置正交面齿轮的加工是把插齿刀从面齿轮对称轴线向一侧移开一个距离，所加工出的面齿轮即能和轴线偏置的圆柱齿轮啮合。刀具和面齿轮的坐标系如图1所示，坐标系Ss，S2分别固结于刀具和面齿轮，坐标系Sa，Sh为辅助坐标系，E为偏置距，Ss和S2分别绕其z轴旋转形成展成关系，其旋转角分别为φs和φ2，φ2=zs/z2φs。由图1可以求得坐标变换

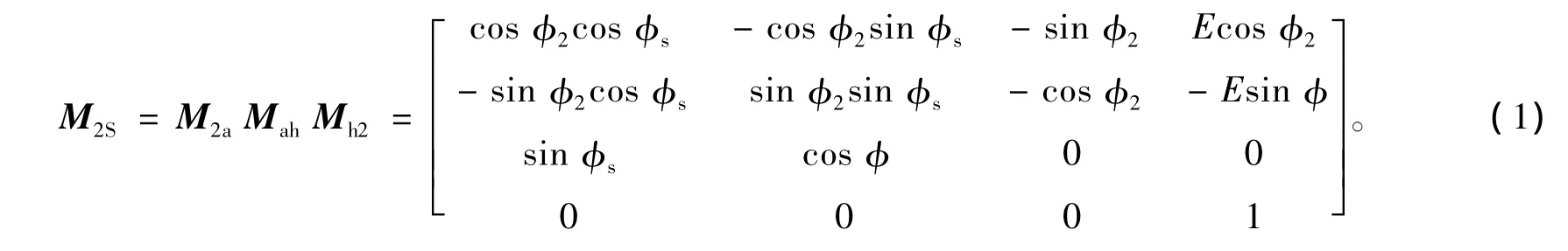
刀具渐开线齿形如图2所示，刀具的齿面方程为

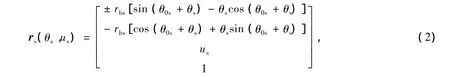
式中，rbs为刀具基圆半径;θs为渐开线展角参数;θ0s为齿宽在基圆上的对应转角，θ0s由下式确定

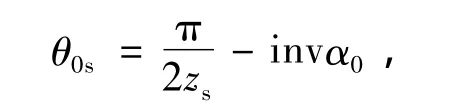
±号分别对应于刀具齿槽两侧的渐开线a-a，b-b，其中，zs为刀具齿数;α0为刀具压力角;invα0为压力角的渐开线函数，invα0=tan α0- α0。

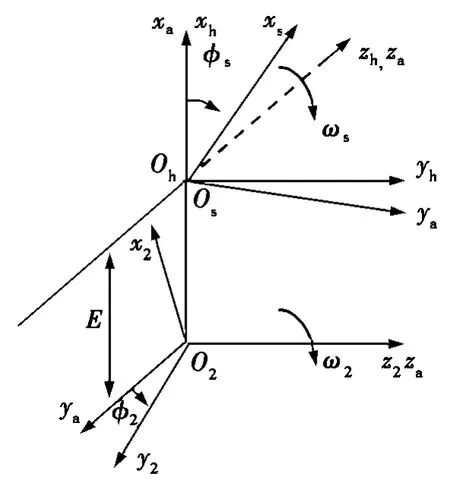
图1 面齿轮加工坐标

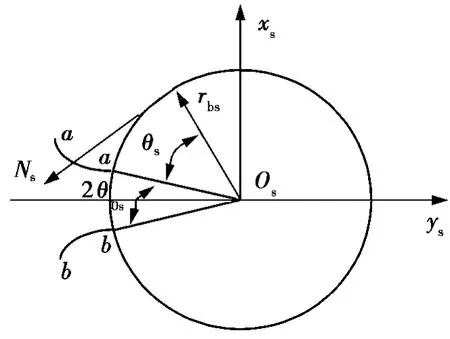
图2 刀具渐开线齿形

刀具齿面的单位法矢为

1.2 面齿轮的齿面方程

设刀具与面齿轮的接触点为P，P点随同坐标系Ss和S2的运动速度分别为vs和v2，把P点的相对运动速度表示在坐标系Ss下为

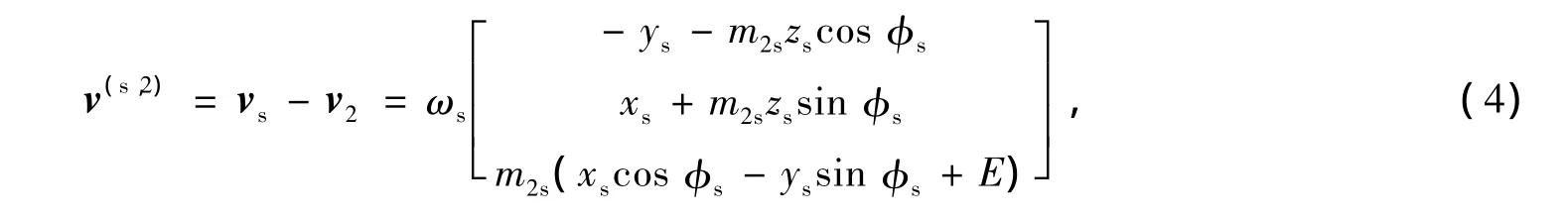
其中m2s=ms/m2。

得到

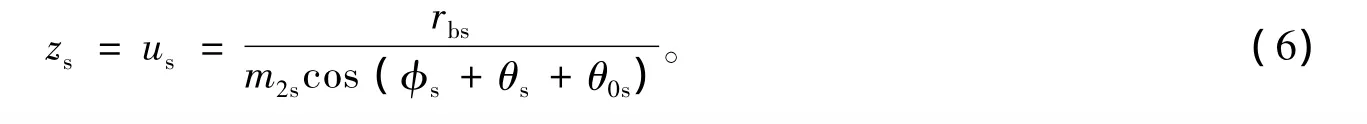
面齿轮的齿面方程可由式(6)代入下面的方程求得

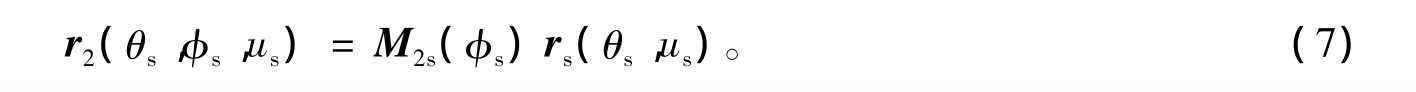
利用式(1)和式(2)得面齿轮的齿面方程为

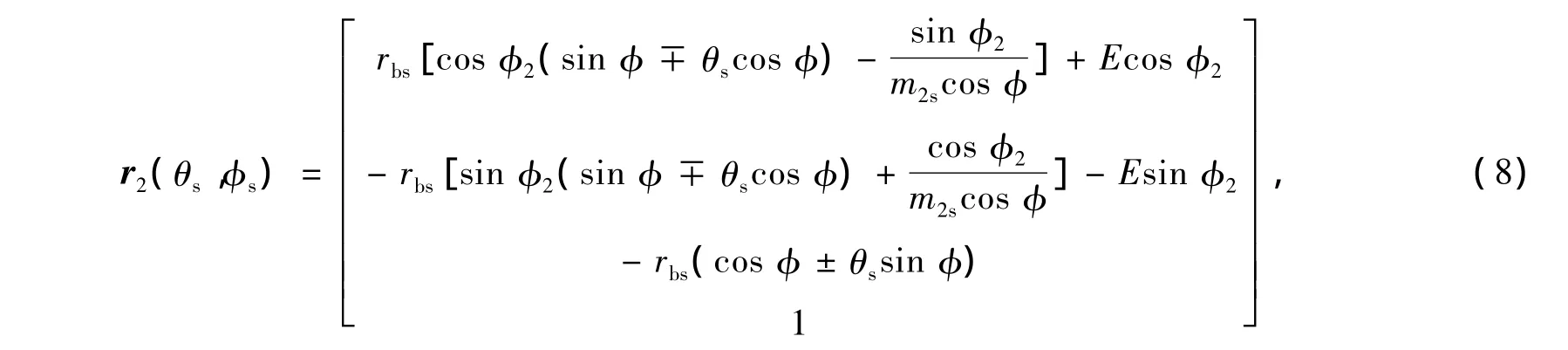
其中 φ = φs± (θs+ θ0s)。

2 面齿轮不发生根切的最小内半径

面齿轮的最小内半径是由根切的界限条件来确定的，避免根切可以通过限定刀具齿面Σs来实现，其限制根切的条件为

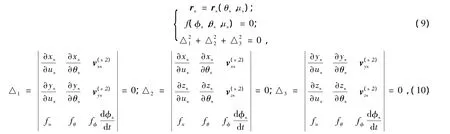
式中，fu、fθ、fφ是啮合方程分别对 us、θs、φs求导是相对速度在 Ss各轴的分量。根切临界点就是根切极限处与刀具齿顶的交点，所以

由于偏置正交面齿轮的两侧轮廓是不对称的，故会有两个极限值R1a，和R1b，在设计中，取两者的最大值，所以

3 面齿轮不发生顶尖的最大外半径

把坐标系S2沿z2轴线平移到面齿轮齿顶的位置，建立一个新的坐标系Sg，如图3所示。将面齿轮的齿面方程转换到坐标系Sg下，即

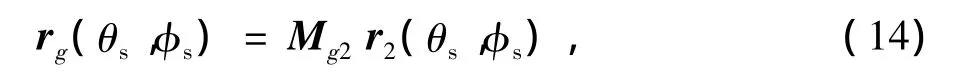
式中Mg2是从S2到Sg的坐标变换矩阵，

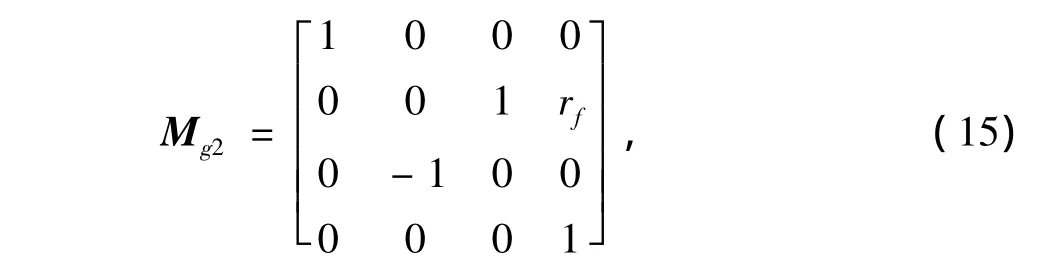
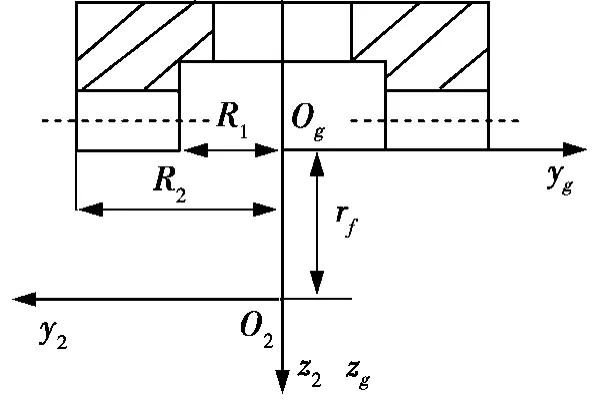
图3 齿面的另一坐标系

式中rf为刀具的齿根圆半径。

齿顶变尖是指轮齿的两侧齿面相交以后使得齿顶的厚度等于零或者接近于零，考虑到偏置正交面齿轮两侧轮廓的不对称性，轮齿变尖的条件为

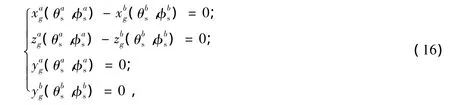
式中，上标a和b分别对应左侧和右侧齿廓的参数，解方程(17)即可得到极限点坐标，偏置正交面齿轮不变尖的最大外半径为

4 偏置正交面齿轮的三维造型

4.1 参数的选择和计算

基本参数:模数m=3 mm，面齿轮齿数z2=89，小轮(渐开线标准直齿圆柱齿轮)齿数zs=25，压力角α0=20°，齿顶高系数=1，顶隙系数c*=0.25，偏置距E=25 mm，计算可以得到R1=133 mm，R2=156 mm。

4.2 网格规划

网格划分一般采用的原则:齿长方向取等距的9列，齿高方向取等距的5列，那么整个齿面上连成网络，节点有45个，如图4所示，考虑到偏置正交面齿轮的两侧轮廓的不对称性，需要分别对齿廓两侧规划。网格上任意一点的坐标为(Yij，Zij)，i=1～5，j=1～9，

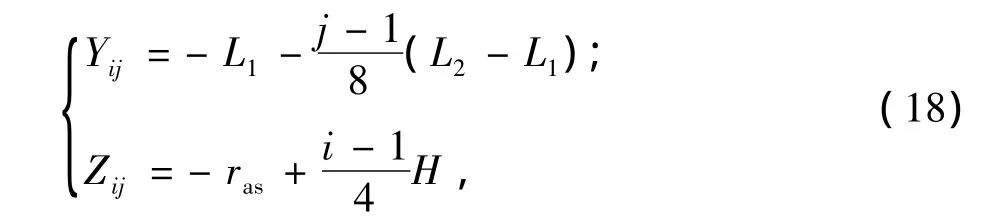
齿面上任意一点的坐标(x2，y2，z2)于旋转投影面内对应的坐标满足以下关系式

利用Matlab求解方程(19)，分别得到两侧齿廓的三维坐标点。

4.3 创建实体

将计算得到的坐标点保存成IBL文件，导入Pro/E，生成偏置正交面齿轮的齿面曲面，将曲面封闭实体化处理得到齿轮的单个轮齿，如图5所示，将曲线隐藏，对轮齿进行阵列即可得到整个齿形，小轮是标准圆柱齿轮，可以从数据库中直接调用完成装配，如图6所示。

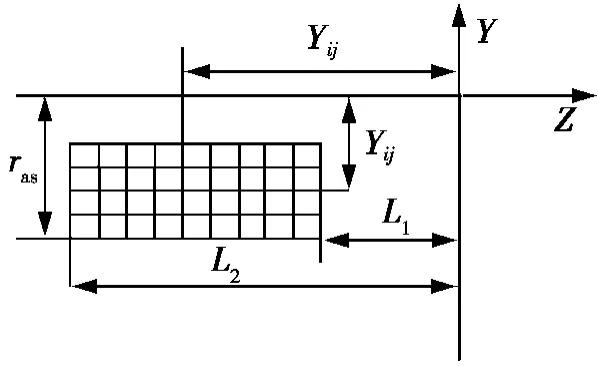
图4 面面网格

图5 面齿轮轮齿

从图5中可以看出:面齿轮的齿顶没有变尖，齿根未发生根切，说明上述的推导和几何计算是正确的。由于偏置面齿轮的齿廓两侧不对称，轮齿纵向出现了一定的倾斜，这对增加齿轮副的重合度有利。

5 结论

通过对偏置正交面齿轮齿面方程的推导，得出了齿顶变尖与根切的限制条件，通过编写相关程序，仿真模拟完成了偏置面齿轮的几何设计，三维啮合装配，其结果验证了本文理论推导和计算的正确性。面齿轮副的三维造型及其装配为今后进一步的啮合分析、有限元分析、强度计算奠定了基础。

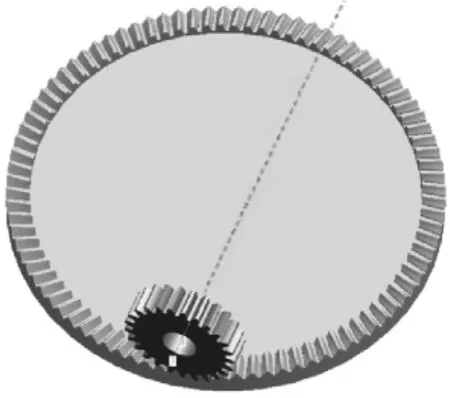
图6 偏置面齿轮的装配图

［1］Faydor L L，Ignacio G P，Alfonso F，et al.Generation and Stress Analysis of Face-gear Drive with Helical Pinion［J］.Computer Methods in Applied Mechaics Andengineering，2005，194:3870-3901.

［2］Litvin F L，Fuentes A，Howkins M.Design，Generation and TCA of New Type of Asymmetric Face-Gear Drive with Modified Geometry［J］.Comput Methods Appl Mech Engrg，2001，190:5837-5865.

［3］Faydor L L，Alfonso F，Claudio Z，et al.Design，Generation，and Stress Analysis of Two Versions of Geometry of Face-gear Drives［J］.Mechanism and Mechine Theory，2002，37:1179-1211.

［4］黄丽娟，朱如鹏.基于斜齿小齿轮的面齿轮生成研究［J］.机械工程师，2007，36(1):29-31.

［5］李龙，朱如鹏.正交面齿轮弹流润滑分析［J］.机械工程师，2007，36(2):63-65.

［6］李政民卿，朱如鹏.正交面齿轮齿廓的几何设计和根切研究［J］.华南理工大学学报:自然科学版，2008，36(4):754-758.

［7］沈云波，方宗德，赵宁，等.斜齿面齿轮齿宽设计［J］.航空动力学报，2008，23(4):754-758.

［8］赵宁，曾晓春，郭辉，等.斜齿面齿轮仿真及其轮齿接触分析［J］.航空动力学报，2008，23(11):1927-1932.

［9］贺鹏，刘光磊.面齿轮数值仿真［J］.科学技术与工程，2007，7(12):2956-2958.

［10］王延忠，熊巍，张俐，等.面齿轮齿面方程及其轮齿接触分析［J］.机床与液压，2007，35(12):7-9.

［11］杨建军，魏冰阳，周彦伟，等.准双曲面齿轮设计加工集成系统的开发［J］.河南科技大学学报:自然科学版，2004，25(5):17-20.