水声宽带信号波形预报技术研究
唐 帅, 笪良龙, 谢 骏
(海军潜艇学院, 山东 青岛 266071)
随着精细化水下声信息特征的需求日趋增加,宽带波形预报已成为信号级仿真的核心研究内容,为了更深入地研究水声信道对信号传输以及水声装备探测性能的影响, 传统的从能量损失角度考虑的方法显然已经无法满足研究需求。
长期以来, 水声信道的建模和仿真主要是针对低频、相对带宽较窄的信号进行研究, 缺乏对宽带水声信道的建模和仿真研究, 更缺乏能够满足波形快速预报需求的宽带水声信道模型。水声传播建模通常是从频域波动方程出发, 求解特定条件下的声压场。研究海洋宽带信号的传播波形仿真问题, 首先需要进行宽带传播模型的研究。宽带传播模型主要分为频域方法和时域方法两大类[1], 如图1所示。

图1 宽带传播模型Fig. 1 Schematic of two approaches to broadband modeling
一般说来, 海洋信道是时变、空变的随机信道,但是当观察或处理时间不是过分长时, 海洋信道可以作为时不变信道, 本文就是基于此假设, 开展宽带信号波形预报研究。本文分析了宽带传播模型的基本原理和实现技术, 研究了基于波束位移射线简正波(BDRM)的频域傅立叶合成波形预报算法和基于 BELLHOP射线模型的时域波形预报算法, 并针对典型环境条件, 进行了宽带波形仿真分析, 并对模型的适用性进行了讨论。
1 宽带传播模型
1.1 频域宽带传播模型
宽带信号的传播波形仿真可根据下式得到:
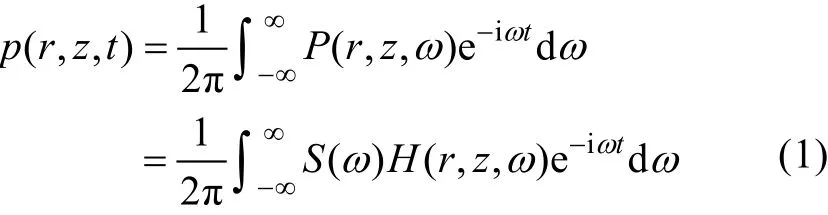
p(r,z,t)是接收点(r,z)t时刻接收到的信号波形,p(r,z,ω)是其频谱。S(ω)是信号源的频谱, 其时域波形为s(t),H(r,z,ω)是频域海洋信道传输函数, 可采用任何一种频域传播模型得到, BDRM 理论是一种十分有效的声场计算方法[2-3], 具有较高的精度, 较快的计算速度, 所以本文仿真分析中是基于 BDRM理论实现频域宽带建模。
在实际仿真过程中需要注意以下问题。实际信号源信号s(t)是带限信号, 即
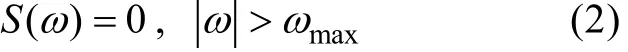
因此(1)式变为:
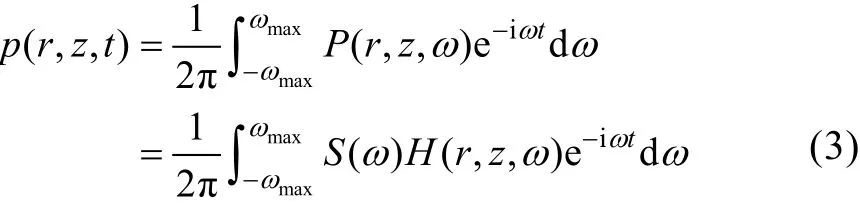
从(3)式可以看出, 该式右边在实际计算中需要对信道传输信号的频谱进行截断。这个截断相当于在时域用某个核函数去卷积信号源波形, 这必然扭曲信号并导致相位截断。为了改善结果, 需要使用Hanning窗去改善信号的突变。在频域我们采用Hanning窗与信号频谱相乘。Hanning窗定义如下。
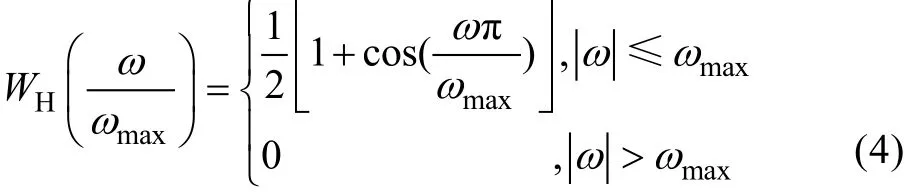
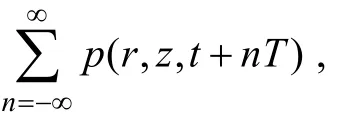
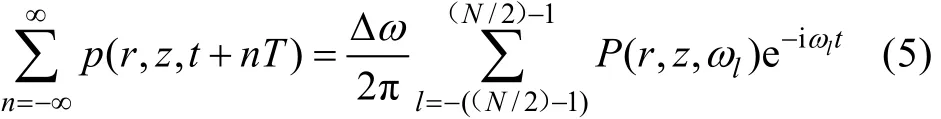
其 中,l= -( (N/ 2) - 1 ),… ,- 1 ,0,1,…(,N/2) -1,ωl=lΔω。上述结果也可根据Poisson求和公式直接给出。
现在对(5)式进一步进行时域离散处理, 对(5)式两边同时乘上脉冲采样函数, 得到

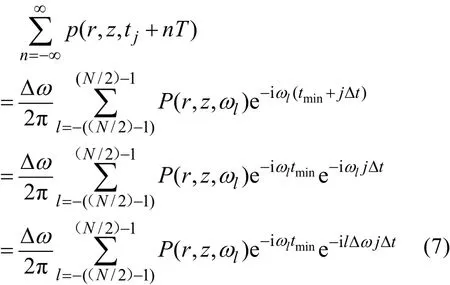
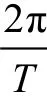
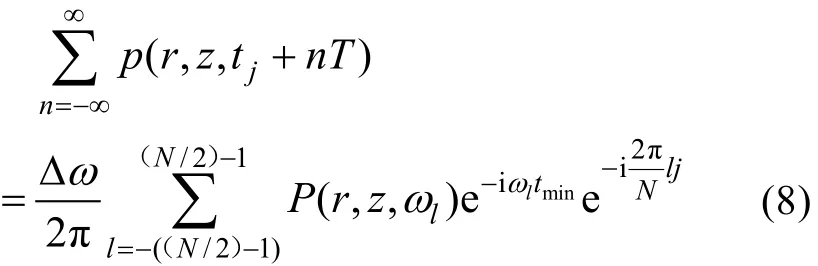
接收信号为:

如果频域采样间隔远大于最低频率, 低频信号存在, 时间信号将产生混叠。为了避免混淆, 需要频率采样间隔非常小, 频率采样点变多, 计算H(r,z,ω)花费时间变大。
1.2 时域宽带传播模型
时域宽带传播模型这里主要介绍射线模型的基本原理[4-5]。设单个本征声线所作贡献的单频表达式,即

式中A(l)是由声线管横截面积决定的幅度,τ(l)使沿声线路径的相位延迟:

进一步假设损失与频率无关, 因而幅度项A(l)也与频率无关。对于中心频率为f0的窄谱声源, 我们可以根据对频率f0得到的损失来计算A(l)。另一方面,如果损失与频率有简单关系, 只要微小的修改就可以继续进行下面的推导。
如前所述, 时域解可以通过傅立叶合成得到, 即
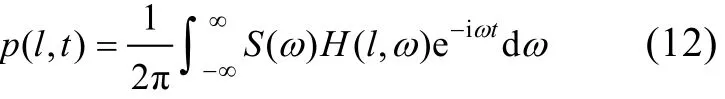
式中S()ω是声源的谱。代入H(l,)ω的声线表达式得
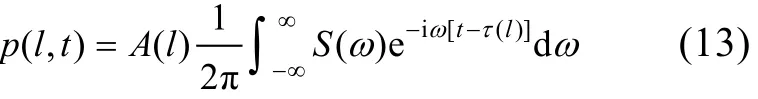
也就是
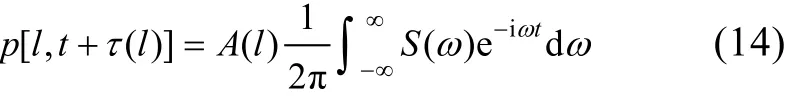
若把谱积分看成是逆傅立叶变换, 故有
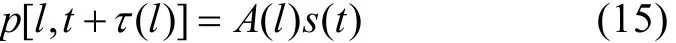
不失一般性, 上式可写成如下形式
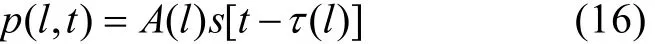
显然, 某号声线的接收信号就是声源信号波形按幅度按照A(l)加权, 并伴有τ(l)延迟的结果。因此有
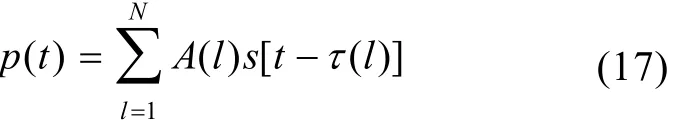
如果声源为δ脉冲, 上式变为

上式即为水声信道的系统响应函数,N为有效声线的个数。对其求傅立叶变换得到:
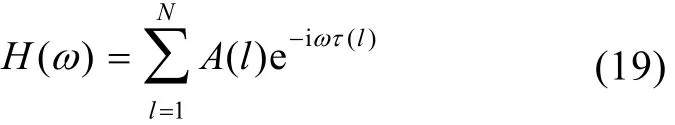
从射线声学的角度, 根据(18)式水声信道信号处理系统的结构可用图2表示。

图2 基于射线的水声信道传输系统结构图Fig. 2 Underwater acoustic channel transmission system on the basis of ray model
根据数字信号处理知识可知, 图中对脉冲信号进行延迟、加权和求和过程是典型的时域数字滤波器设计过程[6], 而且这种延迟求和会导致系统频域幅度响应函数呈现“梳状滤波器”形状, 实际上水声信道响应函数的确是呈现“梳状滤波器”结构的[1]。这主要由于本征声线掠射角是离散的, 在一个连续的时空中, 声传输过程被表征成了离散化的数字系统。
2 数值结果分析
2.1 典型浅海环境宽带波形仿真结果分析
图3给出了典型浅海负跃层环境, 海深 75 m,表面等温层厚度13 m, 声速为1 536 m/s, 负跃层厚度14 m, 声速从1 536 m/s线性减小至1 480 m/s, 温跃层下是一个等温层, 声速为 1 480 m/s, 海底模型采用均匀海底, 海底参数为: 声速为 1 628 m/s, 密度为1.6 g/cm3, 吸收系数为1.09dB/λ。

图3 典型浅海负跃层环境Fig. 3 Typical shallow water environment with a negative thermocline
图4是在图 3所示环境条件下 BDRM与BELLHOP仿真接收波形比较图, 声源深度25 m, 接收深度20 m, 图4(a)是中心频率50 Hz的脉冲声源信号及频谱; 图 4(b)是 30 km处接收波形, BDRM 与BELLHOP仿真接收波形相关系数为80.3%。从图4(b)中可以看出, 两模型预报波形主要在第二个波包后沿差异较大, 前沿主要是高频的贡献, 后沿更多是低频的贡献, BELLHOP对较低频率声线的预报有较大误差; 为进一步验证这一想法, 将信号中心频率调整到150 Hz, 宽带50 Hz, 接收波形仿真结果如图4(c)所示, BDRM与BELLHOP仿真接收波形相关系数为高达99%; 图4(d)是距离为22 km时的仿真结果,接收波形相关系数为 86.4%, 相关系数变小的原因是两模型计算时延误差引起的。
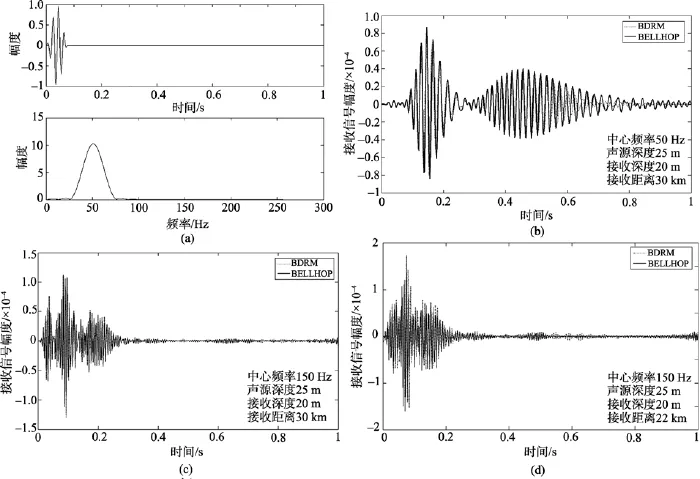
图4 BELLHOP与BDRM浅海预报接收波形对比Fig. 4 Shallow water forecast waveform received contrast BDRM with BELLHOP
2.2 典型深海环境宽带波形仿真结果分析
图5是典型深海声速剖面, 该波导的声道轴位于 1 400 m, 声速为 1 500.1 m/s, 海面下声速为1 548.5 m/s, 海深5 000 m处的声速为1 551.9 m/s。海底模型与浅海模型相同。
图6是在图5所示深海声道环境下, 声源信号为δ脉冲经过100~1 000 Hz带宽的8阶Butterworth滤波后的信号, 声源深度200m, 接收距离分别为25,50和100 km时, 不同接收深度上BDRM与BELLHOP仿真接收波形比较图, 两模型预报结果相关系数不低于95%, 预报结果吻合较好。
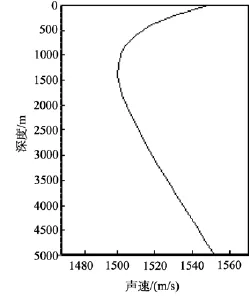
图5 典型深海声道环境Fig. 5 Typical deep-sound channel environment
通过上述两种不同海洋环境中预报波形比对发现, 在一定条件下, 两种模型具有同等的预报精度,均给出了稳定的梳状多途结构, 而且在深海会聚区内, 同样得到了较好的预报精度。由于射线模型通过一次计算就能得到所有本征声线的幅度和延迟, 能够很方便快速的构造出信道传输函数, 相对于简正波模型来说, 更适合于高频深海宽带信道的仿真问题; 利用频域方法建模, 频带宽度较大时, 计算时间较长, 无法满足仿真平台快速预报的要求, 在工程实现过程中可采用频域近似展开方法[7], 实现本征值和本征函数的快速计算, 从计算过程角度实现了模型优化, 同时, 从宽带模型的计算实现出发, 将串行宽带模型并行化, 通过高性能并行计算平台进行计算, 也可实现快速求解频域宽带模型的目的。

图6 BELLHOP与BDRM深海预报接收波形对比Fig. 6 Deep water forecast waveform received contrast BDRM with BELLHOP
3 结论
本文分析了宽带传播模型的基本原理和实现技术, 研究了基于 BDRM简正波模型的频域傅立叶合成波形预报算法和基于 BELLHOP射线模型的时域波形预报算法, 并针对典型环境条件, 进行了仿真分析比对, 通过比对发现, 在一定条件下, 两种模型具有同等计算精度, 可满足不同条件下的信号波形预报需求, 为深入研究水声信道对信号传输以及水声装备探测性能的影响提供了有效途径。
[1]Paul C E.水声建模与仿真[M].蔡志敏, 宋昕, 姚万军,等译.北京: 电子工业出版社, 2005: 34.
[2]张林.波束位移射线简正波理论在双轴海洋声道中的应用[J].声学技术, 2005, 3: 167-169.
[3]张林.基于BDRM理论的深海声场快速预报研究[J].应用声学, 2007, 4: 239-243.
[4]Thorsos E I, Henyey F S, Williams K L. Simulation of temporal and spatial variability in shallow water propagation[D]. University of Washington, 2002:337-344.
[5]李永平, 毛卫宁.基于分层海洋射线传播模型的接收信号仿真[J]. 声学与电子工程, 2003, 1: 12-14.
[6]Ulrich K. 信号处理的交互式多媒体教程[M]. 李秀梅,肖泳,毕国安译. 北京: 清华大学出版社, 2008: 263-267.
[7]唐帅, 笪良龙, 谢骏.负跃层浅海中宽带声场预报的快速算法[J].声学技术, 2009, 增刊: 1-3.

