RCS测量雷达伺服控制问题浅析

江戈

（中国飞行试验研究院，陕西 西安 710089）

0 引言

在制导武器的攻防对抗中，从发现、跟踪、识别、拦截直到杀伤目标的过程,都牵涉到对目标信号特征的研究。其中RCS(雷达散射截面)既是表征目标对雷达波散射能力的量，又是频率、极化、视向角等的函数，同时还是表述目标电磁散射特性的一个基本参数，因此，如何精确获取它十分重要。

影响RCS动态测量精度的因素除频率稳定度、功率稳定度、动态范围等指标外，还有数据采集系统的误差、航迹与航姿记录系统误差、时间同步误差等因素。而测量雷达引导控制问题同样会影响测量精度，若飞行中目标不在波束中心，则目标的照射功率就有起伏，这和功率稳定度的影响相似。RCS动态测量还需满足如下条件：

1)平面波近似:一般要求在目标径向和横向上，入射场的变化在允许值之内。幅度变化一般可以忽略，要求相位变化<π/8，即横向尺寸为D的目标距离必须大于远场距离：R＞,对于尺寸15米的目标，波长3 cm时，远场距离为：15 km。

3)信噪比要求：雷达回波是背景与目标回波场的矢量和，当目标的响应小于背景噪声，或具有同样幅度量级，测量就会有明显的误差。所以若要测量精度为1 dB，信噪比需大于20 dB。

总之，RCS的飞行试验要求整个动态测量系统工作稳定可靠，包括配套的搜索跟踪雷达和引导拖动系统。

1 雷达引导问题

1.1 系统结构和现象

由于改造后的S/X双波段测量雷达没有搜索跟踪功能，所以必须有指示目标位置的引导设备：由C波段高精度航迹观测雷达实时将目标位置信息送给引导处理计算机，经坐标变换和时延修正，解算出测量雷达应指向的角度，通过串口送给测量雷达的拖动及数采计算机。系统方框如图1所示。

由于S/X波段雷达只能输出与输入模拟信号，不能接受外部数字化引导信息，所以将S/X波段同步机信号通过同步数字变换器转换成角度与引导角度相减得到误差角，D/A转换后输出误差电压，再由信号调理单元放大后去控制S/X波段雷达指向目标。

在实际使用中，发现S/X波段雷达偏离目标较大角度时，天线不能稳定下来，而是绕目标点来回摆动，且幅度越来越大无法停止。另外在跟踪过程中若目标以较大角速度运动，就会丢失目标。也就是说引导系统的稳定性差。下面简要分析S/X波段雷达天线控制系统，以了解系统传递函数的形式。

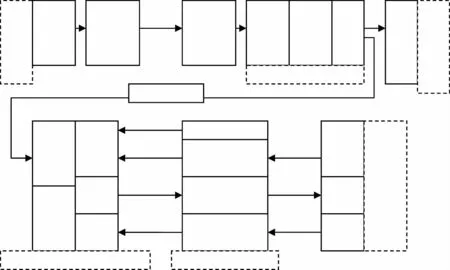
图1 RCS测量雷达引导系统图

1.2 系统传递函数

S/X波段雷达伺服控制系统是采用自整角机的位置随动系统，天线驱动电机是无刷直流伺服电机，简化的原理框如图2所示。

确定各部分传递函数：

1)小角度差内，自整角机的输出电压近似与失调角成正比，所以自整角机的传递函数为比例环节，即：

2)相敏放大器将交流误差电压转换成直流电压，若相敏放大系数为Kp，滤波时间常数为Tp，则传递函数为：

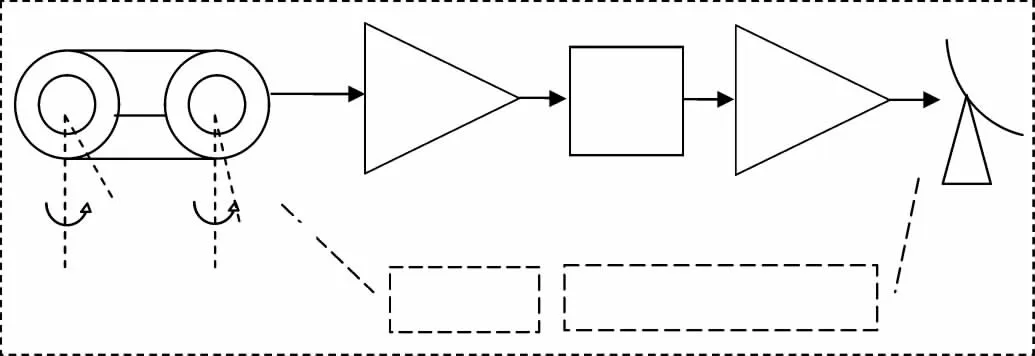
图2 雷达伺服控制系统原理图

其中Ce是电机电动势系数，Tm是电机的机电时间常数，T1是电枢回路的时间常数，一般很小。

5)减速器的输入量是执行电动机的转速n（或者角速度），单位r/min，输出量为机械转角θm（°），θm与n的关系为积分关系：若取时间t的单位为s，则为：取拉氏变换得到传递函数：Wg，减速器为积分环节，式中Kg=6/i为减速器的放大系数。

至此，除校正网络以外的各环节传递函数已知，设校正网络的传递函数为Wapr(s)。则系统的开环传递函数为：

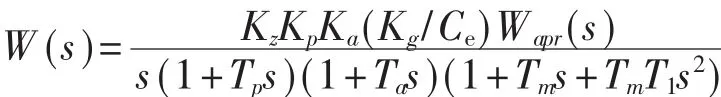
位置随动系统的结构形式，与校正网络的选取有关，它可以决定系统属于哪种类型。为简单起见，可以将系统的传递函数简写为如下形式：

若位置调节器选用比例调节器，即Wapr(s)＝Kobj，则系统函数为W(s)=。这时位置随动系统的结构属于Ⅰ型系统。如果位置调节器采用带有积分环节的调节器，如I，PI或PID调节器时，系统的开环传递函数可以表示成W(s)=，位置随动系统就是一个Ⅱ型系统了。Ⅰ型和Ⅱ型系统是位置随动系统常用的两种典型结构，Ⅰ型系统对于位置输入是无差的，对于加速度输入不能适应，称为一阶无差系统。

S/X波段雷达自身控制系统的反馈电路有两个，反追摆电路和转矩限制电路。反追摆电路用简单测速电桥将伺服电机的反电势反馈回输入端，可视为比例环节；转矩限制电路也可视为比例环节，所以S/X波段雷达应属于Ⅰ型系统。只要知道系统各环节参数，得到系统传递函数，即可选择合适的校正网络提高稳定性。

2 问题解决途径

2.1 动态实时校正

S/X波段雷达在手动和其他雷达同步机直接拖动时是稳定的，在控制计算机产生误差信号输入时出现前面提到的现象。所以应在S/X波段雷达内部接入校正电路或者在控制计算机内实现数字校正网络。这个办法的难点是确定传递函数。由于S/X波段雷达技术说明书只介绍了控制系统工作原理，具体参数值（如伺服电机型号/时间常数）没有列出，所以要想求出系统传递函数，可以用典型信号激励系统并测量输出来求得。

我们知道，衡量位置随动系统稳态性能的唯一指标是稳态误差。稳态误差包括检测元件引起的检测误差、系统结构参数和系统给定输入信号引起的原理误差，以及由负载变化等外部扰动信号引起的扰动误差。其中，检测误差是不可避免的。系统的稳态值Es与输入信号有关，同时也和系统本身的开环传递函数W(s)有关，即和W(s)中所含的积分器个数有关，或者说和系统的结构形式有关，可以进行串/并联、前馈等校正。扰动如风吹天线、放大器飘移、电网电压波动等对Ⅱ型系统影响较弱，所以应将系统校正为Ⅱ型系统。

2.2 提高数传质量

采样频率的选择对系统的性能有重大影响。采样频率低了，不仅会带来较大的误差，而且会使动态品质变坏，甚至可能引起不稳定。假设系统输入信号的最大频率为f，采样频率fs≥2f。但实际上这还是不够的，这只是给出了采样频率的一个下限。采样频率也不能太高，以至于计算机完不成计算，或者伺服机构来不及响应。一般要求为雷达伺服系统带宽的5－10倍，甚至稍大于10倍为宜。或者说大于开环截止频率的10倍以上。之所以要使它大于10倍带宽，其基本出发点在于将本质上是离散时间系统的微机控制系统，近似为连续时间系统，即零阶保持器在这种情况下相位滞后很小，以至可以忽略。

本系统的同步数字转换器采样频率为20次/秒，S/X波段系统闭环带宽为方位角5-12弧度/秒，俯仰角3-10弧度/秒，<2 Hz，可以满足。但引导数据速率不均匀，误码较多，造成影响很大。可以采用光纤传输，以提高数据线路的抗干扰能力。

2.3 控制算法改进

一种理想的控制情形如下：雷达天线以最大加速度启动，达到最大速度向目标位置移动，接近时以最大速度减速并停止在目标位置。要实现这样的控制，可采用分段法（或BangBang控制）：将误差分为大、中、小三个区，在大误差区输出最大控制信号，在中区设减速段，输出相反的控制量减速。在小误差区输出正常控制量。

这种算法需摸清系统的响应特性，必须通过不断的试验改进。

此外可采用模糊神经网络等先进算法，专家控制器、神经网络控制器、模糊控制器是三种典型的智能控制方法。由于专家系统在实际应用中有较多的问题和困难，目前智能控制主要集中在模糊控制、神经网络控制应用上，特别是两者的结合－模糊神经网络。

从上文的分析可知，常规的控制方法主要针对集中参数的线性动态系统，要求对象必须可量化，且各种量化参数的关系能够用微分方程或差分方程来描述，其显著特点是控制系统过分依赖于数学解析的方法和控制系统的精确数学模型。然而，现代系统的复杂性、测量的不准确性以及系统动力学的不确定性，使得采用经典控制理论解决复杂的实际问题时显得无能为力。而智能控制就是将人工智能与控制理论结合起来，完成更高级的控制功能，主要是应用专家系统、模糊控制及神经网络理论等来实现自学习或自组织控制。

3 结语

通过对RCS动态测量系统的深入分析，得到测量雷达传递函数为I型系统。从传递函数矫正、伺服带宽、引导数据传输、控制算法角度讨论了问题的解决途径，经后续使用验证，上述解决方法都是可行有效的。

[1]李连生等.现代雷达伺服控制[M].北京：国防工业出版社,1987.

[2]刘世挺.雷达伺服控制技术的新发展[J].火控雷达技术,2002,31:33-35.