平面度误差评定中离散min-max问题研究与软件设计

林 翔

(福建商业高等专科学校，福建福州350012)

诸如机械加工的零部件，都必然存在实际与理想之间的误差，只有通过检测计算分析，才能评定其误差大小以确定加工成败.此类的形状误差计算，诸如圆度误差、直线度误差、平面度误差等等，一般都涉及到求取离散min-max问题.目前离散min-max问题的计算技术和应用软件，多掌握在欧美及日本等国外几家著名的精密检测仪器研发机构手中，秘而不宣;但从其实际检测的评定结果分析来看，其计算精度亦有局限，平面度方面尤为明显.故笔者从原始概念和定义出发，寻求解决此类min-max问题的新算法，研发高精实用软件，提升评定精度.

1 平面度误差

平面度误差是形状误差的主要内容之一，按《GB/T 1958 －2004》［1］及《JJG 117 －2005》［2］的表述，是指被测物体表面相对于理想平面的变动量.按文献［1－2］要求，平面度误差的计算结果，应该满足最小区域准则，即以理想平面作为基准，使被测物体表面对于基准平面的最大变动量达到最小.

围绕平面度误差的判定准则，专家们研究出了很多评定平面度误差的算法，诸如最小二乘法［3］、最小包容区域法［4］、有序判别法［5］、生物遗传算法［6］等.这些算法的运用，都使平面度误差计算收到不错的计算结果，但由于这些近似算法的先天缺陷，故而计算精度普遍偏低.文献［1］规定，最小包容区域法是最符合最小区域判定准则的，在解决同一个平面度误差计算问题得出不同计算结果时，它是终极评定方法，并以它的结果作为最终仲裁.

归纳这一准则，其要点就是求取2个平行的平面，把被测表面夹在其间，且2个平面之距达到最小.可以这样认为，对于同样一个被测平面，求得的2个包容平面之间距越小，就越接近真值，其算法就是好算法.笔者紧紧围绕平面度误差概念，在目前已经被广泛使用的平面度误差算法的基础上寻求算法，使计算继续进行下去，引导计算结果逐步向最小条件靠拢，从而更精确地评定平面度误差值.

2 探寻新算法

一般情况下，物体的表面形状，是由在表面上测量得到的若干点Pk(xk，yk，zk)(k=1，…，n)来描述的.从最小包容区域法规定可知，平面度误差计算的关键在于求一对平行的平面，它们包容所有测量点Pk(k=1，…，n)，并使平面间距离达到最小.这是一个典型的离散min-max问题.

找到这2个平行平面并不难，可以有很多办法，比如最常见的最小二乘法.不论以何种方法求得基准平面，不妨记其方程为π:ax+by+cz+d=0(如图1所示)，从而求得最小二乘意义下的平面度误差值，如设δ.此误差计算结果是国标［1］认可的，在精度要求不高的情况下已具有实用意义.

图1 基准平面与被测平面示意图

在此基础上，如何对π进行细微的转动，把δ的值降下来，使之向min逼近，是解决min-max问题的焦点.笔者经过观察分析发现，通过有意识地扰动平面π的法方向，使δ值下降成为可能.

设平面π:ax+by+z+d=0(为了讨论方便，此处令c=1.00)是通过最小二乘法拟合得到的初始基准平面，样本点Pk(k=1，…，n)到π的距离为δk(代数值)，其中最大值为δi，最小值为δj，对应的点分别为Pi，Pj，记δi=max(δk)，δj=min(δk)(k=1，…，n)，δj一般情况下为负值;记 δ=| δi- δj|=max(δk)-min(δk)=max(δk)+max(- δk)(k=1，…，n).

Pi在π的投影点为Ai，Pj在π的投影点为Aj，沿着AiPi方向距Ai点ε处(ε是一很小的值)，记作Ai'点;同样沿AjPj方向距Aj点ε处，取Aj'点.设Ai'，Aj'的中点为Q，在平面π上求得点Q'，使直线Q'Q⊥Ai'Aj'.通过这新获得的Ai'，Aj'，Q'3个点，做一个新的平面π'.显然，π与π'的夹角很小，可以把π'看作是将平面π绕直线Q'Q作微小转动以后获得的，从平面方程来看就是π的法向量T(a，b，1)发生微小改变.

设由 Pi，Pj，Ai'，Aj'各点构成的平面为 π1，平面 π 经平面π1剖切，其剖面图如图2所示.易见，Pi到平面π'的距离δi'小于 δi，即小于 max(δk)，Pj到平面 π'的距离 δj'同样下降了，亦即小于max(-δk)，这正是笔者所期盼的:由于将π微小转动生成π'，可能把当前的δ=max(δk)+max(-δk)降下来.

能否令δ值下降，须计算Pk(k=1，…，n)对π'的新平面度误差值δ'并与δ作比较，分如下3种情况分别判断:

1)若δ'＜δ成立，π'取代π，重复上述对π微小扰动、计算、判断过程;

2)若δ'＜δ不成立，缩小ε值并重新求平面π'，重新计算δ'并判断其是否下降;

3)若ε已缩小为非常小的值，达到计算精度要求，则计算终止，此时之δ即最终的平面度误差值.

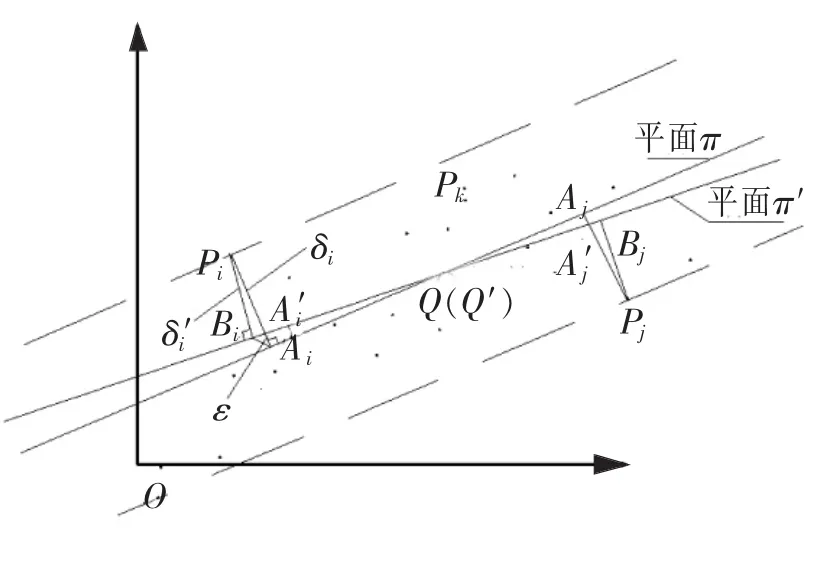
图2 点集Pk与平面π，π′关系图

3 算法的收敛性

对于平面π，π'，设Pi在π的投影为Ai，在π'的投影为Bi，如图2所示.观察△PiAiBi，易见∠PiBiAi为钝角，因钝角的对角边PiAi长度必小于任一邻边，故PiBi＜PiAi成立;同理，对于Pj亦存在1个钝角三角形，Pj至π'的距离比Pj到π的距离小，亦即PjBj＜PjAj成立.

综上，显然有PiBi+PjBj＜PiAi+PjAj成立，即δ'＜δ，这正是所期待的.平面π经微小扰转后，Pk(k=1，…，n)对于新平面π'的δ'值，较之δ一般情况下是单调下降的，这表明平面度误差的计算过程是收敛的，趋于min-max.

算法过程的终止条件为:当ε随着计算过程不断缩小，小到计算要求的精度，经过扰动得到的π'，其δ'=|δi'-δj'|不能再有所下降，即停止计算过程，输出δ.

按上述算法演算至此，平面π即使只作微小扰动，对应的δ不但不减小，反而增大，由此说明，经过一步步单调下降的计算之后，得到的δ极其接近平面度误差真值了，离散min-max问题也得到了解决，所获得的计算结果符合平面度评定中最小条件准则.

4 算法实施

从原则上讲，本算法中初始平面π可以是任意给出的，其收敛过程对其并无任何依赖.但若是初始平面选择适宜，计算过程会收敛得更快.本算法以最小二乘平面作为初始平面.

最小二乘平面的目标方程为

要使D达到最小，只需令

联解3个等式，即可求得初始π的法向量T(a，b，1)及d，平面π的方程也就确定了;再求出Pk(k=1，…，n)相对于平面π的δ=|δi-δj|，δ即最小二乘意义下的初始平面度误差值.

4.2 以初始平面π为基础实施本算法 求得Pk(k=1，…，n)相对于π的正最远点Pi、负最远点Pj，它们在 π 的投影点分别为Ai，Aj，相应的距离为 δi，δj.沿AiPi方向距Ai点 ε 处取点Ai'，沿AjPj方向距Aj点 ε 处取点Aj'，记Ai'Aj'的中点Q，Q在π的投影为Q'，则Q'Q⊥Ai'Aj'.由Ai'，Aj'，Q'3点做平面π'.获取π'之此过程，称为扰动.

对于 π'，参照上述求 δ的过程，求出Pk(k=1，…，n)相对于 π'的2 个正负极值，设为 δl'，δm'，令 δ'=| δl'- δm'|.对于 δ'，δ作如下比较与判断:

1)若δ'＜δ成立，π'取代π，在π基础上求取平面π'，并进行同样的计算和比较;

2)若δ'＜δ不成立，分2种情况分析处理:

①将ε减小，取ε=ε/2重新求出平面π'，求出相应的δ'，返回1);

②如果ε随计算过程已缩小为极小值，满足精度要求，即停止计算，δ即为最终的平面度误值.

4.3 特殊情况处理 算法过程中，若Pk(k=1，…，n)至平面π之正最远点与负最远点不是惟一的，即同属于Pi之类的点有R个，Pj之类的点有S个(R，S≥1)，不妨将R个Pi与S个Pj进行两两配对，那么就产生R*S个组合;对于任何一对Pi，Pj组合，均可进行计算过程，求得相应的平面π'和δ'值.如此求得R*S个δ'值，选出最小者δ'min，令δ'=δ'min，进行1)，2)之比较判断过程，直至满足条件而终止计算，输出δ.

4.4 程序流程图 如图3所示.

被测物体表面的样本点是三维空间的点，且点数较多，因此其算法过程不仅复杂，且计算量大，同时考虑到程序运行完成后要提供具有图示化后处理的功能.因此选择面向对象既长于计算又具有绘图功能的C++作为编程语言.

5 算例及分析

上文从理论上证明本算法收敛于最小区域，得到min-max，满足最小条件，以下通过具体算例加以验证.

图3 程序流程图

文献［7］表3所给的一个算例，平面上5*5=25个测量点，原文以POWELL法计算得到的平面度误差值为8.5 μm;以本文算法程序计算得到的平面度值为8.499 995 3 μm(基准平面法矢:a=-0.000 233，b=0.000 017，c=1.00).

从以上2个算例的计算结果可见，本文算法与原文的算法精度基本一致.

文献［8］给出的算例，平面上测量点有10*10=100个，原文得出的平面度为7.896 321 μm;本文算法计算得出的平面度为5.513 157 8 μm(基准法矢:a=0.000 014，b=0.000 010，c=1.00).

文献［9-10］给出的同一算例，平面上有5*5=25个样本点，其计算出的平面度误差为0.155 2 mm［2］和0.156 6 mm［10］;用本文算法程序进行计算，得出的平面度误差为0.154 869 6 mm(基准法矢:a=-0.026 200，b=-0.054 200，c=1.00).

同样对文献［4-6］所提供的算例进行验算，原文给出的平面度误差值分别为30.25 μm，6.55 μm和8.755 6μm;本文算法程序计算的结果分别为 30.246 612 μm，6.549 999 71 μm 和 6.55 μm.

比较计算结果，本文算法程序计算得出的平面度误差值均小于原文作者所给出的，可见，本文算法在计算精度上有一定的优势.

6 小结

平面度误差值的高精度求取，是典型的离散min-max问题.从计算模型的整定和所寻求的算法原理看，本文算法是围绕平面度误差评定中最小区域展开的.在算法过程中，测量点集Pk(k=1，…，n)对于平面π距离最远发生在哪个点，π就往该点的方位作微小的扰动，保证了计算过程不断地向真值收敛，直至该平面π不能有丝毫扰动为止.本文算法是以最小二乘平面为初始基准平面的，所以算法的整个过程收敛速度很快，实例运算中也说明了这一点.为了计算的方便，尽量将被测平面置于三维坐标系的XOY平面上，尽可能与Z轴垂直.本文算法初始基准平面的选取方法，不局限于最小二乘平面法，与其他算法计算结果相比较，其精度都有一定程度的提高.

［1］中华人民共和国国家质量监督检验检疫总局.GB/T 1958—2004产品几何量技术规范(GPS)形状和位置公差检测规定［S］.北京:中国标准出版社，2004.

［2］中华人民共和国国家质量监督检验检疫总局.JJG 117—2005平板检定规程［S］.北京:中国标准出版社，2005.

［3］张昉.平面度误差的最小二乘法分析［J］.械制造与研究，2002(3):20－22.

［4］吕震宇.一种使用最小包容区域法基于旋转变换求解平面度误差的方法［J］.河北理工学院学报，2000(l):49－59.

［5］张之江，于瀛洁，张善钟.平面度误差最小区域新算法—有序判别法［J］.计量学报，1998(1):16－22.

［6］温秀兰，宋爱国.基于实数编码的改进遗传算法及在平面度误差评定中的应用［J］.计量学报，2003(2):10－13.

［7］彭祖行.形状误差的优化算法［J］.计量学报，1992(4):7－12.

［8］蔡改贫，朱同发.单基准给定方向轴线对平面倾斜度误差的评定［J］.南方冶金学院学报，1998(3):179－183.

［9］温秀兰，赵茜.基于进化策略的平面度误差评定［J］.仪器仪表学报，2007(5):66－70.

［10］薛小兰.遗传算法及其在平面度误差评定中的应用［J］.晋中学院学报，2009(3):12－14.