基于集成分量的基因微阵列数据分类方法的研究
宋红胜,孔 薇
(上海海事大学 信息工程学院,上海 201306)
自Golub等于1999年开创了基于基因表达谱的肿瘤分类领域以来,研究者已经提出许多基于基因表达谱的分类方法,这一领域也迅速成为生物信息学的主要研究方向之一,如,人 工 神 经 网 络 (Artificial Neural Network,ANN)、 贝 叶 斯(Bayesian)、决策树(Decision Tree)和支持向量机机(Supporting Vector Machine,SVM)等经典的分类器。由于微阵列数据集高维、小样本和高噪声等特点,对建立高精度的分类模型提出了挑战,而且基于实验表明不同的分类器对同一数据集分类效果不同,即使对同一数据集运用同一种分类器分析,随着提取特征基因的不同,实验结果会有很大差别。因此,为了提高分类模型的分类性能、稳定性以及泛化能力,研究人员把很多分类器集成起来,并采用某种决策策略对多个分类器的分类结果进行判定以决定最终的分类结果。
自从Sebestyen于1962年在其书中提出层叠多分类器集成系统的设计思路以来,集成分类系统的研究直到90年代才受到重视,许多学者也纷纷加入对其的研究,如Hansen和Salamon通过投票法将所有的神经网络结合起来解决问题,发现其性能比最好的个体神经网络的性能还好[1];Schapire也在自己的论文中证明了通过构建多分类器集成系统,弱分类器可以与强分类器等价[2];并且研究者也设计不少优秀的集成系统算法,如 Bagging、Boosting、AdaBoost、Random Forest、Rotation Forest、Wagging和Arcing等,这些方法已经被广泛应用于生物信息学等各个领域中。
从不同的角度可以得到不同的集成分类器方法,由于这些方法所选择的分类特征不同,因此分类器本身就具有差异性,在独立成分分析集成算法中独立分量的选择的标准有很多,在Liu提出基于独立分量集成方法的论文中,是利用遗传算法提取独立分量[3],而本文中对独立分量系数矩阵A的hinton图进行生物学分析比较,选取独立分量。
为了得到差异性就大的分类器,文中选取不同方法进行特征基因选择,并对选取的特征基因集进行ICA变换,以获得一组独立分量集,随之根据矩阵A选择出一组较优的独立分量集。为了比较算法,本文还构建基于PCA和NMF的集成系统,该算法框架与集成独立分量选择系统相同。
1 基于集成分量的分类系统设计
分类器集成比单个分类器更有效的充分必要条件不仅是集成中的分类器的精确性而且是其错误差异性,因此,对于初始数据的特征提取与选择方法是一个重要环节,它的优劣将极大影响着分类器的设计和性能。
1.1 基于小波包变换的去噪处理
原始DNA微阵列数据不可避免包括大量的实验随机误差和系统误差,所以为了反映生物本质的分类结果,在进行基因表达谱分类之前必须进行去噪处理。文中分类系统中选用小波包对数据进行去噪[4]。小波包变换(Wavelet Packet Transform,WPT)的概念是由Wickethauser M V和Cnifinan R R等人在小波变换的基础上进一步提出来的,小波包分析属于线性时频分析法,它具有良好的视频定位特性以及对信号的自适应能力,因而能够对各种时变信号进行有效的分解。
1.2 特征基因初选
特征基因初选可以基于统计分析来选取相关基因,即对原始基因集合基于某种记分准则对基因进行排序,基因分值大小反映了基因的重要程度和分类能力,设定一定的阈值选取对基因表达谱分类具有较大贡献的信息基因。常用的基因特征记分准则有:
2)修订的特征记分准则(Revised Feature Score Criterion,RFSC):
3)Fisher判别(Fisher Discriminant Ratio,FDR):
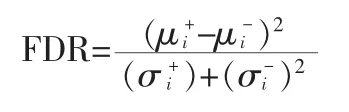
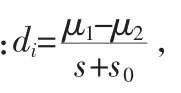
1.3 集成分量的选择方法
在的初选基因集合后,需要对其进一步特征提取和选择,常用的特征提取方法主分量(Principal Component Analysis,PCA)、因子分析(Factor Analysis,FA)、独立分量分析(Indepen-Dent Component Analysis,ICA)、非负矩阵分解(Non-gegative Matrix Factorization,NMF)和线性判别分析(Linear Discriminant analysis,LDA)等,笔者使用PCA、NMF和 ICA对初选基因集进行变换,以获得分量,接着运用下面方法从该分量集选择出一组较优的分量子集,每个分量子集分别用于基分类器的训练,从而获得一组基分类器。
1.3.1 基于PCA的分量选择
PCA作为多元统计分析中应用广泛的数据降维方法,是一种基于目标统计特性的最优正交变换,其目的是寻找任意统计分别的数据集合中的主要分量的子集[6]。选择主分量的方法如下:
1)对矩阵X中的数据进行标准化处理(即使均值为0,方差为1),所得到的标准化后的矩阵为X1,计算矩阵X1的相关系数矩阵R;
3)根据特征值,选择ω个主分量,从而达到特征提取的目的。
1.3.2 基于NMF的分量选择
NMF是由Lee和Seung于1999年在《Nature》上提出的[7],NMF是在矩阵中所有元素均为非负数约束条件之下的矩阵分解方法,它的基本思想是将一个非负矩阵近似分解为两个非负矩阵的乘积,来反映数据潜在的线性结构,数学描述为:对于非负矩阵 Vm×n,近似分解为非负矩阵 Wm×k与 Hk×n的乘积,即:V≈WH,其中k已知或未知,W为基矩阵,H为系数矩阵,且这两个矩阵必须都是非负的。从生物意义上看,经过非负分解所得W的每一列可以对应着某一生物过程,矩阵V的每一项可以看成对应的基因在各生物过程中表达模式的加权和,权向量即为H的对应列,H矩阵之所以能区分样本的不同属性是由于集合基因在每一个样本中表达值有差异。因此,可根据W矩阵提取分量,具体方法如下[8]:
1)确定k值,再运用NMF算法对基因表达数据进行分解,k值由最大的共表型相关系数对应的k值来确定;
2)将W矩阵的各个列分别两两求商,并用一个矩阵S保存结果,将S矩阵各列的值按照从大到小的顺序进行排列,值越大的基因表明它在正常组织与疾病组织中差异表达越明显;
3)设定合适的阈值,提取一定数量的显著差异表达基因,组成子基因集。
1.3.3 基于ICA的分量选择
ICA的概念是由法国学者Jutten和Herault J等人于1986年提出[9],最初是用来解决盲源信号分离(BSS)问题,其基本思想是在特种空间上寻找最能使的数据互相独立的方向。对应的混合与分离模型可用以下公式表示:
X=AS;U=S=A-1X=WX, 其中 Xn×p是基因表达谱矩阵,Sn×p称为n个独立成分 (Independent Component,IC), 表示源矩阵,即每一行变量即为相应的独立分量,而An×n为混合矩阵,可以描述为基因表达数据集X是一个独立分量集S与一个未知的线性混合矩阵A的线性混合。混合矩阵A中各列的值是一个值得研究的问题,而且可能揭示一些隐含的生物特征,文中将对混合矩阵A从生物意义上来分析,提出一种基于混合矩阵A的Hinton图 (一种对矩阵权重进行可视化的方法)选择独立分量子集的方法。从生物意义角度来看,经ICA变换所得的S矩阵每一行为一个独立成分,每一列表示一个样本,X每列为一个样本,也可看成是一组信息基因(独立成分)的线性组合,而混合矩阵A的每列的值确定这种线性组合的系数。因此,A矩阵之所以能区分样本的不同属性是由于不同的独立成分在每个样本中表达值不同,即线性组合时系数的不同,因此,认为由于基因对个独立成分的数值上贡献的不同,导致了独立成分在不同的样本中表达值不同。对独立成分贡献有明显差异的基因,被认为是与疾病发生有密切关系的差异表达基因。提取独立分量得具体方法如下:
从表7可以看出,锡石多金属硫化矿主要矿石矿物的吸波能力存在显著差异,其中,脆硫锑铅矿的吸波能力最强,其次是黄铁矿,再次是锡石,闪锌矿和脉石矿物的吸波能力最差。因此,锡石多金属硫化矿主要矿石矿物的吸波能力差异奠定了锡石多金属硫化矿的微波选择性加热的基础。
1)对初选的基因表达谱数据进行初始值不同的ICA变换;
2)根据混合矩阵A的Hinton图选取独立分量;
3)设定合适阈值,提取特征基因。
2 基于集成分量的分类系统模型
集成分类器比单个优秀的分类器更加有效,主要原因是组成集成分类器之间的差异性,即它们产生的错误分布在不同的数据空间中,一个分类器产生的错误能够被集成系统中其他分类器补偿,集成才有效[10],因此,可以先生成大量基分类器,然后选择其中部分基分类器集成。图1为基于集成分量的分类系统流程图,首先对训练集预处理后,按某种准则对基因排序,进行降维,随后对初选集进行PCA、NMF或ICA变换,使用上文的方法选取分量子集训练基分类器。为了增大基分类器之间的差异性,还构建了混合集成分量分类系统,此系统和集成分量系统主要差别是对同一训练集,采用不同的变换方法,将生成不同的初选集,然后对这些初选集进行变换,这样得到的基分类器会有很大的差异度,直接集成这些分类器可以构造一个稳定的集成分类系统,具体流程如图2所示。
3 实验结果与分析
3.1 实验数据
文中实验使用GEO数据库上两个基因表达谱数据:GDS 2519(早期帕金森症数据集)和GDS2771(肺癌数据集),对于这些数据集中,所有样本都预先被划分为训练样本和测试样本,文中每次随机将数据集划分为2:1的比例,其中1/3样本作为测试数据,另外2/3样本作为训练集合。
3.2 实验结果比较分析
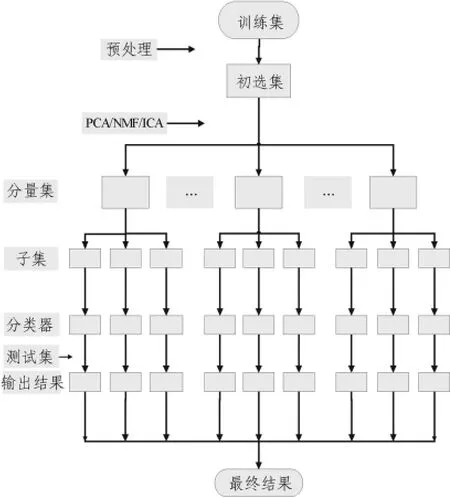
图1 集成分类系统Fig.1 Ensemble classification system
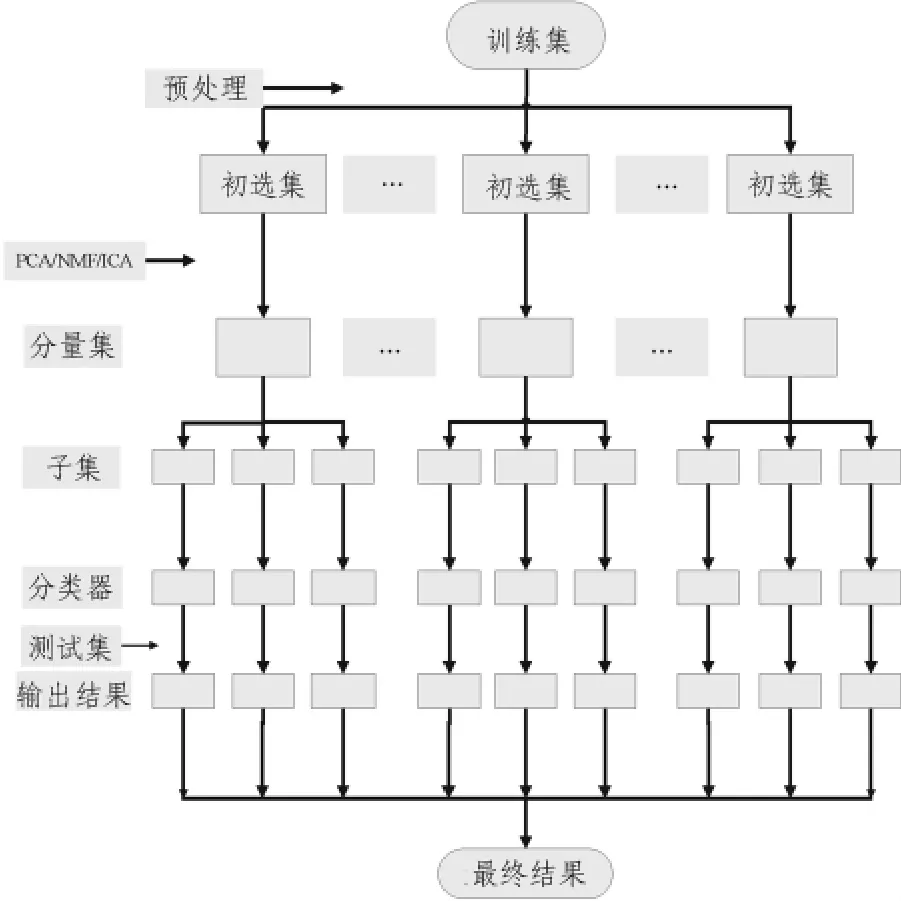
图2 混合集成分类系统Fig.2 Mix-ensemble classification system
1)对于单个分类器,集成分类的方法获得的分类准确率更高,对于不同的数据集,不同的集成分量方法得到的结果会有所差异,如在表中,数据集GDS2519的EICA方法比ENMF和EPCA效果更好,但在数据集GDS2771中情况有所不同,如在对GDS2771数据进行FDR和RFSC特征提取后的集成结果显示,ENMF比EICA准确率更高。如果将EPCA与EICA的结果相比,显然EICA在两个数据集上都获得了明显优于EPCA的结果,其原因是,相对于PCA,ICA更适合基因表达谱的分析。
2)对同一数据,不同的特征提取方法得到的结果也有所不同,在单个分类系统中,SAM方法都获得相对较高的结果,在同一种集成分量的方法中,SAM方法也获得了相对较高的结果。
3)对于混合集成分类系统,可能其分类的准确率不一定高于集成分量系统,但比较它们的标准差,我们可以发现,单个分类器的准确率的值浮动很大,集成分量系统的值浮动较小,混合集成系统的准确率浮动最小,这是由于在集成分量系统中,训练基分类器的初选集是由同一种方法变换得到的,基分类器之间的差异性并不是很大,而混合集成分量系统中的训练基分类器的初选集是由不同准则变换得到的,由此获得的分量子集差别较大,因此,训练得到的基分类器差别也较大,这样在准确率方面,相互之间可以弥补,从而构造一个稳健的集成系统。
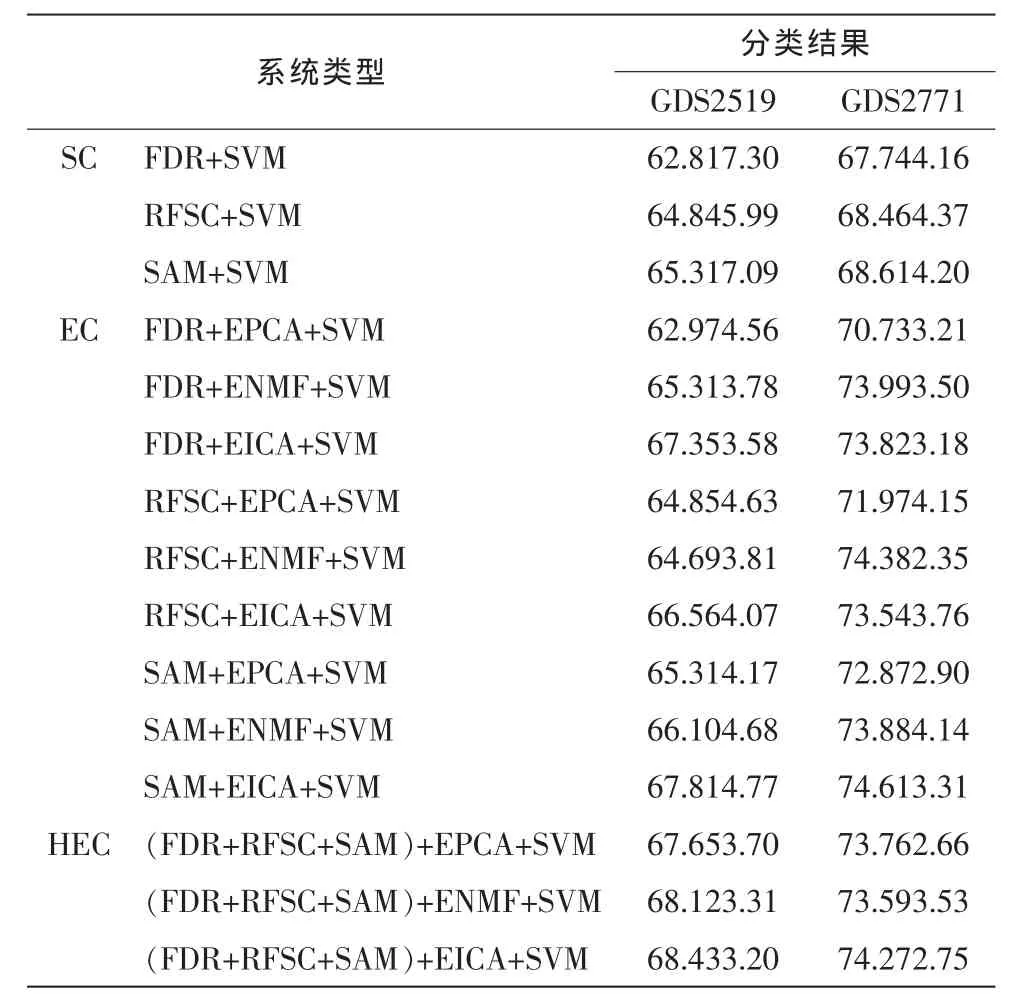
表1 分类结果Tab.1 Results of classifiction
4 结束语
实验数据表明集成分量系统可以提高微阵列数据在分类问题中的准确性,其分类准确性优于单个分类器。文中构建的不同种类集成分量系统具备一定的可行性,对于筛选差异表达基因的方法还可以尝试更多有效的方法,对于混合集成分量系统,如何构造一个准确率高而且稳健的集成系统,则有待进一步的深入探讨。
[1]Hansen L K,Salamon P.Nenral network ensembles[J].IEEE Transactions on Pattern Analysis and Machine Inteligence.1990,12(10):993-1001.
[2]Schapire R E.The strength of weak learnability[J].Machine Learning.1990,5(2):197-227.
[3]LIU Kun-hong,LI Bo,ZHANG Jun,et al.Ensemble component selection for improving ICA based microarray data prediction model[J].Pattern Recognition,2009(42):1274-1283.
[4]YANG Yong-ming,LU Cheng-hong.The application of wavelet packet analysis in getting rid of noise in one-way and twoways signals[J].Xi’an Univ.of Arch.&Tech,2004(36):3.
[5]Tusher V G,Tibshirani R,Chu G.Significance analysis of microarrys applied to the ionizing radiation response[J].PNAS,2001,98(9):5116-5121.
[6]YOU Wen-jie,JI Guo-li,YUAN Ming-shun.Feature reduction on high-dimensional small-sample data[J].Computer Engineering and Applications,2009,45(36):165-169.
[7]Lee D D,Seung H S.Learning the parts of objects by nonnegative matrix factorization[J].Nature,1999(401):788.
[8]杜芳,饶妮妮.基于非负矩阵因子分解算法提取胃癌差异表达基因[EB/OL].(2009-04-08).http://www.paper edu.cn/index.php/default/releasepaper/comment_paper/200904-253.
[9]Herault J,Jutten C.Space or time adaptive signal processing by neural network models[C]//AIP Conference Proceedinys,1986(151):206-211.
[10]LIU K H,HUANG D S,ZHANG J.Microarraydata prediction by evolutionary classifier ensemble system[C]//IEEE Congress on Evolutionary Computation (CEC),Singapore,2007:3215-3220.

