一维单通道可调谐光子晶体窄带滤波特性研究

王玉玲，吴春梅，姜 赫

(大庆师范学院 物理与电气信息工程学院，黑龙江 大庆 163712)

0 引言

光子晶体是一种介电常数按一定周期发生变化的人工微结构材料, 其概念是由 Yabl- onovitch[1]和John[2]在 1987 年各自独立提出来的, 它来源于Maxwell方程和Schrodinger 方程以及光子和电子的类比。类似半导体材料存在电子带隙，光子晶体中也存在光子带隙，这就意味着光子晶体有很多方面的应用[3-5]。同样类似于半导体材料，在光子晶体中引入杂质层，在光子晶体中也会出现缺陷模和缺陷态，据此引入杂质层的光子晶体可用来制作激光器、发光二极管、滤波器等。对于引入杂质层的光子晶体的特性研究，以前主要集中于晶体参数对滤波特性的影响。目前学者们开始关注可调谐光子晶体的特性研究，在光子晶体中引入各种智能材料，利用材料本身的非线性光学效应，电光效应，热光效应等实现光子禁带和透过带的可调的特性。同时许震宇、刘启能等人[6-7]研究了在光子晶体中引入空气层，利用外加微机械力改变空气层厚度达到调节带结构的目的，这种方法具有非破坏性的连续可调和调节速度快的优点。但是目前对单通道空气层厚度和中心波长对窄透过带位置、调谐范围、透过带峰值没有详细研究。本文利用传输矩阵方法研究了含空气缺陷层的周期性光子晶体带隙特性，并详细分析了缺陷层厚度和中心波长对带隙中窄透过带的位置和透过带峰值的影响。

1 理论模型

研究的一维含空气缺陷层的光子晶体，其结构如图1所示，周期性材料为A和B，中间为外加微机械结构可调厚度的空气层C，它们对应介质层的折射率和厚度分别为(na,a)， (nb,b)， (nc,c)。设光从左向右垂直入射，此晶体的基本结构为(AB)NC(AB)M。为方便计算我们设左侧由介质A、B构成的特征矩阵为MN=MaMb…MaMb ，右侧为MM，故整个结构的特征矩阵为M=MNMCMM。其中单层介质的特征矩阵为：

(1)

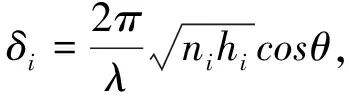
对于一维光子晶体，当膜层包含n层时，整个膜系的特征矩阵M可由各个膜系的特征矩阵Mi的连乘积求得。

(2)

通过M可得出膜层的反射系数和透射系数,反射率和透射率为：

(3)

反射率R=|r|2

(4)

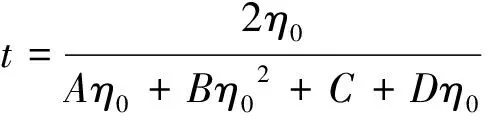
(5)

透射率T=|t|2

(6)

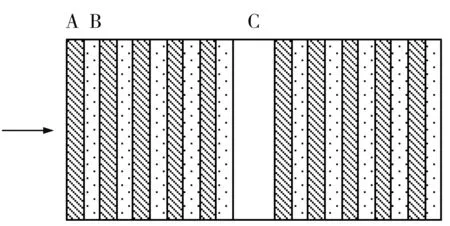
图1 含空气缺陷层的一维光子晶体模型

2 数值模拟和结果分析

设所研究介质两端为空气层，入射波为平面TE波(此时TM模式相同),且垂直于介质表面入射(θ=0)，结构A选为硫化锌(nA=2.38),B选硫化镁(nB=1.38),C为空气层(nC=1.0)，介质层的光学厚度nihi为300nm。空气层两侧的周期性结构的周期数都为5。

利用传输矩阵方法，用Matlab编程软件将上面的参数带入公式进行模拟计算,当空气层光学厚度与周期性介质厚度相同时，其带隙结构如图2所示。该结构在1000～1500nm处出现光子禁带，由于空气缺陷层使光子晶体原有的对称性被破坏，在光子晶体的禁带中出现频率极窄的缺陷态，即在禁带中1200nm处出现了一个超窄透过带，窄透过带局部放大图形如图2b所示，其半高宽度为2.4nm。改窄透过带可以用来制作光子晶体窄带滤波器。

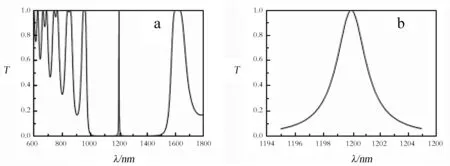
图2 含空气缺陷层的一维光子晶体透射谱

利用微机械装置微调空气层两端的周期性结构，改变空气层的厚度，可以达到调谐窄透过带的目的。如图3所示，窄透过带随空气层厚度的增大而向红外方向移动。为详细观察窄透过带随空气层厚度变化关系，我们在图3b中详细画出了窄透过厚度在50～550nm范围内的变化情况。由图可以看到透过带的频率随空气层的厚度的增加近线性的向地频移动，其可调范围是360nm,而其透过带的峰值在0.87～1.00内变化，其平均值大于0.98，所以利用该结构可以快速，无损重复的调节窄透过带的频率位置，进而可以制作可调光子晶体窄带滤波器。

图3 空气缺陷层厚度与窄透过带位置和透过带峰值关系图

由于介质的光学厚度nihi和中心波长λ0之间存在nihi=λ0/4的关系，我们可以通过改变介质层厚度来改变中心波长，计算发现透过带的调谐范围和中心波长间存在密切关系，当中心波长变为1800nm时，窄透过带的可调范围增大到469nm。调谐范围随中心波长的增大而增大。

3 结语

含空气缺陷层的光子晶体结构，空气层厚度可通过外加微机械力调节两侧周期性结构距离来调节，从而达到调节禁带中窄透过带的目的。通过计算得到以下结论：①窄透过带的位置随空气层厚度的增加近线性的向红外方向移动，空气层在50～550nm之间厚度连续变化，窄透过带调节范围为360nm ；②透过带峰值在调节范围内平均值大于0.98；③调节范围随中心波长的增大而增大。以上结论对设计和制作光子晶体可调窄带滤波器具有一定的理论指导意义。

[参考文献]

[1] Yablonovitch E. Inhibited Spontaneous Emission inSolid2State Physics and Electronic[J]. Phys Rev Lett, 1987, 58:2059.

[2] Johns. Strong location of photon in certain disordered dielectric super lattices[J]. Phys Rev Lett, 1987, 58:2486-2489.

[3] Hu Gufeng, Chen, Daru，Jiang Xiaogang. Side-hole two-core micro-structured optical fiber for hydrostatic pressure sensing[J]. Applied Optics,2012, 51(20):4867-4872.

[4] Soh Hyun-jun, Yoo Jeonghoon, Kim Daekeun. Optical design of the light absorbing layer in thin film silicon solar cells[J]. Solar Engergy, 2012, 86: 2095-2105.

[5] Nojima S.， Usuki M. Yawata. Fano resonances for localized intrinsic defects in finite-sized photonic crystals[J]. Physical Review A, 2012, 85(6):063818.

[6] Xu Zhenyu. One-Dimensional Mechanically Tunable Photonic Crystal[J]. Journal of Tong Ji University:Natural Science，2006,34(7):978-980.

[7] Liu Qineng. Theoretical study on photonic crystal tunable filter with multiple channels[J]. Journal of Applied Optics，2008, 29(4):639-643.