利用分形理论评价潜山裂缝型油藏油井产量变化特征

王月杰 童凯军 程大勇 张宏友 程奇

(中海石油(中国)有限公司天津分公司渤海油田勘探开发研究院)

利用分形理论评价潜山裂缝型油藏油井产量变化特征

王月杰 童凯军 程大勇 张宏友 程奇

(中海石油(中国)有限公司天津分公司渤海油田勘探开发研究院)

以渤海海域JZ25-1S油田为例，利用分形理论评价了潜山裂缝型油藏油井产量的时间序列变化特征，建立了分形维数与产出流体类型、生产井型及不同工作制度的关系，结果表明:油井产量具有很好的分形特征，分形维数与产出流体类型基本无关;同一井组内，水平井生产的分形维数高于定向井;同一口井不同工作制度生产对应油井产量的分形维数不同，随着油嘴或泵频率逐步增大，对应的分形维数逐步减小。通过研究油井产量的分形维数可以用间接表征裂缝型油藏储层裂缝发育程度，而且油井产量的分形维数越大，储层的裂缝越发育，油井采油指数递减幅度也越小。

潜山裂缝型油藏油井产量时间序列分形维数变化特征JZ25-1S油田

从Arps开始［1］，对油气田开发规律的研究多集中在油气田开发产量递减规律上，在时间尺度上属于宏观大尺度，而对于油田或油井产量变化所蕴含的内在规律研究较少。近年来，分形几何学理论的引入为定量描述自然界中不规则及复杂现象提供了有效工具［2］，在油田开发中也得到了一些应用［3-5］，包括用分形理论来解释试井问题、描述裂缝和孔洞结构及描述两相流等，并且大量研究已表明原生孔隙介质、裂缝和溶蚀孔洞在储集层内部的分布具有分形特征，但目前关于间接反映储集层性能的动态响应——油井产量是否也具有分形特征的研究还很少见。

JZ25-1S油田太古界潜山油藏是渤海海域近年来投入开发的第一个大型潜山油藏，油藏构造顶部风化严重，主要受区域构造作用影响以及包括变质作用、物理风化作用、化学淋滤及矿物充填作用等多种因素在内的交替影响，形成了复杂的储集空间和非均质性较强的储层;区内油井产量的大小受很多因素影响，且影响关系错综复杂，表现为既非确定的，也非完全随机的一种模糊系统状态。本文采用分形几何学方法分析了JZ25-1S潜山裂缝型油藏油井产量时间序列的内在特征，计算了不同产出流体类型、不同井型及不同生产工作制度所对应的分形维数，研究了潜山裂缝型油藏油井产量的分形演化规律，并结合研究区地质特征进一步探讨了油井产量分形维数所代表的地质意义。

1时间序列分形特征分析基本原理

油井产量随时间的分布曲线可理解为一个产量数据的时间序列。对于一个特定的油井产量时间序列，通常可采用参数模型进行分析，如Arps递减模型、灰色模型和其他非线性模型等［6-7］。本文为分析油井产量的时序特征，采用了分形几何学的方法。

在裂缝型油藏动、静态相关参数的研究中，分形是指一个分形体内部任何部分参数变化的复杂程度与整体或其他部分都是相似的，定量描述这种自相似的参数是分形维数。目前计算分形维数最常用的方法是重标极差法［8-9］。采用重标极差法求取分形维数的计算公式如下:

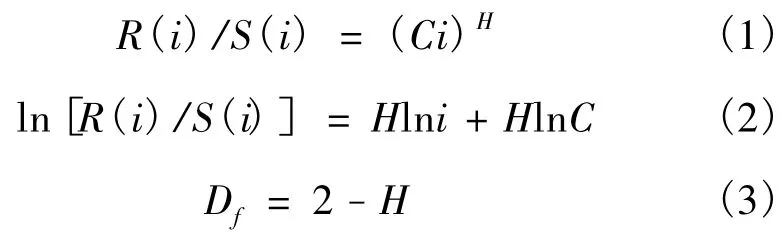
式(1)～(3)中:R(i)为极差;S(i)为标准差;C为常数;i为数据个数，取值为1，2，…，n;H为Hurst指数;Df为分形维数。

2 JZ25-1S潜山裂缝型油藏油井产量的时间序列变化特征

2.1 油井产量时间序列曲线预处理

在生产过程中，油井产量数据的计量往往不可避免地存在各种噪音信号的干扰，例如测试工具、人工计量等，结果使得生产曲线存在很大的跳跃性。因此，在应用生产动态曲线之前有必要对油井产量时间序列曲线进行预处理，消除存在于测量数据中的噪音信号。对于噪声一般表现出的高频特性，在信号小波变换域中，噪声信号对应的离散小波变换系数一般分布在较高精度的系数上，而且多数情况下这些系数幅度都较小。为此，在小波分析的基础上，将小波去噪的方法引入到生产动态分析中，获得了较好的应用效果(图1)。

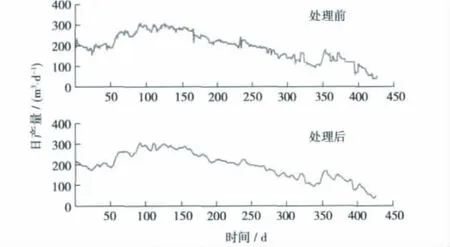
图1 JZ25-1S油田A35井产油量去噪前后对比变化曲线

2.2 分形维数与流体类型的关系

本次研究共获得区内9口油井的生产动态历史数据。利用上述分形维数计算方法，基于Matlab软件分别计算了这9口油井产量的分形维数。例如A35定向井位于潜山构造低部位，生产段距离油水界面很近，投产后即油水同产，6.35 mm油嘴生产，油压控制在2.5 MPa，由于天然能量不足，日产量出现振荡起伏的下降趋势。同样，区内其他8口生产井的产量变化特征与A35井相类似，这表明JZ25-1S潜山裂缝型油藏油井产量的不稳定性具有普遍性，由此可借助R/S方法对其生产动态的时序特征进行描述。图2为A35井不同产液类型分形处理结果。从图2可以看出，lg［R(i)/S(i)］～lg(i/2)具有很好的线性关系，表明油井产量时间序列具有分形特征。采用最小二乘法拟合得到A35井日产油量、日产水量、日产液量对应的Hurst指数分别为0.982 2、0.992 3、0.981 6，对应的分形维数分别为1.017 8、1.007 7和1.018 4(平均值为1.014 6)，与分形维数平均值之间的相对误差分别为0.32%、－0.68%和0.37%。相对误差都很小，可以认为具有相似的分形维数。由此可见，油井的日产油、水、液量具有基本一致的分形维数，可以认为油井产量分形维数与油井产出的流体类型基本无关。

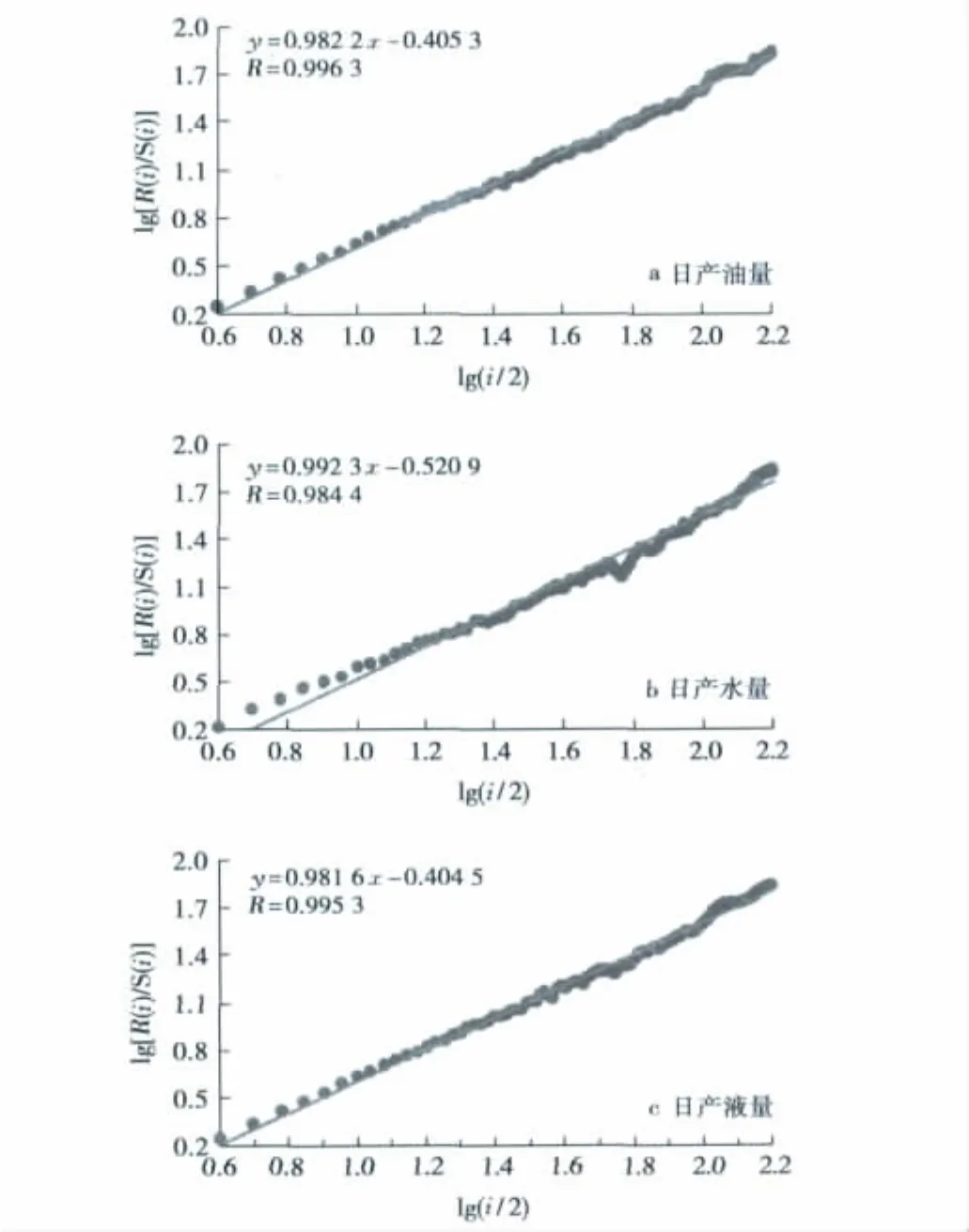
图2 JZ25-1S油田A35井不同产液类型Hurst指数计算结果

2.3 分形维数与生产井型的关系

图3为研究区内A30H、A31井日产油量随时间变化曲线。其中，A30H井为水平井，A31井为定向直井，且2口井属于同一井组，大部分时间内均为自然生产，人为干预因素较少。分别对这2口井的日产油量变化曲线进行分形处理，结果见图4。由图4可见，A30H、A31井的lg［R(i)/S(i)］～lg(i/2)都具有很好的线性关系，对应的Hurst指数分别为0.907 0、0.988 6，对应的分形维数分别为1.093 0、1.011 4。可见，水平井对应的分形维数大于定向直井对应的分形维数，可以认为油井产量分形维数与生产井型有关。

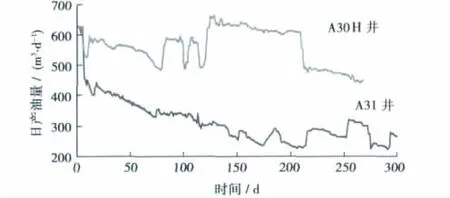
图3 JZ25-1S油田不同生产井型油井日产油量随时间变化曲线

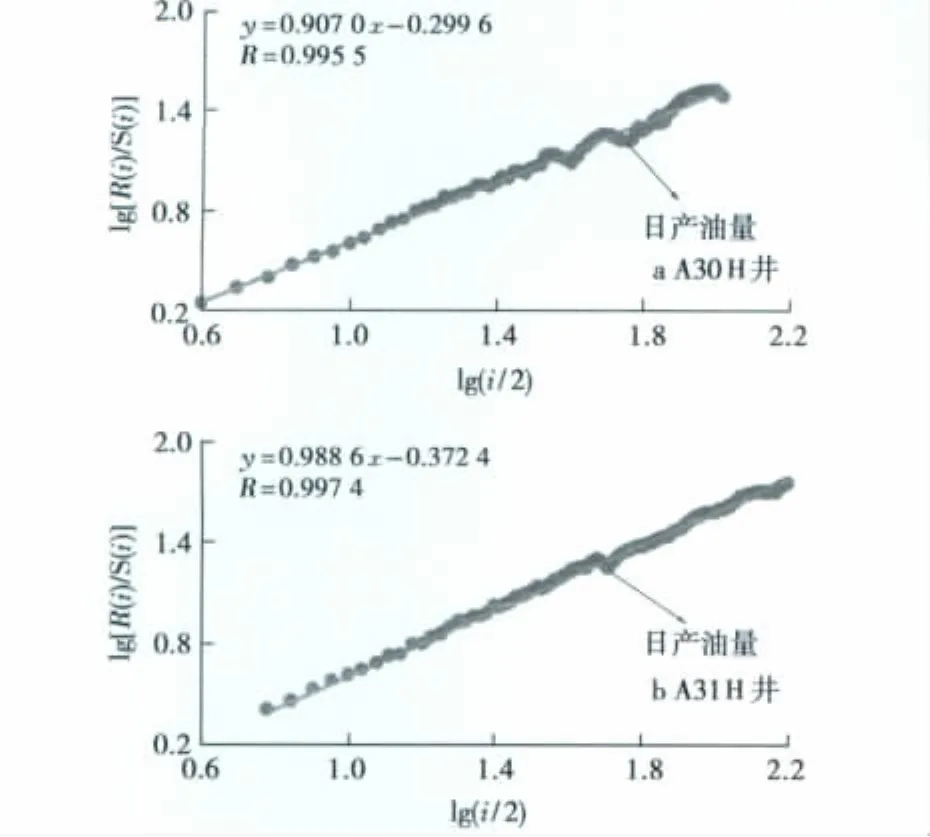
图4 JZ25-1S油田不同生产井型油井日产油量时间序列特征Hurst指数计算结果

2.4 分形维数与生产工作制度的关系

图5 JZ25-1S油田A30H井不同工作制度下生产动态参数随时间变化曲线

以A30H井为例，分析5种生产工作制度下油井日产油量及井底流压的变化规律，如图5所示，其中工作制度Ⅰ～Ⅳ根据油嘴大小及泵频率值划分(工作制度Ⅰ为13.8 mm油嘴、40 Hz泵频率，工作制度Ⅱ为15.88 mm油嘴、45 Hz泵频率，工作制度Ⅲ为16.27 mm油嘴、50 Hz泵频率，工作制度Ⅳ为14.35 mm油嘴、45 Hz泵频率)，工作制度Ⅴ不考虑油嘴及泵频率的差异。对5种工作制度下A30H井日产油量及井底流压数据分别进行分形处理后，绘制lg［R(i)/S(i)］～lg(i/2)关系图，拟合得到该井不同工作制度下日产油量及井底流压分形维数(表1、2)。从表1、2可以看出，随着油嘴或泵频率的增大，对应的油井日产油量及井底流压分形维数有逐渐降低的趋势，而且不考虑油嘴及泵频率的差异生产所对应的油井日产油量及井底流压分形维数最小，说明分形维数能够反映油井工作制度的变化特征。分析认为:对于特定的油井而言，其生产潜力是基本确定的，那么采用小油嘴或较小的泵频率生产时，其生产的稳定性及生产潜力一般比大油嘴或大泵频率生产时要好，而且频繁改变工作制度会加剧油井生产的不稳定性。因此，分形维数的物理意义表征了油井生产的稳定性或其生产潜力的大小，对于特定生产油井而言，当油井生产越稳定、生产潜力越大时，其对应的分形维数也越大。

表1 JZ25-1S油田A30H井不同工作制度下日产油量的分形维数计算统计表

表2 JZ25-1S油田A30H井不同工作制度下井底流压的分形维数计算统计表

3油井产量分形维数表征地质意义

图6为研究区油井采油指数变化幅度与分形维数拟合曲线，二者之间遵循较好的线性关系。油井采油指数变化幅度越小，分形维数越大，反之亦然。从地质角度分析，裂缝型油藏油井产量的变化特征是由储集层内裂缝发育程度决定的，裂缝越发育，供油能力越强，生产越稳定，对应油井采油指数递减幅度越小，分形维数也越大。因此，通过研究油井产量的分形维数可以间接表征裂缝型油藏储层的裂缝发育程度。

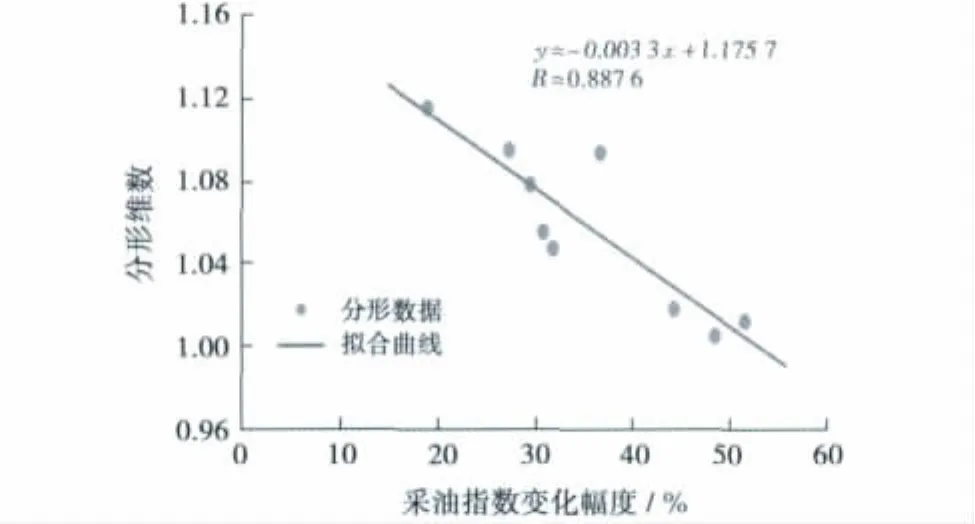
图6 JZ25-1S油田采油指数变化幅度与分形维数拟合曲线

运用克里金插值技术对全区油井产量的分形维数绘制了平面等值线图(图7)。研究区可明显划分出高、低分形维数值2个区域，其中以A25H井为中心的A25H-A18H-A17H为分形维数高值区，该区分形维数变化主要沿构造高部位分布，这与潜山高点控制储层分布及构造高部位裂缝发育的地质认识吻合，油井具有单井产能高、产量递减慢、生产潜力大的特点;而以A35井为中心的A31-A35-7为分形维数低值区，该区分形维数变化主要沿构造低部位分布，该区储层裂缝发育程度低，油井具有初期产能低、产量递减幅度大的特点。

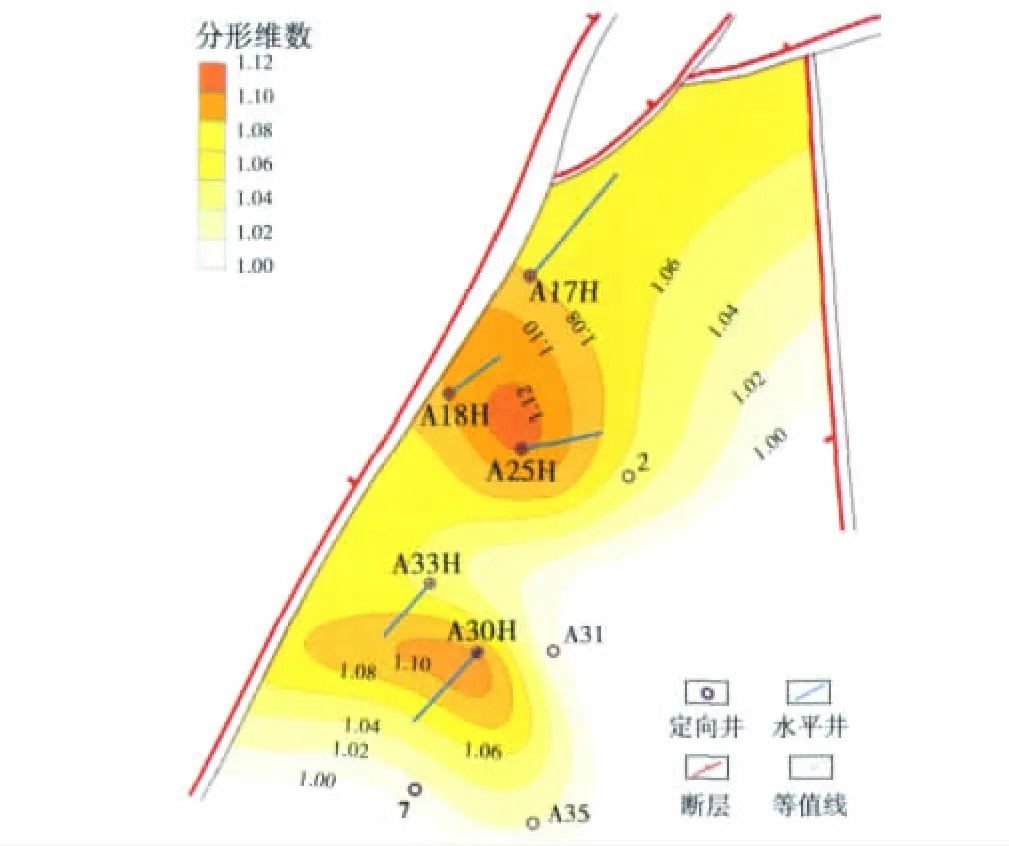
图7 JZ25-1S油田分形维数等值线图

4结论

(1)以JZ25-1S油田为例，研究了潜山裂缝型油藏油井产量的时间序列变化特征，结果表明潜山裂缝型储集层油井产量具有较好的分形特征，分形维数与产出流体类型无关，同一井组内水平井生产比定向井生产分形维数大，油嘴或泵频率增大会导致分形维数变小。

(2)通过研究油井产量的分形维数可以间接表征裂缝型油藏储层裂缝发育程度，而且油井产量的分形维数越大储层裂缝发育越高，油井采油指数递减幅度也越小。

［1］ARPS J J．Analysis of the decline curves［J］．Trans．AIME，1945，160:228-247．

［2］朱晓华，闾国年．地质灾害中的分形研究进展［J］．中国地质灾害与防治学报，2000，11(1):11-14．

［3］唐玮，唐仁琪，白喜俊．分形理论在油层物理学中的应用［J］．石油学报，2008，29(1):93-96．

［4］李凡华，刘慈群，宋付权．分形在油气田开发中的应用［J］．力学进展，1998，28(1):101-110．

［5］JULLO SS．North Vickers Eastwaterflood performance prediction with fractal geostatistics［A］．SPE 21897，1993．

［6］吴怀宇．时间序列分析与综合［M］．武汉:武汉大学出版社，2004:25-27．

［7］谢焱石，谭凯旋．断裂构造的分形研究及其地质应用［J］．地质地球化学，2002，30(1):71-77．

［8］王志国，杨文哲，宋永臣，等．油气集输过程产量重标度极差分

析方法［J］．石油勘探与开发，2010，44(1):618-622．

［9］贺可强，孙琳娜，王思敬，等．滑坡位移分形参数Hurst指数及其在堆积层滑坡预报中的应用［J］．岩石力学与工程，2009，28(6):1107-1115．

(编辑:孙丰成)

Appraising well production changes in buried-hill fractured oil reservoirs by using the fractal theory

Wang Yuejie Tong Kaijun Cheng Dayong Zhang Hongyou Cheng Qi
(Bohai Oilfield Exploration and Development Institute，Tianjin Branch of CNOOC Ltd．，Tianjin，300452)

Taking JZ25-1 Soilfield in Bohai water as an example，the fractal theory was used to appraise the time-series changes of oil-well production in buried-hill fractured reservoirs，and the relationships of a fractal dimension with fluid type，oil well type and production program were established．It has been shown that the oil-well production contains significant fractal features，but a fractal dimension is largely independent of fluid type;that the fractal dimension of horizontal-well production is greater than that of directional-well production in the same well group，and that the fractal dimension of oil production is different under different production programs in the same well，and it will decrease gradually with increasing gradually the choke size and the pumping speed．The fracture development in reservoirs can be indirectly characterized by the fractal dimension of well production，and the greater the fractal dimension，the strongerr the fracture development in reservoirs，and the less the decrease of productivity index in oil wells．

buried-hill fractured reservoir;oil-well production;time series;fractal dimension;change; JZ25-1S oilfield

王月杰，女，工程师，主要从事油气田开发方面的研究工作。地址:天津市塘沽区609信箱(邮编:300452)。

2012-07-17