基于临界孔隙度模型的地震波传播

郭继亮，牛滨华，孙春岩，刘 畅

1 中国地质大学（北京），地球物理与信息技术学院，北京 100083

2 中国地质大学（北京），工程技术学院，北京 100083

1 引 言

本文使用弹性固体模型，弹性流体模型和临界孔隙度介质模型，通过运用等效用力学模型理论，建立流体饱和线性弹性孔隙模型.并结合波场模拟，研究该介质模型中地震波传播的特征和规律.对孔隙介质中地震波传播的研究由来已久.Biot理论被视为研究流体饱和孔隙介质弹性波传播的基础.Biot，M.A.承袭了 Von Terzaghi[1］的理念，将流体饱和孔隙介质作为一个整体来处理.Biot理论涵盖了高频波和低频波在流体饱和孔隙介质中的转播[2-3］.一些学者应用Biot理论对地震波在孔隙介质中的反射和透射进行了研究[4-5］.Zhu等[6］根据Biot理论，使用二维有限差分方法模拟了孔隙弹性储层的地震响应.Berryman和 Wang[7-8］发展了双孔介质理.Pride等[9］结合Biot理论，讨论了三种情况下P波在沉积岩中的衰减情况.Li等[10］基于Biot理论给出了二维在饱和圆弧形沉积河谷SV波散射问题的解析解.Chand等[11］比较了包括三相Biot模型的不同模型对含水合物沉积岩速度的描述.Dong等[12］结合Biot理论推导了三维半球形凹陷饱和土场地对平面P波散射问题的解析解.Wei等[13］以Biot理论为基础，讨论了黏滞流体饱和各向异性孔隙介质中弹性波的频散和衰减.Biot理论和以其为基础的研究取得了很大的成就，但这套理论的不利因素是参数较多[14］.

等效力学模型通过基本力学模型不同方式的组合，得到目标介质的应力应变关系，即本构关系.被广泛的应用于描述黏弹性介质中的应力应变关系，例如 Maxwell模型[15］和 Kelvin-Voigt模型[16-17］.临界孔隙度模型出现于20世纪90年代，Nur通过对大量岩石样品物性测量和分析提出了临界孔隙度和临界孔隙度模型[18-19］.此后 Mavko等[20］，Dvorkin等[21］，Mukerji等[22］和 Chen等[23］学者对临界孔隙度模型开展了进一步的研究.在此基础上牛滨华等[24-26］提出并实现了基于临界孔隙度模型各组分弹性参数的数值计算方法；并以此为基础进行了孔隙度介质对弹性模量的研究，提出了基于临界孔隙度模型的地震波传播研究的思路和方法[27-32］.本文承袭这个思路继续探讨孔隙度对介质弹性模量和地震波传播的影响.

本文研究工作的前提为：基本固体模型，流体模型，临界孔隙介质模型和目标介质模型为均匀弹性各向同性，流体与骨架完全耦合；基本力学模型和目标介质力学模型中的应力应变都是线性变化的.

2 基本理论

利用等效力学模型和临界孔隙度模型，建立流体饱和均匀弹性各向同性孔隙介质中的本构关系，进而建立该介质模型中的波动方程，研究孔隙和孔隙流体对介质弹性性质的影响.

2.1 基本力学模型和目标力学模型

在孔隙度从0到1的区间内，分布着三个基本力学模型和一个目标力学模型，如图1所示.两个固体型矢量弹性力学模型分别是孔隙度为0的S模型和孔隙度φE=φ的目标模型E；两个流体型标量弹性孔隙模型分别是孔隙度为φC的临界孔隙度模型C和孔隙度为1的流体模型F.其中S和F为骨架矿物和孔隙流体的成分，C代表临界孔隙度条件下的介质模型.

4个力学模型分布在两个孔隙度范围内：一，固体型矢量弹性区间，即孔隙度分布于 [0～φC）（模型S和C之间）的介质.这时介质整体呈固相，由矿物骨架承受压力起支撑作用.二，流体型标量弹性区间，即孔隙度分布于（φC～1］（模型C与F之间）的介质，这时介质整体呈流相，骨架颗粒在流体中呈悬浮态，流体承受压力起支撑作用.孔隙度为φC的C模型是固体型和流体型两类弹性孔隙流体介质的临界点，或称其为转换点.四种力学模型的弹性参数如表1所示.

图1 基本力学模型与目标模型之间关系示意图Fig.1 Relation between characteristic elements S、C，F and target element E

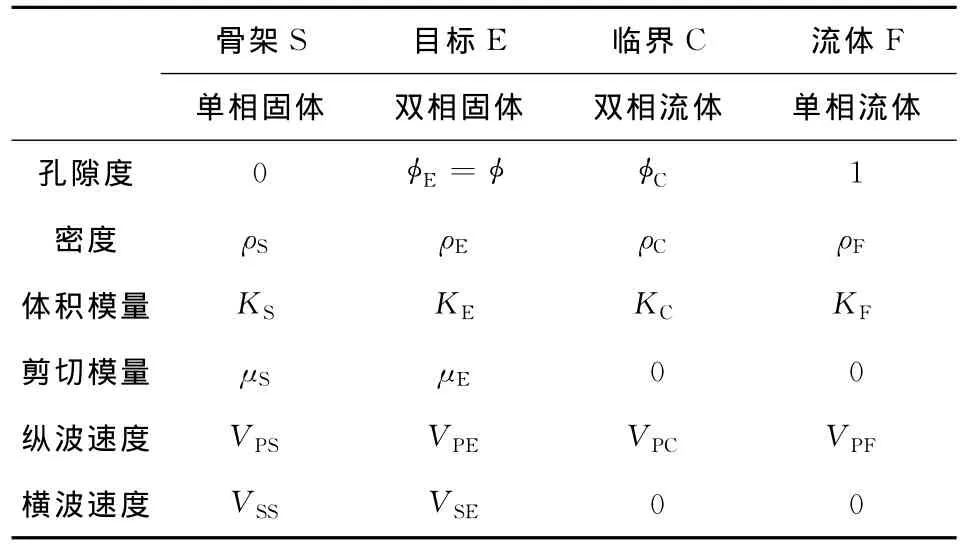
表1 四个力学模型的弹性属性参数表Table 1 Elastic parameters of the four elements

2.2 目标模型本构关系

运用等效力学模型，建立基本力学模型与目标力学模型的弹性参数之间的联系，即用基本力学模型的应力应变描述目标模型的应力应变关系.这时基本力学模型代表的骨架矿物、孔隙流体为流体饱和孔隙介质的组成部分，因此基本力学模型的弹性参数称为组分弹性参数.等效力学模型中的经典方法是：弹性模型与黏性模型的并联网络是等应变系统，该网络系统生成黏弹性固体型Voigt-Kelvin介质；弹性模型与黏性模型的串联网络是等应力系统，该网络系统生成黏弹性流体型Maxwell介质.文中利用在不同相态区间内的孔隙介质组分之间的等应力和等应变关系，通过等效力学模型，建立流体饱和孔隙介质中的本构关系.

流体饱和孔隙介质中，当介质处于矢量弹性区间内时，矿物骨架承压，矿物骨架模型和孔隙流体模型的应变相同，类似Voigt-Kelvin介质中的固体弹性模型和黏性流体模型.当介质模型是流体处在标量弹性区间内时，骨架矿物悬浮于流体中，流体承压，矿物骨架模型与流体模型所受应力相同，类似Maxwell介质中的固体弹性模型和黏性流体模型.可以视骨架矿物和孔隙流体为对应的单相固体矢量弹性介质和单相流体标量弹性介质，结合临界孔隙度模型，运用等效力学模型方法构建目标孔隙流体介质模型.

3 目标孔隙介质模型构建

目标介质模型E的体积模量和剪切模量的构建都包含了一次模型等应力组合和一次模型等应变组合.如图1所示，通过两步建立模型E的弹性模量组分表达式.第一步：依据等应力条件，将S和F弹性模量加权组合得到C的弹性模量；第二步：依据等应变条件，将C与S的弹性模量加权组合得到E的弹性模量.

3.1 力学模型的应力与应变关系

下面介绍四种介质中的应力应变关系.模型S和E为固体型矢量弹性介质，其体积模量由下述式子表示：

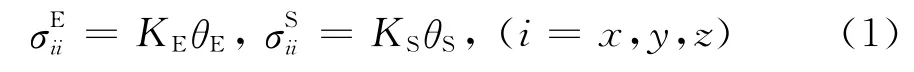
式中，模型E的压力PE与三个正应力的关系是体积应变系数θE与三个正应变的关系是同理，对于模型S有，模型S和E的剪切模量由下述式子表示：

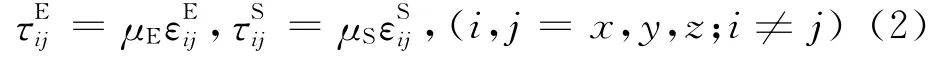
模型C和F为流体型标量弹性介质，其体积模量可以写成：

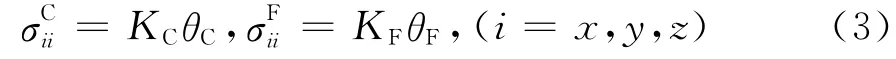
模型C和F的剪切模量均为0，即，

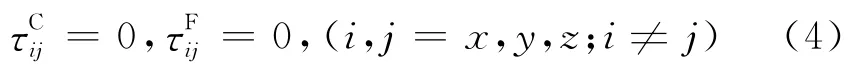
上述（1）至（4）式的应力与应变关系都可以视为本构关系的一种表达形式.

3.2 体积模量的组分表达形式

在均匀各向同性条件下，体积模量、剪切模量和密度可以完整表现介质的弹性属性.体积模量和剪切模量的定义表达式是本构关系的一种表达形式，因此可以用这样的表达式刻画相关模型的弹性.

首先求取临界体体积模量的组分表达形式.弹性流体模型C可以由弹性固体模型S和弹性流体模型F的等应力组合表示.这种等应力组合表明，C的体积应变等于S和F两者体积应变的加权组合.等应力组合的应变加权系数分别为（1-φC）和φC，于是有

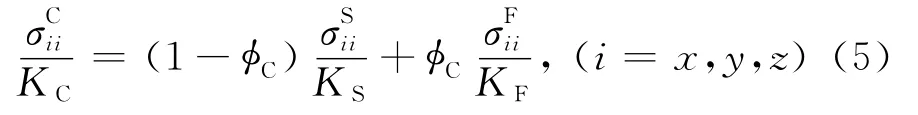
两个力学模型的串联系统是等应力系统，即PC=则有

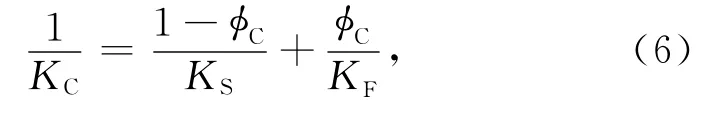
上式是KC关于KS和KF的组分方程.方程（6）的形式与Nur给出的临界点KC的体积模量表达形式一致，这也从等效力学模型角度，对临界理论提供了一种解释.

下面推导目标模型体积模量的组分表达形式.弹性固体型E可以由弹性固体模型S和弹性流体模型C的等应变组合表示.这种等应变组合表明，E的正应力等于S和C两者正应力的加权组合.应力加权系数分别为于是有，

式中孔隙度φ满足0≤φ＜φC.S和C两个力学模型等应变组合，即θE=θS=θC；则有

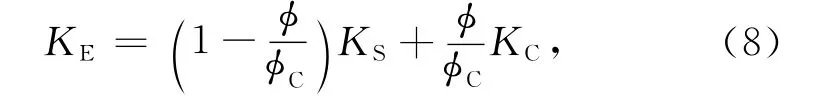
式（8）称为KE的组分表达形式，即KE的组分方程.

3.3 其它参数的组分表达形式

运用类似的方法得到E的剪切模量的组分表述式.E的切应力等于S和C两者切应力的加权组合.应力组合的加权系数分别为于是有，

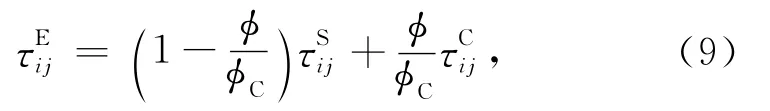
式中孔隙度φ满足0≤φ＜φC.把（2）式和（4）式代入（9）式，得到μE的组分表达形式

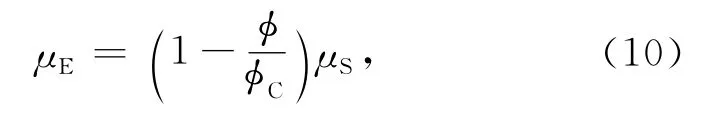
目标介质模型E的密度ρE表达式就是众所周知的密度组分方程即，

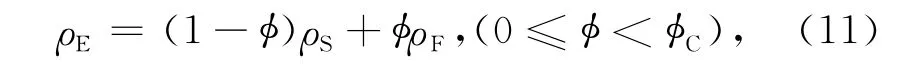
由目标介质模型弹性参数的组分表达形式可得到这种介质中纵波和横波的相速度组分表达形式.纵波和横波的相速度组分表达式为

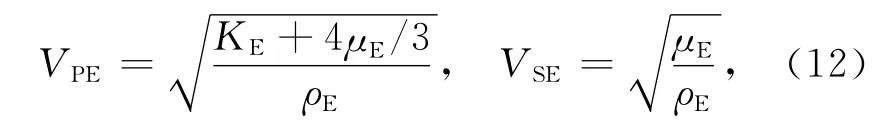
上述过程得到的体积模量和煎切模量的组分表达式与Nur等提出的临界孔隙介质模型中的弹性参数表达式完全一致；这也验证了Nur等临界孔隙度模型的正确性.

3.4 本构方程和弹性矩阵

得到介质模型E弹性参数的组分表达形式后，讨论该介质模型的本构关系.由于介质为均匀弹性各向同性，本构方程的组分形式可以通过求取该介质弹性矩阵中弹性参数的组分表达形式的方法得到，也可直接由推导该模型中介质应力应变关系得到.

3.4.1 弹性矩阵组分表达形式

基于前面得到的模型E的体积模量KE、剪切模量μE的表达式，根据均匀弹性各向同性介质弹性矩阵的结构特点，可以得到E的弹性矩阵CE6×6的表达式：

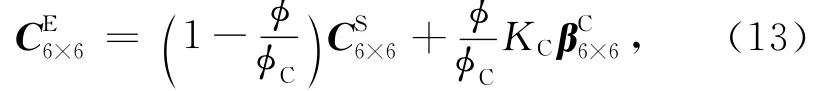
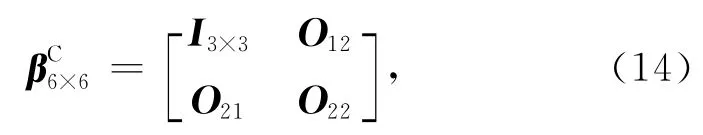
模型E的本构方程可以写成：

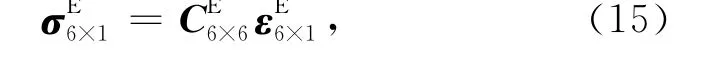
3.4.2 应力应变关系的组分表达形式

针对给的4个力学模型的本构关系，运用等效力学原理，讨论目标介质E的本构关系和弹性矩阵.介质模型E是通过模型S和C通过等应变组合构建而成，E所受的应力为S和C的应力线形组合，所以存在以下关系

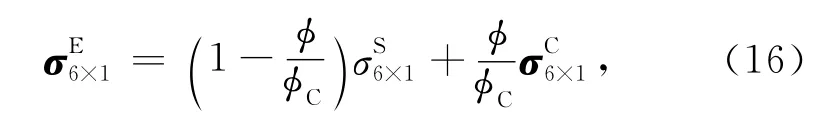
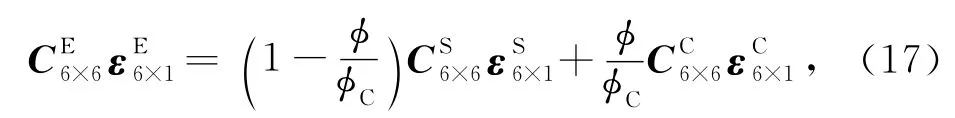
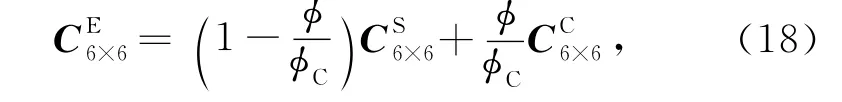
由上面的本构关系可以得到均匀弹性流体饱和孔隙介质中的波动方程，其具体形式为

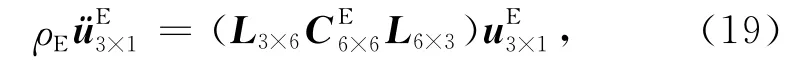
4 数值模拟

为检验孔隙对地震波传播的影响，基于矢量弹性流体饱和孔隙介质的波动方程，运用旋转交错网格有限差分方法对二维孔隙介质模型（XOZ面）进行弹性波场数值模拟.波场模拟中模型组分的弹性参数见表2.饱水模型的弹性参数参考了Berger在Lawrence Livermore National Laboratory进行的流体饱和人工合成砂岩孔隙度-波速关系的物理模型试验[33］.

表2 饱水介质在组分的弹性参数Table 2 Elastic parameters of components of porous media

根据表2中的骨架和流体的弹性信息以及临界孔隙度值，通过临界孔隙度模型计算，可以得到不同孔隙度条件下目标模型的弹性参数，如图2所示，根据方程（8），（10），（11）和（12），随着孔隙度的增长，介质的整体弹性参数随之下降，相应的整体速度也随之减小.当孔隙度小于在临界值时，随着孔隙度增大整体体积模量（除临界点）、整体剪切模量和整体密度的变化正比于孔隙度变化；而速度的变化在靠近临界孔隙度的区域更加明显，即减小得更快.这符合临界孔隙度模型对介质的描述.整体纵波波速从孔隙度为0时的6000m／s降到孔隙度为临界值时的1597.4m／s，减少了73.4%；相应的整体横波速度由3464.2m／s降到0m／s，减少了100%；相应的整体密度值由2500kg／m3降到1772.9kg／m3，减少了29.1%.

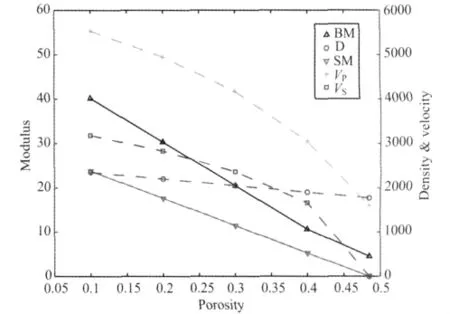
图2 目标模型孔隙度与弹性参数关系图实线图对应模量坐标，其中BM代表体积摸量，SM代表剪切模量，虚线图对应速度密度坐标，其中D代表密度，VP代表纵波速度VS代表横波速度.Fig.2 Relation between porosity and elastic parameters of E Solid lines show modulus；BMmeans bulk modulus and SM means shear modulus，dash lines show velocities and densities；D，VPand VSrespectively mean density Pwave velocities and S wave velocities.

如图3a所示，模型被离散为网格距为2m的方形网格，共512×1024个网格点.模型分为两层，层位置为z=512m，在模型的上半部分，也就是I区域中，介质的孔隙度为0，在模型的下半部分，即区域II中，介质的孔隙度分别为0.1，0.2，0.3，0.4和0.4847，孔隙中饱水.位于坐标（1024，10）的震源为主频60Hz的Ricker应力子波，采用不同垂向应力和切向应力组合的纵横波偶合震源.模拟的时间步长为0.2ms.两个观测点的坐标为（600，0）和（600，600）.采用时间二阶精度，空间四阶精度的算法.

分别对以上5个不同孔隙度的模型进行数值模拟，t=190ms时X分量的波场快照如图3（b-f）所示.

由图3可以看出，波在介质I和介质II的分界面发生反射和透射.随着孔隙度的增加，介质II中的整体纵横波速度变小.另外，孔隙度为0，0.1，0.2，0.3，0.4对应的波场3（b-e）中II区域中同时存在纵波和横波，因为这时的介质都是矢量弹性的；而孔隙度为临界值φC=0.4847的图3f的波场中仅有纵波成分，因为这时的介质是标量弹性的.孔隙度增大过程中反射波的能量逐渐增加，透射波的能量逐渐减小.

两个观测点的地震记录如图4所示，地表接收点（坐标（600，0））位于区域I中，接收反射记录；地下接收点（坐标（600，600））位于区域II中，接收透射记录.反射记录中三个波形从左至右依次为PP波反射，PS+SP波反射和SS波反射记录，由于反射波在介质区域I中传播，不同模型中反射波的走时相同，但由于孔隙度导致的分界面波阻抗差异，反射波振幅随区域II中介质孔隙度增大而增大如图4a所示.透射记录中除临界孔隙介质外各个记录中均存在PP，PS，SP和SS四种波的波形，临界孔隙介质中只含PP和SP两种波形，弹性波走时随区域II中介质孔隙度增大而增大，如图4b所示.

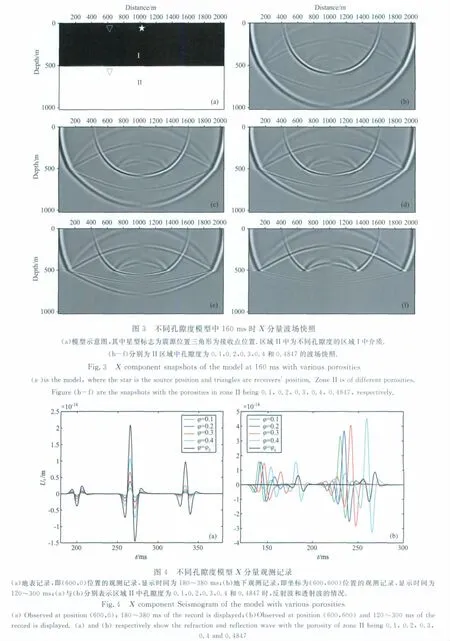
通过对孔隙和孔隙流体导致的空间弹性参数差异的模型进行数值模拟，直观的反映了孔隙和孔隙流体对弹性波传播的影响.也验证了临界孔隙度模型地震建模的效果.

5 结 论

本文利用等效力学模型原理，将弹性固体模型、弹性流体模型和临界孔隙度模型进行线性组合，得到了弹性（即无黏性）饱和流体孔隙介质模型，主要结果如下：

（1）运用等效力学模型构建流体饱和组分弹性孔隙介质的本构关系.本文基于孔隙介质组分的弹性关系，利用临界孔隙度模型，通过应用等效力学模型，建立了流体饱和组分弹性孔隙的本构关系.本构关系中弹性矩阵的具体形式可以通过求取该介质弹性矩阵中弹性参数的组分表达形式的方法得到，也可直接由推导该模型中介质应力应变关系得到.

（2）在构建模型的过程中引入了临界孔隙度模型，并将临界孔隙介质模型作为一个基本力学模型单元.临界孔隙模型的引进不仅给出了孔隙介质的相态变化点，也将矿物骨架模型和孔隙流体模型有机的联系在一起，将临界孔隙介质模型作为目标模型的直接组成部分.利用等效力学模型得到的临界孔隙介质的弹性参数表达其形式与Nur给出的经验公式形式一致，这也从等效力学模型角度，证明了线性应力应变前提下，临界孔隙模型的正确性.

（3）通过数值模拟，在组分模型的前提下，初步探讨了孔隙和孔隙流体对地震波传播的影响.通过数值模拟初步表现了介质中孔隙对反射波和透射波传播速度和振幅速度的影响.

6 讨 论

实际介质中孔隙和孔隙流体对地震波传播有多方面影响.本文通过临界孔隙度模型讨论完全弹性条件下孔隙和孔隙流体对地震波传播的影响.未考虑孔隙流体的黏性，流体与骨架耦合关系和孔隙的散射作用等因素对地震波的影响，这也是我们下一步研究的重点.本文中的均匀弹性各项同性前提下的工作不但是研究流体黏性对地震波研究的前提，也是研究各向异性孔隙介质地震波研究的基础.从本构关系角度讲，组分模型地震波传播的工作可以很好的和经典黏弹性介质和各向异性介质地震波传播的工作相结合.

（References）

[1]Terzaghi K.Auftrieb und Kapillardruck an betonierten Talsperren.Die Wasserwirtschaft，1933，（26）：397-399.

[2]Biot M A.Theory of propagation of elastic waves in a fluidsaturated porous solid：I.Low-frequency range.Acoust.Soc.Am.，1956，28（2）：168-178.

[3]Biot M A.Theory of propagation of elastic waves in a fluidsaturated porous solid：II.higher frequency range.Acoust.Soc.Am.，1956，28（2）：179-191.

[4]Hajra S，Mukhopadhyay A.Reflection and refraction of seismic waves incident obliquely at the boundary of a Liquidsaturated porous solid.Bulletin of the Seismological Society of America，1982，72（5）：1509-1533.

[5]Deresiewicz H.The effect of boundaries on wave propagation in a Liquid-filled porous solid：IV.surface waves in a halfspace.Bull.Seism.Soc.Am，1962，52（3）：627-638.

[6]Zhu X，McMechan G A.Numerical simulation of seismic responses of poroelastic reservoirs using biot theory.Geophysics，1991，56（3）：328-339.

[7]Berryman J G，Wang H F.The elastic coefficients of doubleporosity models for fluid transport in jointed rock.Journal of Geophysical Research-Solid Earth，1995，100（B12）：24611-24627.

[8]Berryman J G，Wang H F.Elastic wave propagation and attenuation in a double-porosity dual-permeability medium.International Journal of Rock Mechanics and Mining Sciences，2000，37（1-2）：63-78.

[9]Pride S R，Berryman J G，Harris J M.Seismic attenuation due to wave-induced flow.Journal of Geophysical Research-Solid Earth，2004，109：B01201，doi：10.1029／2003JB002639.

[10]李伟华，赵成刚.饱和土沉积谷场地对平面SV波的散射问题的解析解.地球物理学报，2004，47（5）：911-919.Li W H，Zhao C G.Scattering of plane SV waves by circular arc alluvial valleys with saturated soil deposits.Chinese J.Geophys.，2004，47（5）：911-919.

[11]Chand S，Minshull T A，Gei D，et al.Elastic velocity models for gas-hydrate-bearing sediments—a comparison.Geophysical Journal International，2004，159（2）：573-590.

[12]董俊，赵成刚.三维半球形凹陷饱和土场地对平面P波散射.地球物理学报，2005，48（3）：680-688.Dong J，Zhao C G.An analytic solution for the diffraction of plane P-wave by three-dimensional hemispherical canyons in a fluid-saturated porous media half space.Chinese J.Geophys.（in Chinese），2005，48（3）：680-688.

[13]魏修成，卢明辉，巴晶等.含黏滞流体各向异性孔隙介质中弹性波的频散和衰减.地球物理学报，2008，51（1）：213-220.Wei X C，Lu M H，Ba J，et al.Dispersion and attenuation of elastic waves in a viscous fluid-saturated anisotropic porous solid.Chinese J.Geophys.（in Chinese），2008，51（1）：213-220.

[14]陈颙，黄庭芳，刘恩儒.岩石物理学.安徽：中国科学技术大学出版社，2009.Chen Y，Huang T F，Liu E R.Rock Physics（in Chinese）.Anhui：Press of University of Science and Technology of China，2009.

[15]Maxwell J C.On the dynamical theory of gases.Phil.Trans.Roy.Soc.London，1867，157：49-88.

[16]Kelvin L.Vortex statics.Collected works，1875，IV：115-128.

[17]Voigt W.Uber innere reibung fester korper，insbesondere der metalle.Annalen der Physik，1892，283（12）：671-693.

[18]Nur A.Critical porosity and the seismic velocities in rocks.EOS.Trans.Am.Geophys Union，1992，73：43-66.

[19]Nur A，Marion D，Yin H.Wave velocites in sediments.／／Hovem J M，Richardson M D，Stoll R D，eds.Shear Wave in Marine Sediments.Dordrecht：Kluwer Academic Publisher，1991：131-140.

[20]Mavko G， Mukerji T，Dvorkin J.The Rock Physics Handbook.New York：Cambridge University Press，1998.

[21]Dvorkin J，Prasad M，Sakai A，et al.Elasticity of marine sediments：Rock physics modeling.Geophysical Research Letters，1999，26（12）：1781-1784.

[22]Mukerji T，Berryman J， Mavko G，et al.Differential effective medium modeling of rock elastic moduli with critical porosity constraints.Geophysical Research Letters，1995，22（5）：555-558.

[23]Chen Q，Nur A.Critical concentration models for porous materials.／／ Corapcioglu M Y，ed.Advance in Porous Media.New York：Elsevier.1994：169-308.

[24]牛滨华，孙春岩，闫国英等.含气介质临界点，流体和骨架弹性参数的数值计算方法.地球物理学报，2010，53（6）：1495-1501.Niu B H，Sun C Y，Yan G Y，et al.Numerical calculation method for getting critical point，pore fluid and framework parameters of gas-bearing media.Chinese J.Geophys.（in Chinese），2010，53（6）：1495-1501.

[25]牛滨华，郭继亮，孙春岩.CLYJ饱水石灰岩骨架和流体弹性参数估算.地球物理学报.2011，54（10）：2652-2664.Niu B H，Guo J L，Sun C Y，et al.Estimating elastic parameters of framework and pore fluid from CLYJ saturated limestone samples.Chinese J.Geophys.，2011，54（10）：2652-2664.

[26]Niu B，Sun C Y，Yan G Y，et al.Linear numerical calculation method for obtaining critical point，pore fluid，and framework parameters of gas-bearing media.Applied Geophysics，2009，6（4）：319-326.

[27]贾冀辉，牛滨华，孙春岩等.水合物密度的数值计算及储层识别.现代地质，2011，25（6）：1180-1186.Jia J H，Niu B H，Sun C Y，et al.Density calculation and reservoir identification of gas hydrates.Geoscience（in Chinese），2011，25（6）：1180-1186.

[28]牛滨华，孙春岩，李明.半空间介质与地震波传播.北京：石油工业出版社，2002.Niu B H，Sun C Y，Li M.Seismic Wave Propagation in Half Space Media （in Chinese）.Beijing：Petroleum Industry Press，2002.

[29]牛滨华，孙春岩.固体弹性介质与地震波传播：半空间均匀各向同性单相.北京：地质出版社，2005.Niu B H，Sun C Y.Seismic Wave Propagation in Single Phase Homogeneous Isotropic Half Space Media（in Chinese）.Beijing：Geological Puldishing House，2005.

[30]牛滨华，孙晟，孙春岩等.Biot介质密度参数的容差密度表达.现代地质，2007，21（3）：551-556.Niu B H，Sun S，Sun C Y，et al.Expressions of density Parameters of Biot medium with differential density.Geoscience（in Chinese），2007，21（3）：551-556.

[31]邹荃，牛滨华，孙春岩等.饱水石灰岩骨架和流体弹性参数的估算.石油地球物理勘探，2011，46（5）：763-768.Zou Q，Niu B H，Sun C Y，et al.Estimation of component elastic parameters from saturated limestone samples.Oil Geophysical Prospecting （in Chinese），2011，46（5）：763-768.

[32]张艳，牛滨华，孙春岩等.基于典型饱水砂岩样品的多维空间多元统计密度反演方法.现代地质，2011，25（6）：1174-1179.Zhang Y，Niu B H，Sun C Y，et al.Density inversion of typical water-saturated sandstones with multivariate statistical analysis in multidimensional space.Geoscience（in Chinese），2011，25（6）：1174-1179.

[33]Berge P A，Bonner B P，Berryman J G.Ultrasonic velocityporosity relationships for sandstone analogs made from fused glass beads.Geophysics，1995，60（1）：108-119.