2011年日本东北大地震特低频地磁信号的分形标度特征研究

荣扬名，王 桥，丁 霞，黄清华

北京大学地球与空间科学学院地球物理学系，北京 100871

1 引 言

大量与地震相关的电磁观测资料和研究成果在一定程度上证实了地震电磁现象的客观存在性，地震电磁观测作为一种前兆监测方法已在地震预测研究中发挥了一定的积极作用[1-12］.地震电磁现象中的特低频（Ultra-Low-Frequency，ULF，根据国际电联和国内通信界称谓的特低频为小于3Hz的频带范围）电磁现象更是被认为是一种有潜力的前兆现象而受到了广泛的关注[4-12］，也带动了关于特低频电磁现象物理机制的理论模型、实验和数值模拟等研究[1-2，13-15］，只是由于实际地下结构和孕震过程的复杂性，当前对包括特低频在内的地震电磁现象的认识还比较有限，尚有待进一步的研究.

另一方面，研究表明地震和其它一些自然灾害系统呈现出典型的非线性自组织临界状态（selforganized criticality，SOC）[16-17］.自组织临界性的基本图像是，大自然在某处永久的偏离平衡，却又被组织在一种稳定状态中——一种临界状态：各种事件都能按照完全确定的统计规律——幂律发生.自组织临界性理论是一种新型的统计理论，不依赖于系统的初始条件和任何细节部分.系统演化行为遵从幂律分布，而服从幂律分布的动力学系统表明系统内部存在自相似性.因此，自组织临界性被猜测是相互作用的多体系统所具有的典型行为，它无论是在时间上还是空间上都具有丰富的分形结构.国内外已经在地磁和地电时间序列的分形分析方法和实际数据分析上做了大量的工作[9，18-19］，相关的数学处理手段和科学分析得到了很大程度的发展.本文采用的去倾扰动分析方法（Detrended Fluctuation Analysis，DFA）即是一种有效的数学分析方法，最先在20世纪90年代由Peng用于医学研究，用来分析心跳间隔时间序列、DNA序列和其他生理信号记录的分形标度特征[20-21］.近几年，意大利的Telesca等研究了DFA方法在处理地学信号记录方面的有效性，研究对象包括与地震和火山活动相关的地电、地磁和自电位信号记录，得到了信号分形标度异常与相应地震火山活动比较好的关联性[22-24］.然而，以往的研究结果大多限于单台数据，且缺乏统计显著性方面的检验，这在一定程度上制约了相关结论的可信度.

2011年3月11日在北纬38.103°，东经142.861°发生的日本东北部Mw9.0级大地震是有现代地震记录以来最大的地震之一，并伴随着一系列的余震活动.位于该地区附近的电磁台站采集到了震前一段时期和余震持续期间的ULF地磁信号，这无疑为进一步探讨ULF地磁信号异常与地震活动之间的关联提供了一次良好的机会.

本文尝试运用DFA方法处理2010年1月1日到2011年4月30日之间485天ULF地磁记录的秒值（1Hz）和分钟值（1／60Hz）地磁记录，数据来源于大地震发生区域附近的 Kakioka（KAK，36.232°N，140.186°E）、Haramachi（HAR，37.615°N，140.953°E）和 Yokohama（YOK，40.993°N，141.240°E）三个地磁台站.我们基于以上方法研究了24h单位长度的地磁时间序列分形标度特征，结合前人的研究，定量分析了非均匀标度特征的时间变化，提出了一种能反映地磁三分量非均匀标度特征同步变化的新指标，并据此探讨了特低频地磁信号分形标度特征变化与日本东北大地震之间的可能关联性，并对得到的信号异常进行统计显著性方面的检验，以提高异常的可信度.

2 观测资料和分析方法

本文研究了来自日本东北大地震区域附近三个地磁观测台站的ULF地磁信号记录，分别是作为国际地磁基准台的KAK的1Hz数据，以及来源于另外两个地磁连续观测台站HAR和YOK的分钟值数据（1／60Hz），数据记录时间为2010年1月1日至2011年4月30日共485天.三个台站的分布见图1，所选取的研究区域和时间的地震事件也在图1标出.

我们采用的DFA方法是处理时间序列分形特征的一种统计学方法，它能去除人为造成的标度关联性的一些信息.

第一步：对于时间序列x（i），i=1，2，…，N，求得序列的平均值，用下式求得一个新的序列：

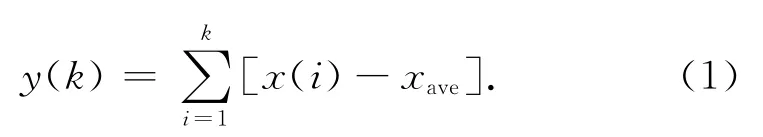
第二步：将总长为N的积分时间序列分成等长，取每份为n的窗，n的取值范围从4到N／4.

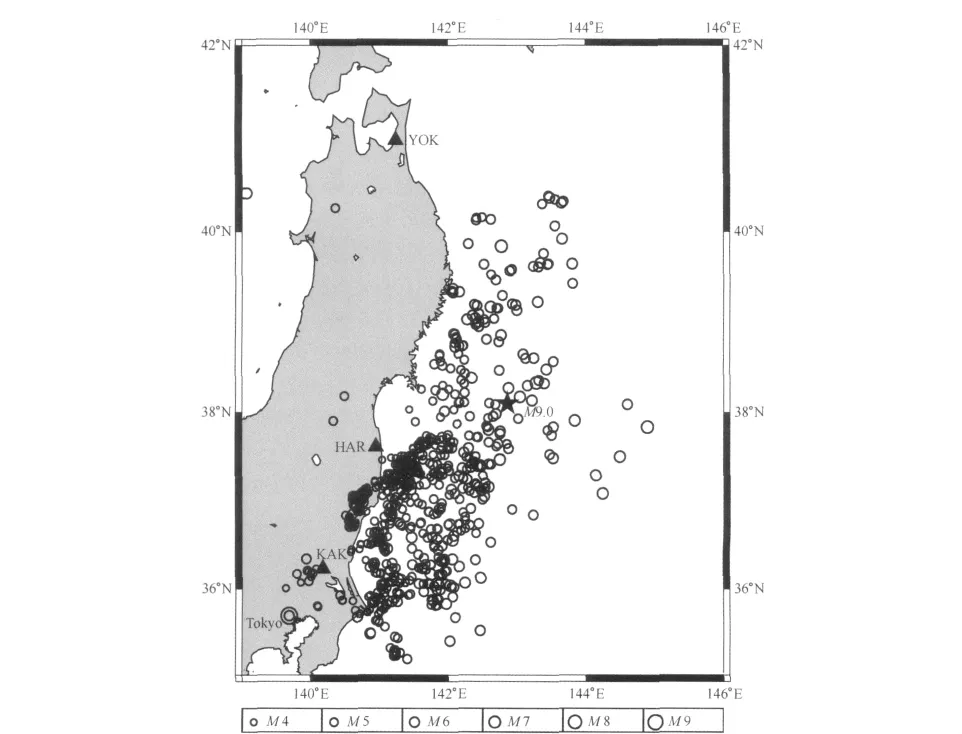
图1 台站及震中分布图.圆圈标示的是研究区域中2010／01／01—2011／04／30期间大于4级的地震，五角星表示2011／03／11 M9.0.东北大地震的震中（38.103°N，142.861°E），三角形为三个台站 KAK、HAR和 YOK的位置Fig.1 Distribution of the geomagnetic stations and the epicenter of earthquakes in the investigated region.The circles indicate the earthquakes with magnitude≥4.0which occurred from 2010／01／01to 2011／04／30；the triangles show three stations；the star shows the epicenter of Tohoku earthquake（38.103°N，142.861°E）

第三步：对每个长为n的数据序列进行最小二乘法线性拟合，代表此数据窗的倾向.线性拟合后得到的y轴坐标记作yn（k）.进行去倾处理，即在每个窗里用y（k）减去相应的局部倾向yn（k），然后得到用下式计算的均方根

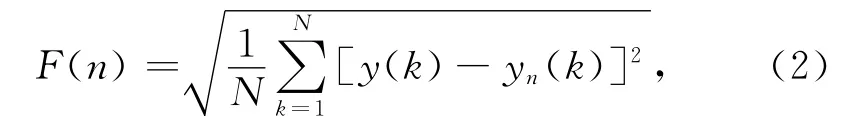
这里N是序列的总长度.

第四步：对每个窗口标度重复第三步的运算，我们可以得到F（n）-n的一一对应关系，代表了每个窗口标度n的平均的扰动情况；

第五步：如果F（n）对n的关系符合幂律，即

将F（n）-n画在双对数坐标系中应呈一直线，此直线的拟合斜率便是目标时间序列对应的标度特征指数α.

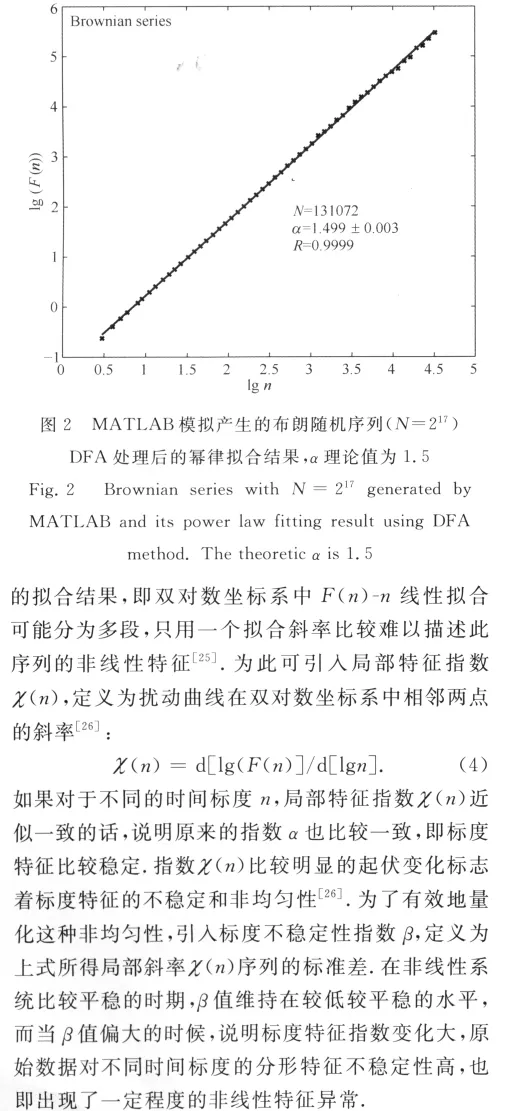
对于白噪声随机序列，α值理论上为0.5，但如果序列过短，初始拟合斜率可能跟0.5有所偏差，当序列长度足够大时，会无限逼近0.5；当α＞0.5时表明此序列具有强的长程相关性，即相对均值较大的值后边出现较大的值几率比较大，反之亦然；当α＜0.5时表明一种弱的长程相关性，即对均值较大的值后边出现较小的值几率比较大，反之亦然；α=1表明此序列是典型的闪烁噪声或者说1／f信号过程；α=1.5表明是典型的布朗随机过程[21］.作为一个例子，图2给出了MATLAB产生的布朗随机过程序列数值模拟的结果，序列长为217，拟合结果与理论值α=1.5吻合的很好.

但对于实际数据的时间序列，往往得不到单一

(1)确定整体教学目标：学生完成该课程的学习应达到的具体知识、能力、素质目标，并分别指出中职、高职阶段应分别达到的目标，教学目标应该量化并具有可执行性。

由本文的具体数据，即每日的地磁东西分量（EW）、南北分量（NS）和垂向分量（Z）的三分量序列，可以得到三个β序列，这三个序列各包含地磁分量的分形信息，如果有大的扰动应该也包含一定的异常.为了既凸现三分量同步的异常信息，又能抑制各分量中可能出现的零星干扰，我们提出了一种新的标度不稳定性指标βXYZ，具体将每日三分量的标度不稳定性指数β取乘积，以此来表征总的标度变化效应，即βXYZ=βEW＊βNS＊βZ.

3 结 果

我们用DFA方法处理了KAK台站485天1Hz的地磁数据，数据包括地磁场东西分量（EW）、南北分量（NS）和垂向分量（Z）的三分量时间序列.图3给出了运用DFA方法获得的双对数坐标系中标度与扰动状况幂律拟合的例子.从图3a中可以看到对不同标度的拟合斜率比较一致，说明对所取的时间标度存在相近的扰动状况，即分形特征比较一致，这种只用单一斜率就能描述整体拟合的情形对大多数天数都适用；而从3b和3c两幅图中看出，部分拟合曲线分为明显的两段或三段，中间存在转折点（crossover），反应了不同标度扰动情况的非均匀性，而且这些转折点对应的标度以及各段的拟合斜率也不尽一致；更有极少情况，如3d图所示，虽然可以看出大致的线性拟合趋势，但是拟合点分布过于分散，拟合相关系数相对较小.

结合以上分析，从每日的DFA幂律拟合结果并不是都能得到唯一对应的标度指数α，不同的标度范围拟合得到的α可能不同.正因为存在这种不一致性，我们如方法中所述选择分析扰动变化曲线的标度不稳定指数β，这样能更有效地反映非线性系统的非均匀标度特征变化.

为了更好地分析β值的变化，可取β的滑动平均值（本文取11天滑动平均）作为参考指标.图4（a-c）分别给出了KAK、HAR和YOK三个台站EW地磁分量标度不稳定指数β滑动平均值的变化，为便于比较，取其均值加2倍均方根作为异常的判定阈值（图中用虚线表示）.结果表明三个台站的地磁EW分量对应的滑动平均β值都在2011年3月11日大规模地震事件前25～50天左右出现了异常增大现象，其中，KAK异常出现时间为2011／2／15—2011／2／18，HAR 和 YOK 为 2011／1／20—2011／1／30.其他分量所对应的β值在震前这段时期内也基本维持在相对较高的水平.

需要指出的是，上述三个台站中HAR台EW分量的β值在其他时间也出现了两次相对较弱异常（图4b），分别为2010／4／10—2010／4／11的异常1以及2010／10／12的异常2，且这两次异常的持续时间较短（均不超过两天），此外，同时期的全球地磁活动Ap值（图4d）显示2010／4／5-6两天的Ap值分别高达55和44，异常1可能与此地磁活动有一定的关联，因为图4b反映的是11天滑动平均的结果，至于异常2，考虑到其只在一个台站的一个分量图中出现，持续时间也较短，可能是由于台站附近局部范围的扰动所致.

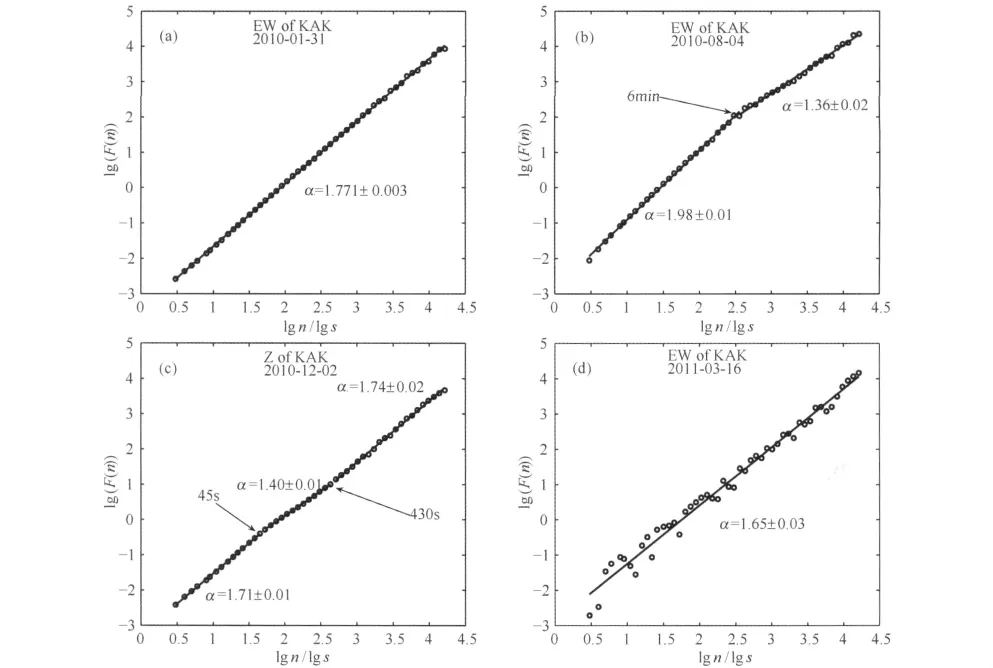
图3 DFA方法处理KAK三分量地磁数据得到的幂律拟合示例（a）用一个标度特征指数就可以描述数据的标度特征.（b）-（c）需要两或三个分段特征指数才能描述标度特征.（d）图虽也能看出较好的拟合趋势，但数据点的分布过于离散.Fig.3 Examples of power law fitting curves for the investigated data of KAK（a）Single scaling exponent；（b）Two scaling exponents；（c）Three scaling exponents；（d）Single power law fitting of scattered data.

考虑到单一地磁分量的异常可能并不足以反映非线性系统整体的异常情况，本文提出了综合考虑三分量的标度不稳定指数β并取其乘积的一种新指标，即βXYZ=βEW＊βNS＊βZ，该指标能有效地反映地磁三分量内在的非均匀标度特征的同步变化.图5给出了三个台站11天滑动平均结果.从图中可以看出，单一分量中出现的个别异常基本得到了较好的抑制，而图4中显示的三个台在日本东北大地震前25～50天左右出现的异常在图5中也有明显体现.KAK台站滑动平均值（图5a）在2011／3／11—2011／3／21期间出现了非常显著的异常变化，这可能与日本东北大地震及其余震等地震活动有关.事实上，YOK台也出现了类似的可能与该地震余震活动相关的异常变化，只是幅度不如KAK显著.考虑到KAK台在主震及余震期间出现的异常过于显著，可能会在一定程度上掩盖震前的可能的变化，为此，我们重新分析了KAK台截至日本东北大地震前的变化，即不分析地震及余震持续期间的βXYZ而关注震前的βXYZ并作相应的滑动平均处理（图5d），结果表明在2011／2／13—2011／2／23出现了超出阈值的情况，即震前25天左右开始βXYZ值相对背景值明显增大，同时期Ap值（图4d）相对较小，表明该异常并非全球地磁扰动所致.HAR台滑动平均值在2011／1／24—2011／1／30出现了明显超出阈值的异常现象（图5b），该异常大约始于东北大地震46天前.YOK 台站滑动平均值在2011／1／20—2011／1／30期间出现了较明显的异常（图5c），该异常在东北大地震前50天左右出现，与HAR台同期的异常吻合较好.总之，无论是从地磁单分量的变化特征（图4），还是从同时考虑三分量信息的综合指标（图5）来看，三个台在日本东北大地震前25～50天左右都出现了非均匀标度特征的显著异常变化，这种基本一致的异常现象可能反映了该地震对地磁时间序列内在的非线性系统的影响.

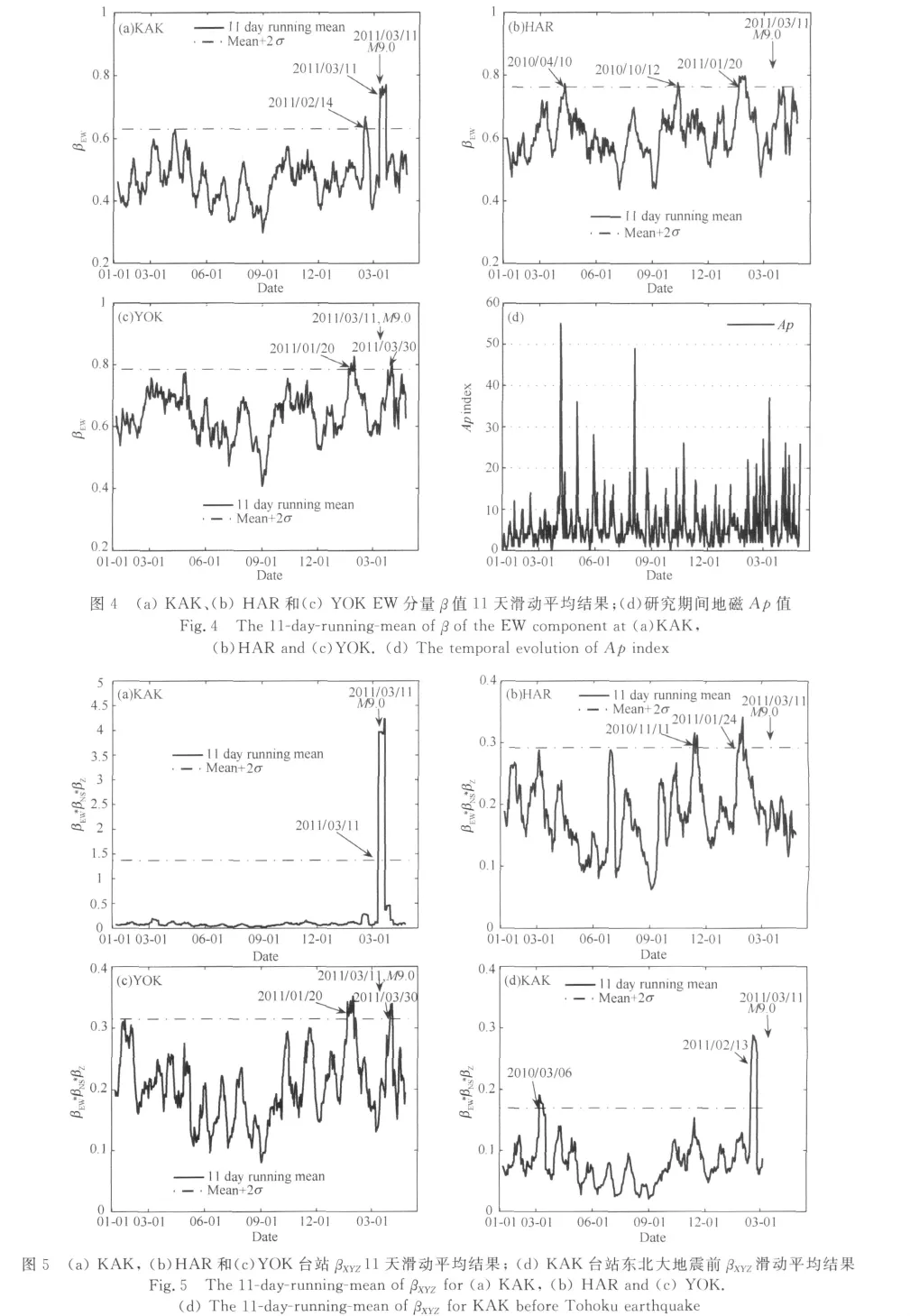
除了在日本东北大地震前25～50天左右以及余震期间出现的异常之外，HAR台在2010／11／11（图5b），KAK台在2010／3／6（图5d）也分别出现了非均匀标度特征的异常，但这两次异常仅在单台出现，而且相应的地磁单分量在对应的时间段并未出现显著异常（图4），因此，这两次异常的可信度并不太高.

4 讨 论

研究表明，地震等构造活动可能导致ULF地磁信号的 分 形 特 征 异 常 变 化[9，19，25］.在 地 震 活 动 水平相对较低的阶段，构造系统的自组织临界性质能令ULF地磁信号的分形标度特征变化维持在比较稳定均匀的程度，而在强震等来临前该非线性系统会逐渐失稳，进而导致ULF信号出现了较大的分形标度异常变化.运用统计分形分析方法可从实际观测到的地磁信号中提取出这种分形异常特征，有助于加深对地震及其孕育过程的理解.

鉴于以往的研究大多限于单台数据，且缺乏统计显著性方面的检验，相关结论的可信度有待进一步的研究，本文提出了一种能反映地磁三分量非均匀标度特征同步变化的新指标，并据此探讨了ULF地磁信号分形标度特征变化与日本东北大地震之间的可能关联性.结果表明，震区附近三个台的ULF地磁信号在日本东北大地震前25～50天左右都出现了非均匀标度特征的显著异常变化，其中，HAR和YOK两个台站的异常起始时间比较一致（图4，图5），而KAK略晚，这可能与地震孕育过程本身的复杂性有关，也可能受到实际条件下地震电磁信号选择性特征的影响[27-29］.

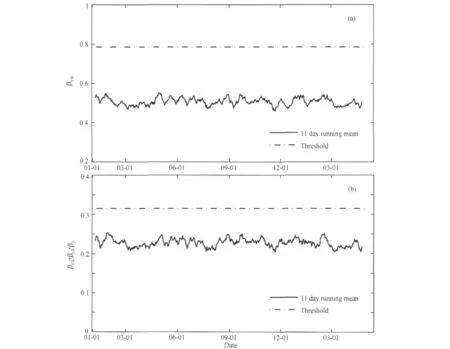
图6 磁静日随机合成数据统计检验结果（a）合成EW分量β值11天滑动平均结果，虚线表示与实际数据得到的阈值（0.785）比较；（b）合成三分量数据的βXYZ11天滑动平均结果与实际阈值（0.315）比较.Fig.6 Stochastic test using the synthetic geomagnetic data with randomized disturbances（a）The 11-day-running-mean ofβobtained from the synthetic data of EW component；（b）The 11-day-running-mean of obtained from the synthetic geomagnetic data of three components.

本文通过地磁单分量、三分量以及多台检测到的所有非均匀标度特征异常的综合分析，发现在日本东北大地震前25～50天左右以及余震期间出现的异常在多方面有基本一致的变化，相比之下，图4和图5中其他所有的异常由于仅在单台或单分量序列中出现而缺乏可信度，因此，在整个研究期间内，相对可信的异常只出现在震前25～50天左右以及余震期间，该异常现象可能反映了该地震对地磁时间序列内在的非线性系统的影响.

在目前尚难以用确定的物理模型定量解释地震前兆异常的背景下，对得到的信号异常进行统计显著性方面的检验是提高异常可信度的一种有效的方法.为了检验本文得到的震前非均匀标度特征异常是否是一种随机的频发异常，本文借鉴了统计地震学中常用的随机统计检验的思路[30］，来考察所得异常的显著性.我们通过将本文方法应用于随机合成的地磁数据的方式来进行随机统计检验.具体选取某一磁静日（例如，2011／01／09）YOK台站的地磁记录数据序列，每次生成相当于其2倍标准差的随机扰动噪声序列并与原始数据相加得到一天的随机合成数据，重复生成485次随机噪声与原始信号相加即得到485天（本文研究的时间范围）的随机合成数据，然后运用DFA方法得到随机合成数据的标度不稳定指数β和βXYZ滑动平均结果，并与YOK实际485天数据得到的β和βXYZ异常阈值标准（图4c和5c）进行比较，判断分形标度特征的异常情况，看是否会有超出阈值的情况.图6（a、b）分别为485天随机合成数据得到的β及βXYZ滑动平均结果.该模拟显示随机序列的结果并未产生如实际数据（图4，图5）显示的异常变化.我们重复进行了100次类似的随机检验，证实了类似图6的结论，即随机模拟结果均未超出实际数据的异常阈值.因此，本文得到的震前非均匀标度特征的异常变化并非由于随机扰动所致的频发异常，而是一种具有良好统计显著性的可信异常，该异常可能反映了日本东北大地震对ULF地磁信号内在的非线性系统的影响.

5 结 论

本文提出了一种能反映地磁三分量非均匀标度特征同步变化的新指标，对2011年3月11日M9.0日本东北大地震震中附近三个地磁台站16个月的ULF地磁三分量记录进行DFA处理，得到了每日地磁时间序列的分形标度特征，并提取了各分量标度特征及三分量标度特征同步变化的异常.与地震活动的对比分析表明，三个台站地磁记录的标度不稳定指数滑动平均值在强震前25～50天左右都出现了比较一致的异常增大，显示ULF地磁信号分形标度特征异常与地震活动具有较好的关联性.进一步对所得异常进行了随机统计检验，结果表明本文得到的分形标度异常并非随机扰动所致，因而具有良好的统计显著性.

致 谢 感谢两位审稿人对本文提出的宝贵意见和建议.本文所使用的HAR和YOK两个台站的地磁观测资料来自http：／／www.gsi.go.jp／ENGLISH／index.html KAK台站的观测资料来自http：／／www.kakioka-jma.go.jp.

（References）

[1]Varotsos P.The Physics of Seismic Electric Signals.Terra Pub，Tokyo，2005.

[2]Park S K，Johnston M J S， Madden T R ，et al.Electromagnetic precursors to earthquakes in the ULF band—a review of observations and mechanisms.Rev.Geophys.，1993，31：117-132.

[3]Huang Q H.Retrospective investigation of geophysical data possibly associated with the Ms8.0Wenchuan earthquake in Sichuan，China.J.Asian Earth Sci.，2011，41：421-427.

[4]Huang Q H.Rethinking earthquake-related DC-ULF electromagnetic phenomena：towards a physics-based approach.Natural Hazards and Earth System Sciences，2011，11：2941-2949.

[5]Han P，Hattori K，Huang Q，et al.Evaluation of ULF electromagnetic phenomena associated with the 2000Izu Islands earthquake swarm by wavelet transform analysis.Natural Hazards and Earth System Sciences，2011，11：965-970.

[6]Molchanov O A，Kopytenko Y A，Voronov P M，et al.Results of ULF magnetic field measurements near the epicenters of the Spitak（Ms=6.9）and Loma Prieta（Ms=7.1）earthquakes：comparative analysis.Geophys.Res.Lett.1992，19：1495-1498.

[7]Fraser-Smith A C，Bernardi A，McGill P R，et al.Lowfrequency magnetic field measurements near the epicenter of the Ms7.1Loma Prieta earthquake.Geophys.Res.Lett.，1990，17：1465-1468.

[8]Hayakawa M，Kawate R，Molchanov O A，et al.Results of ultra-low-frequency magnetic field measurements during the Guam earthquake of 8August 1993.Geophys.Res.Lett.，1996，23：241-244.

[9]Hayakawa M，Itoh T，Smirnova N.Fractal analysis of geomagnetic ULF data associated with the Guam earthquake on August 8，1993.Geophys.Res.Lett.1999，26：2797-2800.

[10]Kawate R， Molchanov O A， Hayakawa M.Ultra-low-frequency magnetic fields during the Guam earthquake of 8 August 1993and their interpretation.Phys.Earth Planet.Inter.1998，105：229-238.

[11]Du A，Huang Q，Yang S.Epicenter location by abnormal ULF electromagnetic emissions.Geophys.Res.Lett.，2002，29（10）：1455，641-643.

[12]杜爱民，周志坚，徐文耀等.新疆和田ML7.1地震前ULF电磁辐射的激发机理.地球物理学报，2004，47（5）：832-837.Du A M，Zhou Z J，Xu W Y，et al.Generation mechanisms of ULF electromagnetic emissions before the ML=7.1 earthquake at Hotan of Xinjiang.Chinese J.Geophys.（in Chinese），2004，47（5）：832-837.

[13]Zhao G Z，Zhan Y，Wang L F，et al.Electromagnetic anomaly before earthquakes measured by EM experiment.Earthquake Science，2009，22：395-402.

[14]Huang Q.One possible generation mechanism of co-seismic electric signals.Proceedings of the Japan Academy，2002，78：173-178.

[15]Ren H X，Chen X F，Huang Q H.Numerical simulation of co-seismic electromagnetic fields associated with seismic waves due to finite faulting in porous media.Geophysical Journal International.2012，188：925-944.

[16]Bak P，Tang C，Wiesenfeld K.Self-organized criticality：An explanation of 1／fnoise.Phys.Rev.Lett.，1987，59：381-384.

[17]Bak P.How Nature Works（The Science of Self-organized Critiality），Oxford University Press，1997：210.

[18]Higuchi T.Approach to an irregular time series on the basis of the fractal theory.Physica D，1988，31：277-283.

[19]Gotoh K，Hayakawa M，Smirnova N A，et al.Fractal Analysis of Seismogenic ULF Emissions.Physics and Chemistry of the Earth，2004，29：419-424.

[20]Peng C-K，Havlin S，Stanley H E，et al.Quantification of Scaling exponents and crossover phenomena in nonstationary heartbeat time series.Chaos，1995，5（1）：82-87.

[21]Peng C K，Buldyrev S V， Havlin S，et al.Mosaic organization of DNA nucleotides.Phys.Rev.，E，1994，49：1685-1689.

[22]Telesca L，Hattori K.Non-uniform scaling behavior in ultralow-frequency（ULF）earthquake-related geomagnetic signals.Physica A，2007，384：522-528.

[23]Telesca L，Balasco M，Lapenna V.Investigating the timecorrelation properties in self-potential signals recorded in a seismic area of Irpinia，southern Italy.Chaos，Solitions and Fractals，2007，32：199-211.

[24]Balasco M，Lapenna V，Romano G，et al.Extracting quantitative dynamics in Earth′s apparent resistivity time series by using the detrended fluctuation analysis.Physica A，2007，374：380-388.

[25]Telesca L，Lapenna V，Macchiato M，et al.Investigating non-uniform behavior in Ultra Low Frequency （ULF）earthquake-related geomagnetic signals.Earth and Planetary Sciences Letters，2008，268：219-224.

[26]Viswanathan G M，Peng C-K，Stanley H E，et al.Deviations from uniform power law scaling in nonstationary time scales.Phys.Rev.，E.，1997，55：845-849.

[27]黄清华，刘涛.新岛台地电场的潮汐响应与地震.地球物理学报，2006，49：1745-1754.Huang Q H，Liu T.Earthquakes and tide response of geoelectric potential field at the Niijima station.Chinese J.Geophys.，2006，49：1745-1754.

[28]黄清华，林玉峰.地震电信号选择性数值模拟及可能影响因素.地球物理学报，2010，53：535-543.Huang Q H，Lin Y F.Numerical simulation of selectivity of seismic electric signal and its possible influences.Chinese J.Geophys.（in Chinese），2010，53：535-543.

[29]Huang Q H，Lin Y F.Selectivity of seismic electric signal（SES）of the 2000Izu earthquake swarm：a 3DFEM numerical simulation model.Proceedings of the Japan Academy，2010，86：257-264.

[30]Huang Q H.Search for reliable precursors：A case study of the seismic quiescence of the 2000western Tottori prefecture earthquake.J.Geophys.Res.，2006，111：B04301.