基于断层擦痕侧伏角公式的构造应力张量反演

何 书，赵 奎，朱 忠，吴开兴

（1. 江西理工大学 资源与环境工程学院，江西 赣州341000；2. 江西理工大学 工程研究院，江西 赣州 341000）

1 引 言

在脆性变形为主的地区，变形局限于主断层带，利用断层滑动资料可以反演断层所在地区的构造应力张量[1]。自从Bott首次提出利用断层擦痕反演应力张量的基本原理以来，利用断层擦痕资料反演构造应力场的方法及其应用在国内外得到了迅猛发展[2－10]。Aleksandrowski利用 Bott推导的公式计算出在不同应力比率条件下若干个断层面上擦痕的侧伏角，以此提出了利用断层擦痕资料确定主应力方向的图示方法[11]。张银旗等[11]利用空间解析几何方法证明了Aleksandrowski的图示法适用于任何应力状态和各向异性岩石，并能准确的确定主应力方位。在实际应用中，Etchecopar等[5]提出的演算应力张量的反演技术最为普及，简称EC法。EC法原理较为简单，但计算过程略显复杂。Aleksandrowski提出的断层擦痕侧伏角公式反映的是侧伏角与应力比值及主应力之间的关系，其目的主要是为了解释图示法求解构造主应力方向的正确性。笔者将应用于图示法的公式与传统反演法的基本原理相结合，利用最小二乘法，将两种方法统一起来，改进了原有反演法的求解过程，使得计算过程更加简单明了，易于实现。在此基础上，通过对江西武山铜矿北矿带断层滑动特征的观测分析，将改进后的反演法应用于该地区的构造应力主方向研究中，并与震源机制解方法获得的现代构造应力场结果进行对比，获得了满意的结果。

2 研究方法及公式推导

2.1 反演法的基本原理

反演法应用的基本前提是，在区域构造应力场作用下, 岩层中已存在或新产生断层的滑动方向与断面上剪切应力方向一致。基于以上前提，该方法利用弹性力学的方法，根据断层面产状计算剪应力方向，然后与断层面上的擦痕方向进行非线性最小二乘法拟合，以求得某一断层在活动时期的3个构造主方向和 1个主应力差之比 R（ (σ2-σ3)/(σ1-σ3)）。该方法要求参与计算的擦痕必须是同一期构造应力下形成的。

2.2 基于断层擦痕侧伏角公式的构造应力主方向求解过程

根据弹性力学的相关理论，一点的应力状态可由张量T表示，在主应力参考系中张量T可表示为

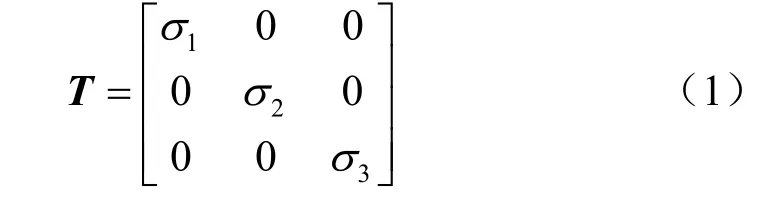
应力张量T的确定需建立两套坐标系来完成，一套是主应力方向坐标系；另一套是地理坐标系x,y, z（其中x轴正方向为正东方向，y轴正方向为正北方向，z轴则朝上）。两套坐标系之间的关系可用3个欧拉角（φ, θ, φ）（分别表示两套坐标系对应坐标轴的夹角）来表示（见图1）。

为了探讨断层面上擦痕与主应力之间的关系，在前人研究基础上，Aleksandrowski[11]推导的侧伏角计算公式为

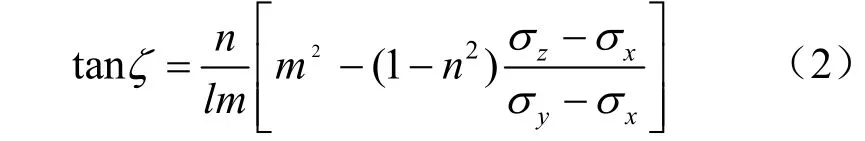
式中：ζ为擦痕的侧伏角；σx、σy和σz分别为与坐标轴一致的主应力；l、m和n为在主应力坐标系下断层面法线方向余弦。

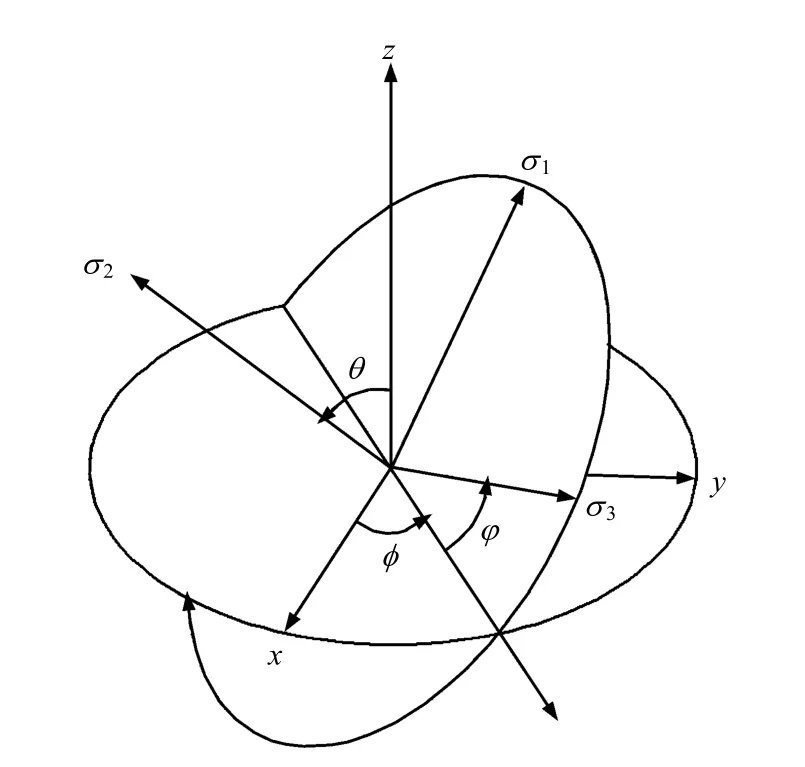
图1 欧拉角与主应力方向及地理坐标系的关系Fig.1 The relation between Euler angles and principal stress direction and geographic coordinate system

假设 σz=σ2， σy=σ1， σx=σ3，令R= (σ2- σ3)/(σ1- σ3)，则式（2）可变为

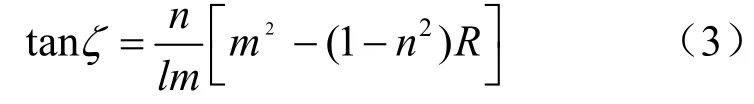
在此，若已知一系列同期构造应力场作用下形成的断层面产状及主应力方向，即可通过坐标变换求得式（3）中的l、m和n。由于主应力方向及大小都是未知的，于是式（3）含有 4个未知数：（φ, θ, φ，R）。若要求解这4个未知数，必须求解一个非线性方程组，且断层面的个数必须大于等于4个。

设在地理坐标系统中断层面都是通过坐标原点的，则倾角为α，倾向为β的断层面的向上单位法线矢量可表示为

式中： A = sin αsin β， B=sin αcos β，C=cosα

若已知3个欧拉角为φ、θ、φ，则断层面在主应力坐标系中的单位法向矢量nˆ′可由下式求解：

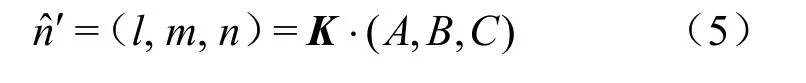
其中K为方向余弦矩阵：

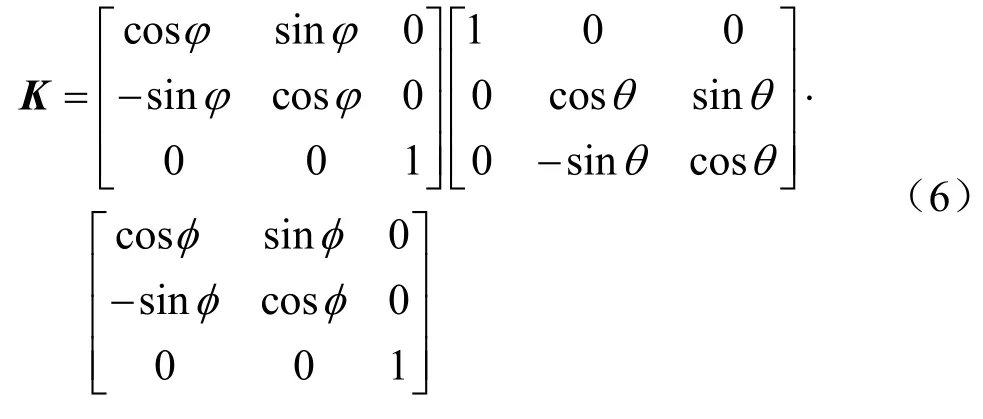
求解过程中，首先要产生一个随机均匀分布的（φ, θ, φ，R）4个未知数的初值，其中φ，φ在0到2π中取值，θ在0到π中取值，R在0到1中取值。然后将这4个初值及一系列断层面产状数据代入式（3）中，可得到一个非线性方程组，然后根据数值方法求解。据反演方法的假设，求解该方程组的目的即为求解理论擦痕侧伏角与实际测量的擦痕侧伏角之间的夹角最小。这是一个非线性的最小二乘拟合问题，可表示为

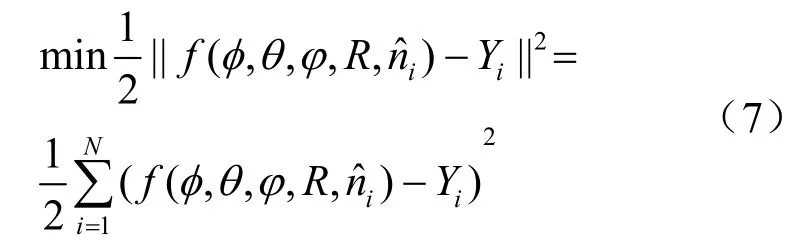
函数 f( φ,θ,φ, R,ni)由式（3）求解：

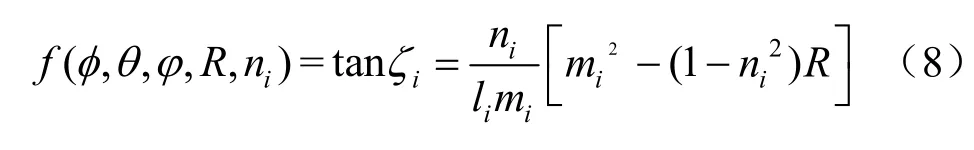
根据已知的断层擦痕及断层面数据，求解一个非线性最小二乘法拟合问题，可求出4个未知数：(φ, θ, φ，R)，从而确定主应力方向。以上求解过程可利用Matlab软件编制程序完成，其过程较易实现。

3 应用实例

3.1 研究区概况

笔者选取位于江西瑞昌县境内的武山铜矿区，开展了井下断层滑动特征的调查，对相关数据进行了详细测量。武山铜矿区位于九瑞矿田中部，横立山-黄桥向斜东段北翼，据矿体控制因素及空间展布特征，将该矿床以二叠系栖霞阶地层上限为界划分为南、北两个矿带。武山铜矿区自晚白垩世以来，主要发育一系列北北西向断裂，横切矿区北矿带（见图2）。根据这些断层的平面展布特征及其与地层的切割关系，可推断属于同一期构造作用的结果。现场调查表明，北西向断裂伴随硅质、铁质胶结与破碎构造角砾岩的产出,多为高倾角断层，倾伏角很小，滑动方向近于水平，属于典型的走滑断裂。这些断层横切矿区矿体，研究这些断层所反映的构造应力特征，对矿山采矿巷道布置及其稳定性的分析有着重要意义。

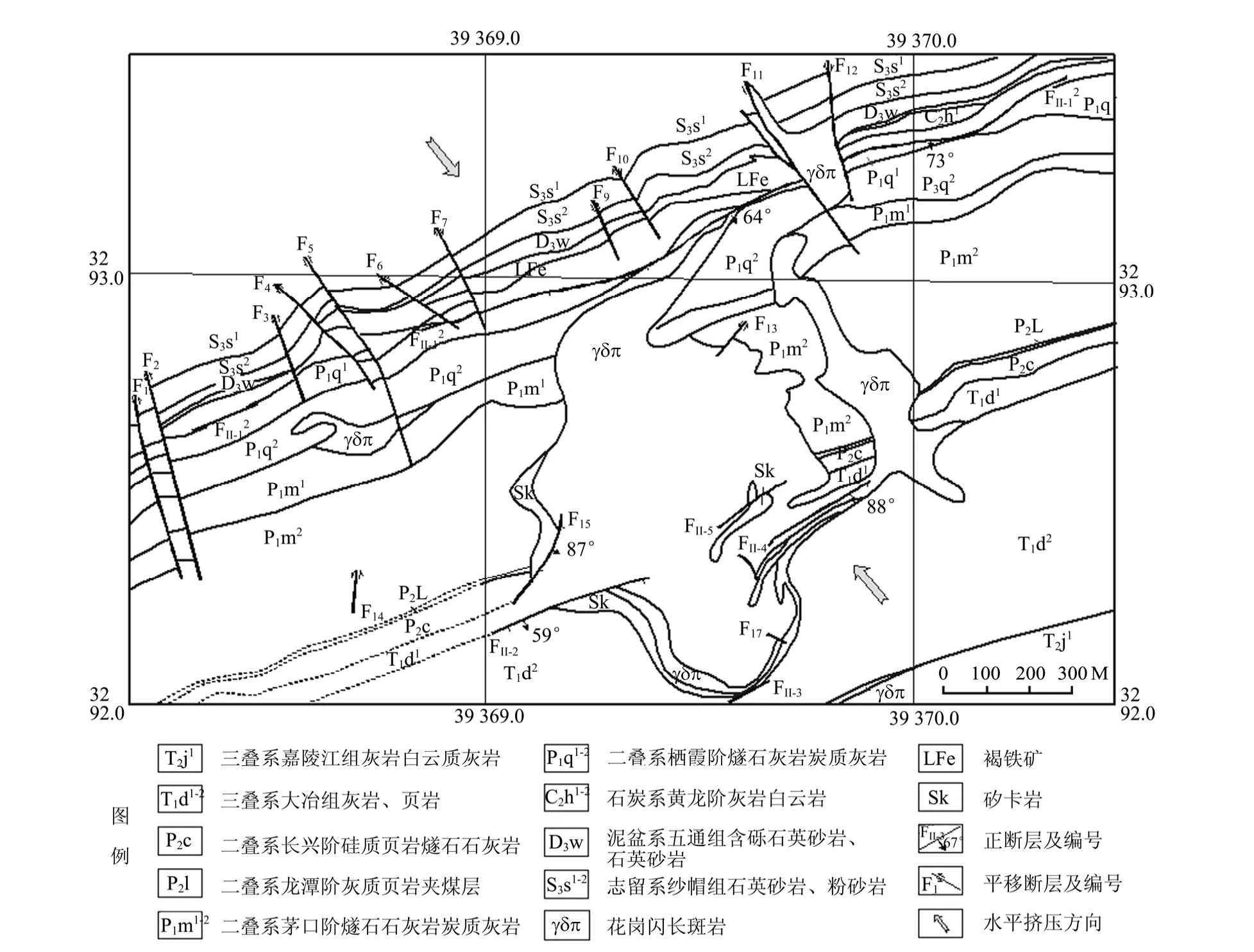
图2 武山矿区断裂分布图Fig.2 The distribution of faults in the Wushan mining region

3.2 断层滑动资料观测及计算结果分析

对矿区北矿带井巷工程揭露的 11条北北西向断层进行了实地观测（见表1），获得了反映断层滑动的特征数据。现场调查结果表明，断层擦痕的倾伏向与断层走向近于一致，倾伏角接近于 0，在利用改进的构造应力张量反演方法中，式（7）中的实测擦痕Yi皆等于0，运算过程变得更加简单。经过反复改变参数，得到了该区的构造应力主方向（见表2）。计算结果显示，最大主应力倾伏向为336°；中间主应力的倾伏角为 59°；最小主应力倾伏角仅2°，方向近于水平。实测走滑断裂发育于横立山-黄桥向斜的北翼，该向斜轴面呈北东-南西向展布，是该地区地层受到北西-南东向水平挤压构造应力作用的结果（见图2）。将上述计算结果与区域构造水平挤压方向对比分析不难看出，两者具有一定的相似性，说明该区受来自北西-南东向的水平挤压具有持续性的特点。以上分析表明，本区构造应力主方向的计算结果与走滑断裂所在地质构造背景基本吻合，说明反演成果是可信的。

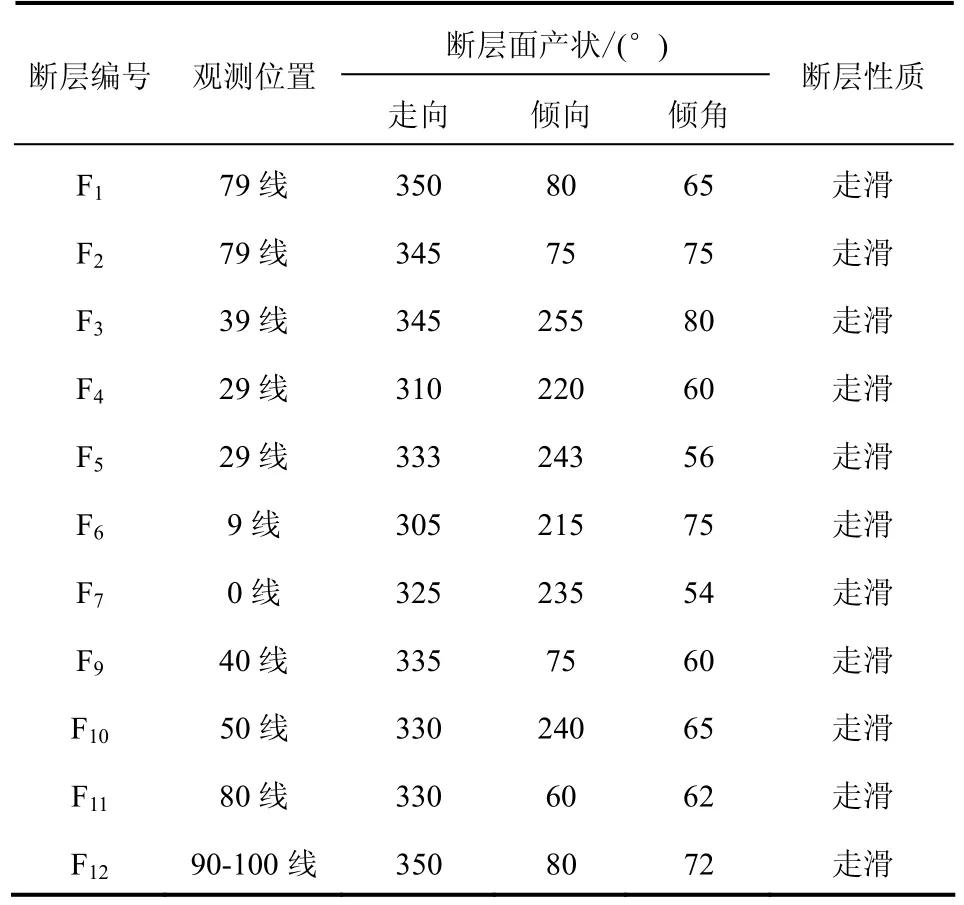
表1 断层观测数据表Table 1 The observed data of faults

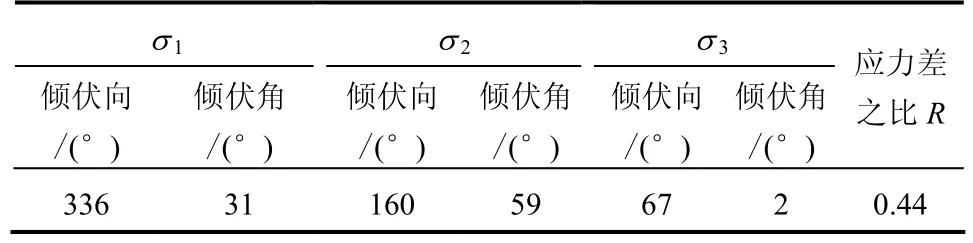
表2 主应力方向计算结果Table 2 The calculated results of principal stress direction

3.3 与震源机制解的对比分析

研究区最近的一次地震活动为2005年11月26日发生的九江-瑞昌5.7级地震和4.8级强余震。王墩等[12]对九江-瑞昌地震的发震构造研究认为，地震活动主要是在近东西向挤压应力场作用下，瑞昌断裂产生右旋逆冲走滑运动，同时牵动引发了与其交汇的北西向武山隐伏断裂的错动，使其产生左旋滑动，两组断裂共轭剪切作用形成了此次地震北西向武山隐伏断裂错动的结果。研究表明，武山铜矿区出露的北北西向断裂与武山深部隐伏断裂密切相关，是隐伏断裂在地壳表层的一种表现。从对地貌的控制来看，断裂在新构造期活动较为明显。因此，这些断层的错动特征与现代构造应力场具有一定联系。根据震源机制解，构造应力场主压应力方向在287°～297°之间，武山铜矿所在地区现代构造应力场呈现北西-南东向挤压的主要特征。对比震源机制解和依据走滑断裂滑动资料的反演成果，表明两种方法计算的构造应力主方向近于一致，反映了武山铜矿区受北西-南东向挤压的构造应力场特征，表明该区现代构造应力场与古构造应力场之间有着密切的关系。

4 结 论

（1）基于Aleksandrowski提出的侧伏角计算公式和最小二乘拟合法，结合EC构造应力张量反演的基本原理，提出了改进的构造应力张量反演方法。

（2）在实测武山铜矿区断层滑动资料的基础上，利用改进的反演方法，得出了矿区现代构造应力场的3个主应力方向。计算过程表明，改进的反演方法计算过程更加简单，容易实现，计算结果比较符合实际。

（3）将反演结果与最新的震源机制解结果对比分析表明，两种方法计算的构造应力主方向近于一致，表明武山矿区的构造应力场特征具有一定的稳定性，该区现代构造应力场与古构造应力场之间有着密切关系。

[1]吴树仁. 利用断层滑动资料反演构造应力场的方法[J].地质科技情报, 1990, 9(3): 95－100.WU Shu-ren. The inverse techniques of tectonic stress fields using fault slip data[J]. Geological Science and Technology Information, 1990, 9(3): 95－100.

[2]BOTT M H P. The mechanism of oblique slip faulting[J].Geological Magazine, 1959, 96(2): 10－14.

[3]ANGELIER J. Determination of the mean principal directions of stresses for a given fault population[J].Tectonophysics, 1979, (56): 17－26.

[4]ANGELIER J. From orientation to magnitudes in paleostress determinations using fault slip data[J].Journal of Structural Geology, 1989, 11 (1－2): 37－50.

[5]ETCHECOPAR A, VASSEUR G, DAIGNIERES M. An inverse problem in microtectonics for the determination of stress tensors from fault striation analysis[J]. Journal of Structural Geology, 1981, 3 (1): 51－65.

[6]谢富仁, 苏刚, 崔效锋, 等. 滇西南地区现代构造应力场分析[J]. 地震学报, 2001, 23(1): 17－23.XIE Fu-ren, SU Gang, CUI Xiao-feng, et al. Modern tectonic stress field in southwestern Yunnan, China[J].Acta Seismologica Sinica, 2001, 23(1): 17－23.

[7]荆振杰, 杜义, 谢富仁. 昆明周边地区活动断层滑动与现代构造应力场[J]. 地震学报, 2008, 30(3): 230－239.JING Zhen-jie, DU Yi, XIE Fu-ren. Contemporary tectonic stress in Kunming basin and surrounding regions deduced from fault slip in version[J]. Acta Seismologica Sinica, 2008, 30(3): 230－239.

[8]陈正乐, 杨农, 王平安, 等. 江西临川地区相山铀矿田构造应力场分析[J]. 地质通报2011, 30(4): 514－531.CHEN Zheng-le, YANG Nong, WANG Ping-an, et al.Analysis of the tectonic stress field in the Xiangshan uranium ore field, Linchuan area, Jiangxi, China[J].Geological Bulletin of China, 2011, 30(4): 514－531.

[9]司荣军, 王春秋, 程国强. 大安山矿后槽构造应力场数值模拟研究[J]. 岩土力学, 2006, 27(增刊1): 167－170.SI Rong-jun, WANG Chun-qiu, CHENG Guo-qiang.Numerical simulation study of tectonic stress field of Houcao area in Daanshan Coal Mine[J]. Rock and Soil Mechanics, 2006, 27(Supp.1): 167－170.

[10]杨树新, 陈连旺, 谢富仁. 中国大陆现今构造应力场的回归分析研究[J]. 岩土力学, 2003, (增刊2): 357－360.YANG Shu-xin, CHEN Lian-wang, XIE Fu-ren. A study of regression analysis and numerical simulation on modern tec-stress field in China mainland[J]. Rock and Soil Mechanics, 2003, (Supp.2): 357－360.

[11]张银旗, 何绍勋, 段嘉瑞. 根据断层擦痕确定主应力方位理论及方法的探讨[J]. 地质与勘探, 1992, 28(8): 35－42.ZHANG Yin-qi, HE Shao-xun, DUAN Jia-rui. On the method for determination of principal stress from fault slickenside[J]. Geology And Prospecting, 1992, 28 (8):35－42.

[12]王墩, 肖和平, 姚运生, 等. 九江-瑞昌地震序列的构造背景与发震构造探讨[J]. 大地测量与地球动力学,2007, 27(增刊 1): 15－21.WANG Dun, XIAO He-ping, YAO Yun-sheng, et al. On seismogenic and its background tectonics of Jiujang-Ruichang seismic sequence[J]. Journal of Geodesy and Geodynamics, 2007, 27(Supp.1): 15－21.