拱形结构爆炸作用荷载分布规律研究

洪 武 ，周健南，徐 迎，金丰年，范华林

（1. 兰州交通大学 甘肃省道路桥梁与地下工程重点实验室，兰州 730070；2. 解放军理工大学 爆炸冲击防灾减灾国家重点实验室，南京 210007；3. 重庆交通大学 （桥梁）结构工程重点实验室，重庆 400074；4. 河海大学 岩土力学与堤坝工程教育部实验室，南京 210098）

1 引 言

爆炸条件下大跨度洞库结构荷载分布规律的研究是大跨度洞库结构设计计算方法的基础。目前主要有两种方法确定爆炸作用下地下结构上的荷载。一是TM5-855-1手册中提出的方法[1]，其思路是：作用在结构上的荷载是一个用常系数扩大了的自由场压力荷载。该方法未考虑介质与结构的相互作用。二是以美国空军防护结构设计手册(PCDM)提供的方法为代表[2]，该方法考虑介质与结构相互作用，在一定的假设条件下利用介质与结构相互作用理论得出作用到结构上的荷载。

前者简单实用，多数情况下能够满足工程需要。但对于柱壳结构的地下大跨度结构而言，由于常规武器爆炸的压缩波为球面波，波与结构相互作用变得复杂，常系数如何确定需进一步研究，这就使得研究自由场结构上荷载的分布规律存在一定难度。

孙博[3]对大跨度结构在不同爆炸距离、不同结构跨度下的自由场地冲击应力的变化和分布规律进行了研究，研究结论表明，拱顶爆炸时作用在拱上的荷载具有一定的分布范围，荷载作用范围随跨度的增大而减小，证明结构的跨度、曲率对作用在结构上的荷载范围有着显著的影响；当非拱顶爆炸时，只是随着爆源相对拱结构的偏角位置变化而偏移，而分布规律一致，并给出了基于自由场的考虑偏离拱顶爆炸时拱顶任意点的最大应力值计算公式。范俊余等[4]采用数值计算对地面爆炸作用下浅地表波场的分布以及土中浅埋结构上的荷载进行了分析。

自由场峰值应力计算方法主要有美国陆军防常规武器设计手册TM5-855-1的计算公式[1]、美国应用研究所 Drake计算公式[5]、美国西南研究所Westine 计算公式[6]、俄罗斯 пяхоъ 计算公式[7]及基于试验的经验拟合公式[8－9]等。由于TM5-855-1公式能够反映不同介质中的耦合效应、不同介质波传播特性差别以及地冲击衰减的差别，使用范围较广，是较常用的自由场峰值应力计算公式。本文采用该公式进行理论计算：

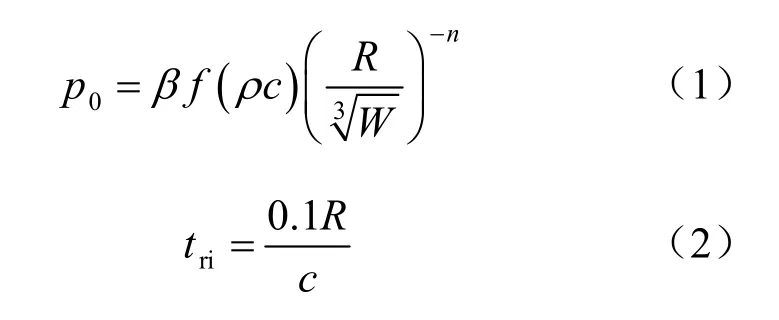
式中：p0为峰值应力（MPa）；β为系数（与介质材料有关），取 0.47；f为耦合系数；ρ为介质密度（kg/m3）；c 为波速（m/s）；(ρc)为介质材料的声阻抗（MPa·s/m）；R为装药距所求点的距离（m）；W为装药重量（N）；n为衰减系数；tri为压缩波升压时间（s）。

实际洞库工程跨度一般较大，本文针对跨度24～50 m；爆高3～30 m及不同TNT当量工况进行计算分析，具体参数如表1所示，示意图如图1所示。

表1 计算模型跨度和圆弧拱半径表 (矢跨比为1/5)Table 1 Values of span and radius of arches

图1中爆心离圆弧拱顶点垂直距离为H，爆心与圆弧环向各点的距离为r，根据几何关系得到：

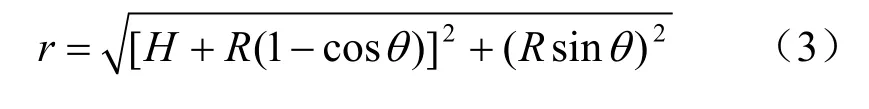
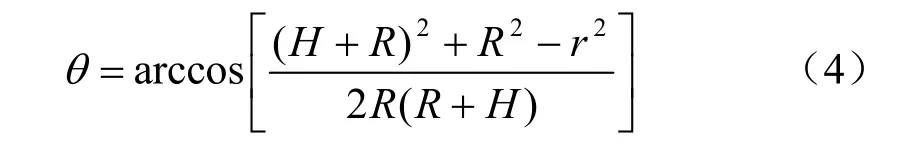
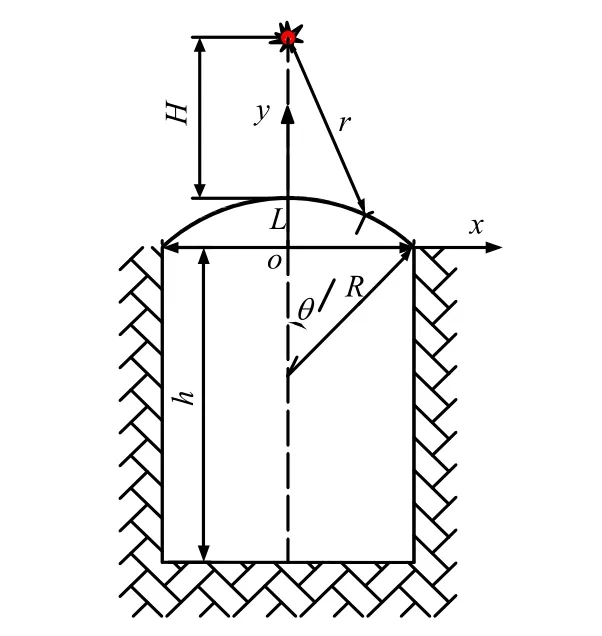
图1 模拟工况示意图Fig.1 Sketch of simulated condition

2 数值计算模型

2.1 参数选择及模型建立

本文采用有限元分析软件[10]进行数值计算，岩石介质与拱形结构均采用塑性动力学模型(PLASTIC KINEMATIC)模拟，具体参数如表 2所示。岩石介质在计算中简化为各向同性均匀介质，为了尽量减少计算工作量，取通过球形装药中心面将模型简化为1/2平面模型，同时为了减小边界效应对计算结果的影响，在底边和侧边等非对称边界设置了透射边界。为更好地反映材料几何大变形和失效等非线性问题，计算采用单点积分和沙漏控制。

炸药用HIGH EXPLOSIVE BURN材料模型和JWL状态方程来模拟，其材料参数见表3，其中A、B、R1、R2及ω为 JWL炸药方程系数，E0为初始内能，D为爆速。建模过程中采用初始化体积的方法建立炸药；24 m跨工况计算模型设置如图2所示。

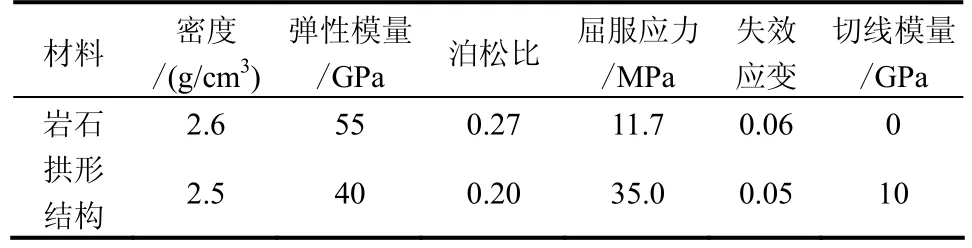
表2 岩石介质材料模型参数Table 2 Parameters of rocks

表3 炸药材料参数Table 3 Parameters of TNT

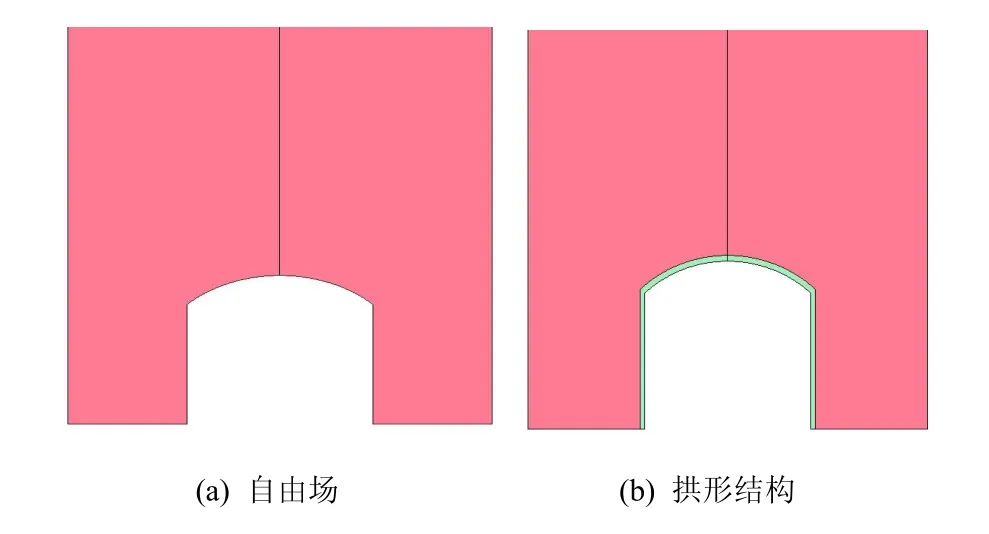
图2 数值计算模型图（跨度24 m，爆高10.5 m）Fig.2 Numerical models (the arch with a span of 24 m and an explosion distance of 10.5 m)

2.2 计算结果验证

将TM5-855-1公式计算和数值计算结果进行对比，将式（1）转化为国际单位制则变为式（5），计算中β=0.47， f=1。

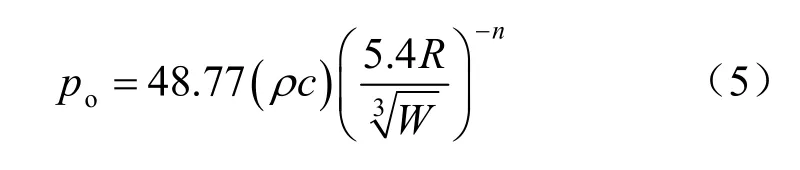
图3对数值计算和理论计算结果进行了对比，可以看出，数值计算和理论计算结果吻合较好，说明数值计算参数选取合理，计算结果具有较高的可信度。

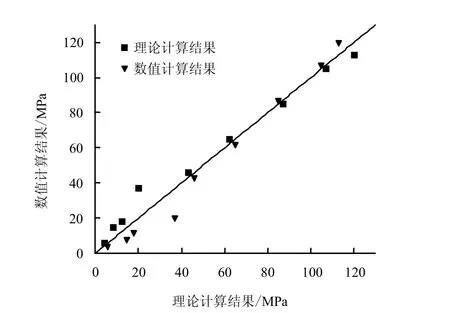
图3 数值计算结果和理论计算结果对比Fig.3 Comparisons between numerical and theoretical results

3 爆炸荷载的分布规律

图4给出了地下爆炸产生的应力波作用于大跨度洞库结构过程的应力云图，爆炸产生的球形波首先作用于拱顶，随后沿着拱形向拱脚传播，当应力波达到拱脚后继续传播，会在拱脚处绕射，绕射的应力波作用于大跨度洞库结构的边墙上。

图5给出了不同角度θ达到峰值应力时刻，拱结构自由面上应力峰值的分布曲线，可以看出，拱顶首先达到最大值，t=H/v，v为爆炸应力波的波速，随后峰值逐渐沿着拱形自由面传播，在初始很短时间内，拱顶应力峰值大于等于拱上其他位置应力峰值，拱形自由面上应力峰值分布曲线呈现“近似三角形”；但随着应力波向拱脚的传播，拱顶的应力峰值逐渐变小，拱上应力峰值分布曲线呈现“马鞍形”，曲线的最大应力峰值始终小于拱顶的最大应力峰值，且仍不断减小。所有不同时刻应力峰值曲线的外包包络线即为地下爆炸时拱形洞库结构自由面上最大应力峰值分布曲线。

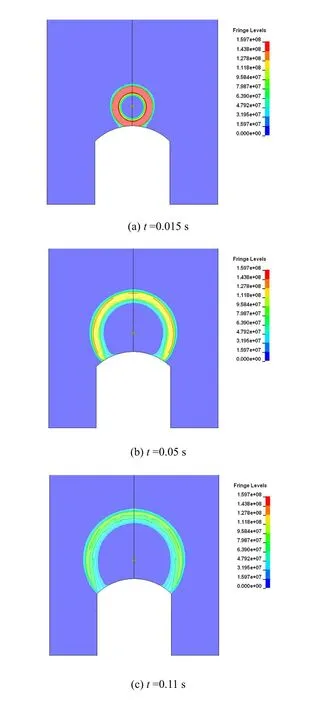
图4 地下爆炸作用于大跨度洞库自由场应力云图(跨度24 m，爆高10.5 m)Fig.4 Stress nephograms of free field arch impacted by underground explosion (with a span of 24 m and an explosion distance of 10.5 m)

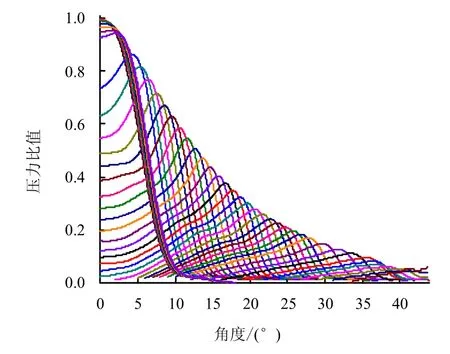
图5 不同时刻拱上应力峰值分布曲线（跨度24 m，爆高10.5 m）Fig.5 Curves of peak stress on arch at different times(with a span of 24 m and an explosion distance of 10.5 m)

拱形自由面上的应力峰值分布规律随着爆高及跨度的变化规律如图6所示，图中对应力峰值进行了归一化处理。不同爆高时拱形自由面上应力峰值的分布规律呈近似“三角形”分布，拱顶最大，并向拱脚衰减，但不同的爆高，应力峰值的衰减幅度及速率不同。随着爆高的增加，尽管作用于拱形自由面上的应力峰值的绝对值因爆距增加而减小，但相对应力峰值会随着爆高的增加而增加，这种增加的幅度随着距离拱顶的角度的增加而提高，即随着爆高的提高，拱形自由面上应力分布越趋于均匀，例如当爆高为3.0 m时，40°对应的拱形自由面上相对应力峰值为0.07，而爆高为30.5 m时，相对应力峰值为0.298。图6给出的拱形自由面上应力峰值随跨度分布规律表明，随着跨度的增加而趋于集中，随着跨度的减小趋于均匀，例如当跨度为50 m时，40°处拱形自由面上的相对应力峰值为 0.031，而跨度为24 m时相对应力峰值为0.169；当矢跨比等于1/5时，θ的值为-44°～44°，但无论在那种工况下，拱形自由面上均具有应力，这和TM5-855-1认为应力有一定的作用范围，并不是满跨作用[1]，存在一定的出入，当然，在某些工况下，接近拱脚部分的应力相对较小，可近似忽略。

拱结构上每一点处的应力峰值都不一样。图 6给出了拱形自由面上应力峰值随着角度θ的变化曲线f(θ)，同时曲线还受到爆高及拱结构跨度的影响，则可以得到应力峰值在拱结构上的分布规律曲线f(θ,κ)，其中κ= H/R 。因此，拱形自由面上应力峰值的表达式为

式中：p为拱形自由面上应力峰值；po为拱顶的应力峰值；f(θ,κ)为应力峰值分布函数。

通过对图6的分析得到f(θ,κ)函数的表达式：

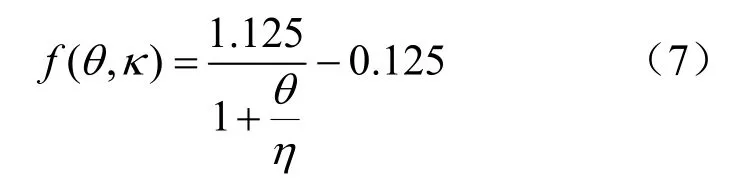
式中：η = (39 - 44.5e-κ/0.28)1.7为大跨度结构爆高/跨度系数；θ为计算位置与拱顶夹角，θ＞0°。

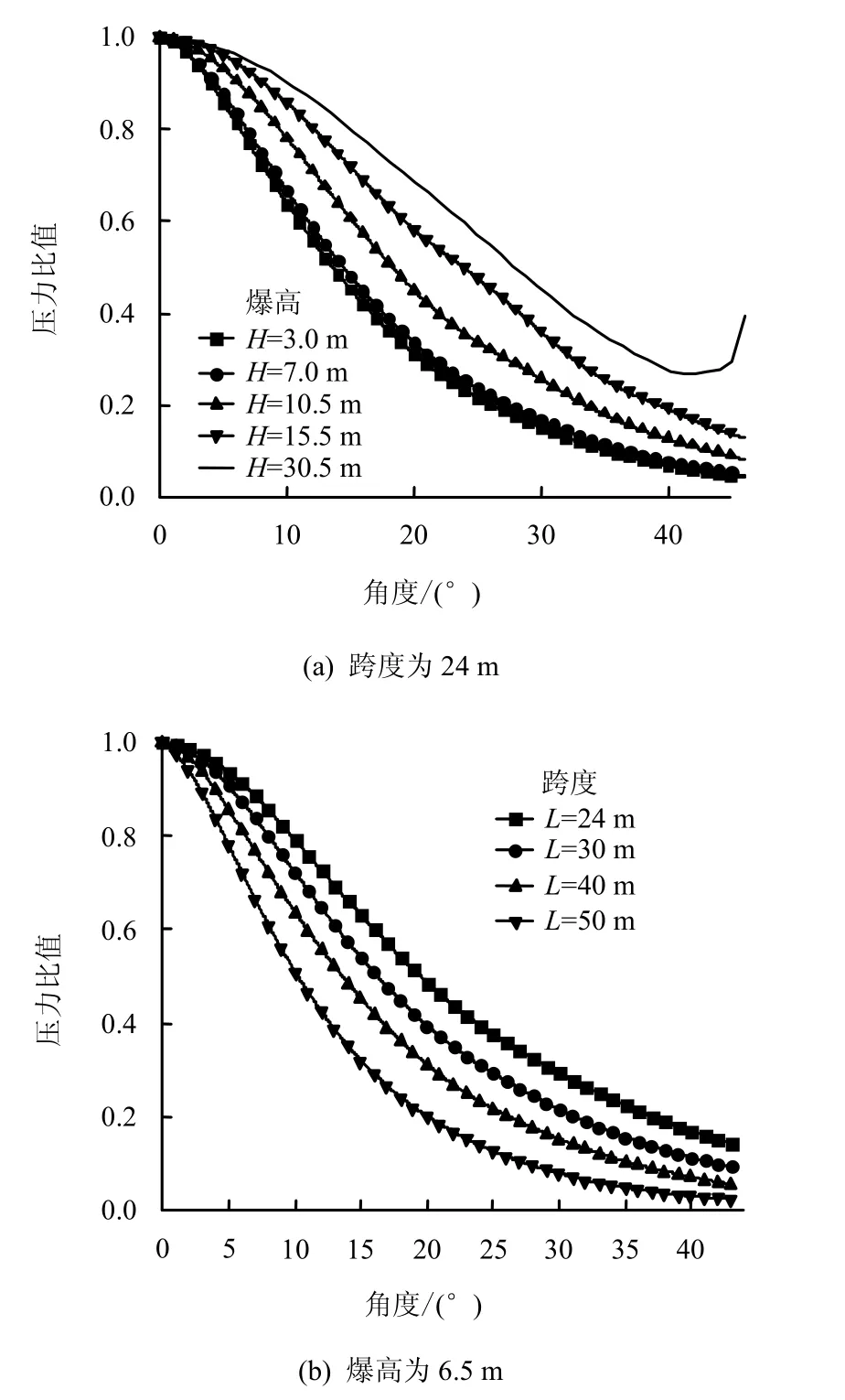
图6 不同爆高、跨度拱上应力峰值分布曲线Fig.6 Peak stresses on arch at different explosion distances and different spans

图7对不同H/L情况下的计算结果和式（7）的计算结果进行了对比。可以看出，当H/L ＜0.369时，数值计算结果与式（7）的计算结果能够很好吻合，当H/L ＞0.369时，两者计算结果存在一定的差别，当θ＞25°时，式（7）和数值计算结果开始出现偏差，在接近拱脚位置（44°），这种误差可以达到约20%，但考虑到拱脚应力相对于拱顶应力比较小，因此，式（7）还是具有较好的工程应用价值。

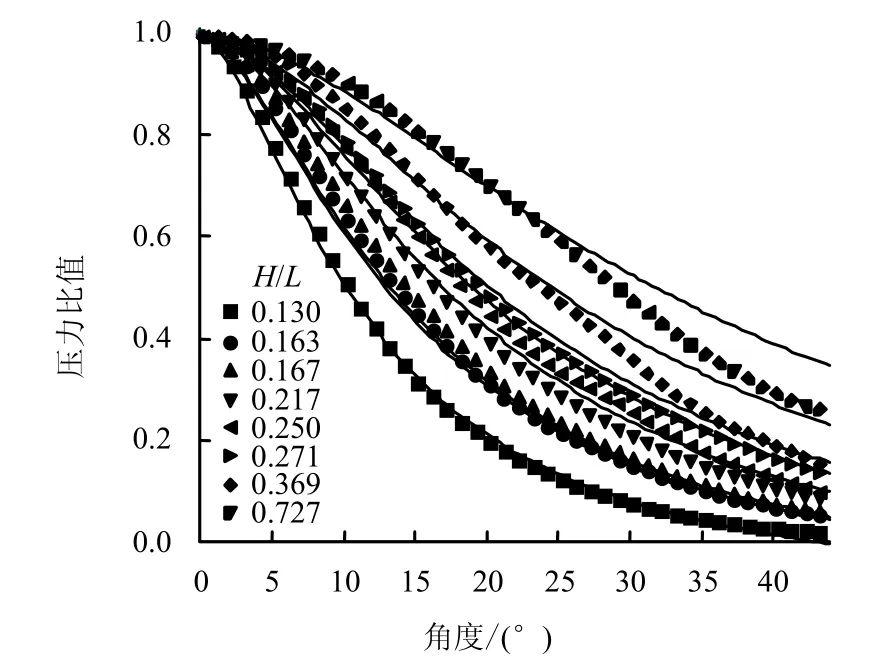
图7 拟合公式与数值计算结果对比Fig.7 Comparison between fitted equation and numerical calculation

目前，现有文献对于钻地爆作用下地下大跨度洞库边墙的应力分布情况研究较少，但当大跨度结构的边墙较高时，即高边墙、大跨度拱结构，边墙的稳定性对于结构的安全就变得非常重要。本文对大跨度结构边墙的应力峰值分布规律也进行了研究，图8给出了类似图5的不同时刻时作用在边墙上的应力峰值分布曲线，当爆炸应力波作用于边墙顶部，即边墙与拱脚衔接处时，边墙顶部的应力峰值最大，而沿着边墙迅速衰减，且应力峰值作用范围非常小，例如此时边墙顶部应力峰值为33.5 MPa，而距离顶部为2.3 m处的应力峰值仅为1.13 MPa；随着时间的推移，绕射过拱脚的应力波作用于边墙，使得边墙上应力分布的范围越来越大，但应力峰值的强度明显减小，且作用于边墙上的应力峰值分布曲线变化规律并不一致，而是呈现波浪形，图8中不同位置应力峰值包络曲线显示应力峰值随着边墙高度的降低，强度减小且趋向均匀。

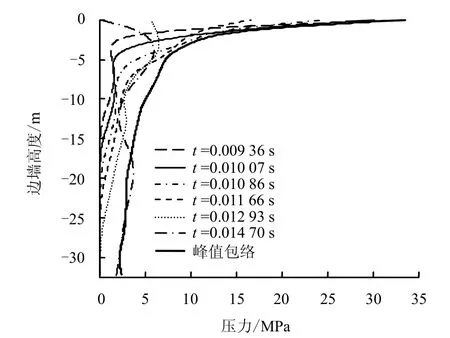
图8 同时刻边墙荷载分布曲线（跨度24 m，爆高6.5 m）Fig.8 Load curves on side-wall (with a span of 24 m and an explosion distance of 6.5 m)

图9分别给出了边墙应力峰值（采用拱顶荷载峰值进行归一化）在不同爆高、跨度情况下沿着边墙的分布曲线。图 9(a)显示，随着爆高的增加，作用在边墙的应力峰值随之增大。不同爆高情况下，沿着边墙的应力峰值近似可以分为两部分，边墙顶部至距顶部2.5 m处为应力峰值的衰减段，应力峰值近似呈线性衰减，从距离顶部2.5 m处向下，应力峰值近似均匀分布。从图9(b)中可以看出，应力峰值沿着墙体高度从墙体顶部快速衰减，与图9(a)相似，曲线也可以分为衰减段和近似均匀段两部分。随着跨度的增加，作用在边墙的应力峰值减小。通过对图9的分析，可以给出在不同爆高、跨度情况下，应力峰值沿着边墙高度分布的计算公式为

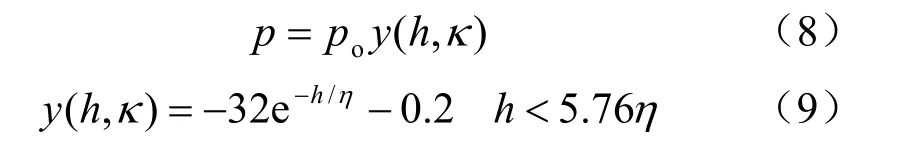
式中：y(h,κ)为应力峰值沿边墙分布系数；η=0.001 5κ-1.5为H/L影响系数。

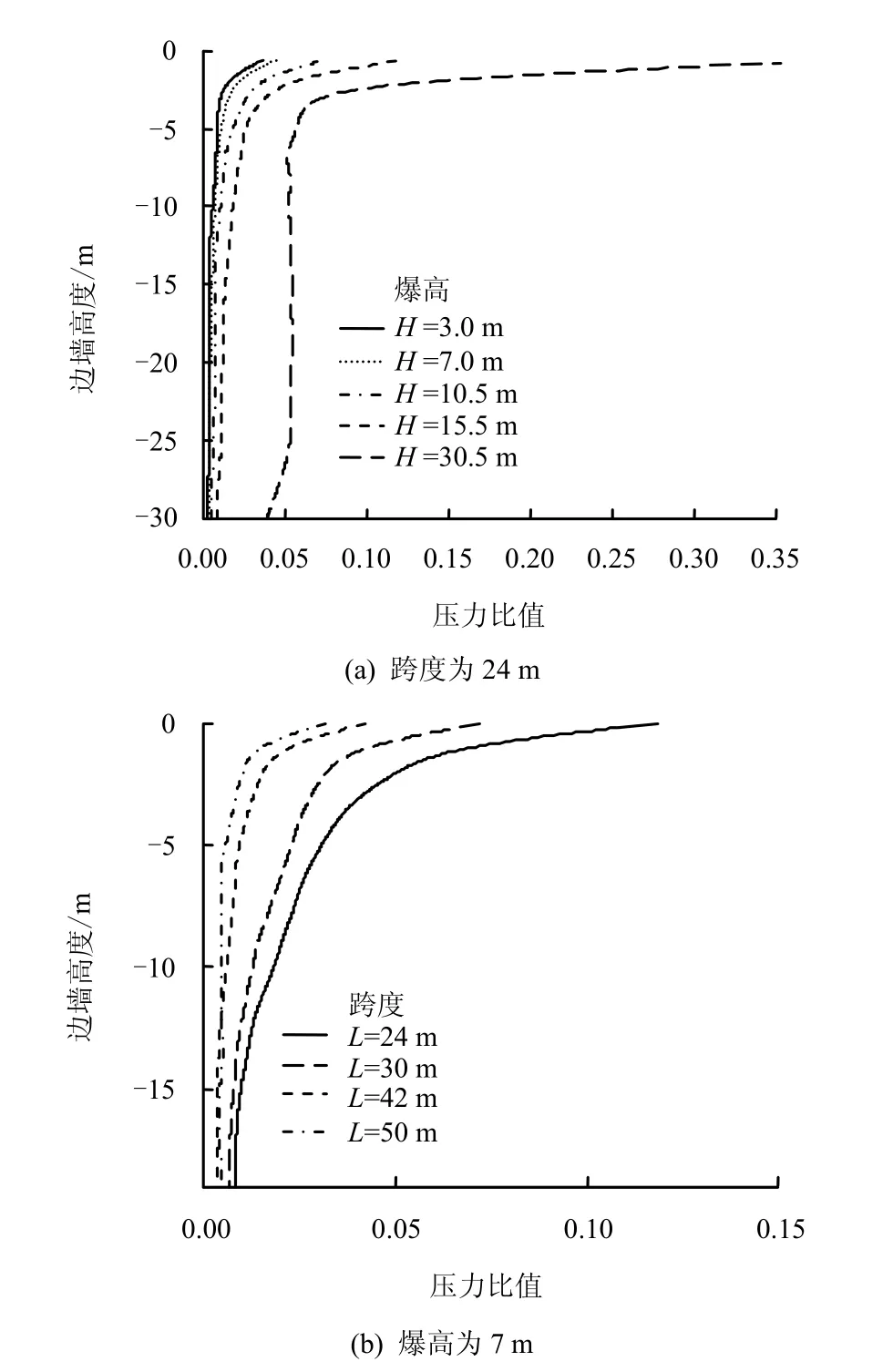
图9 不同爆高、跨度拱上应力峰值分布曲线Fig.9 Peak stresses on side-wall at different explosion distances and different spans

图10对不同H/L情况下的计算结果和式（8）的计算结果进行了对比，当边墙高度距拱脚大于1 m时，数值计算结果与式（8）的计算结果吻合较好，但当边墙高度距拱脚小于1 m时，即非常靠近边墙和拱形交接处时两者存在很大的误差，这是因为爆炸应力波在此处出现绕射、湍流等复杂现象，使得这一部位的应力峰值情况较为复杂，因此，式（8）的应用范围应该受到一定的限制，在计算接近拱脚处边墙应力峰值时可以参考式（7）的计算结果。

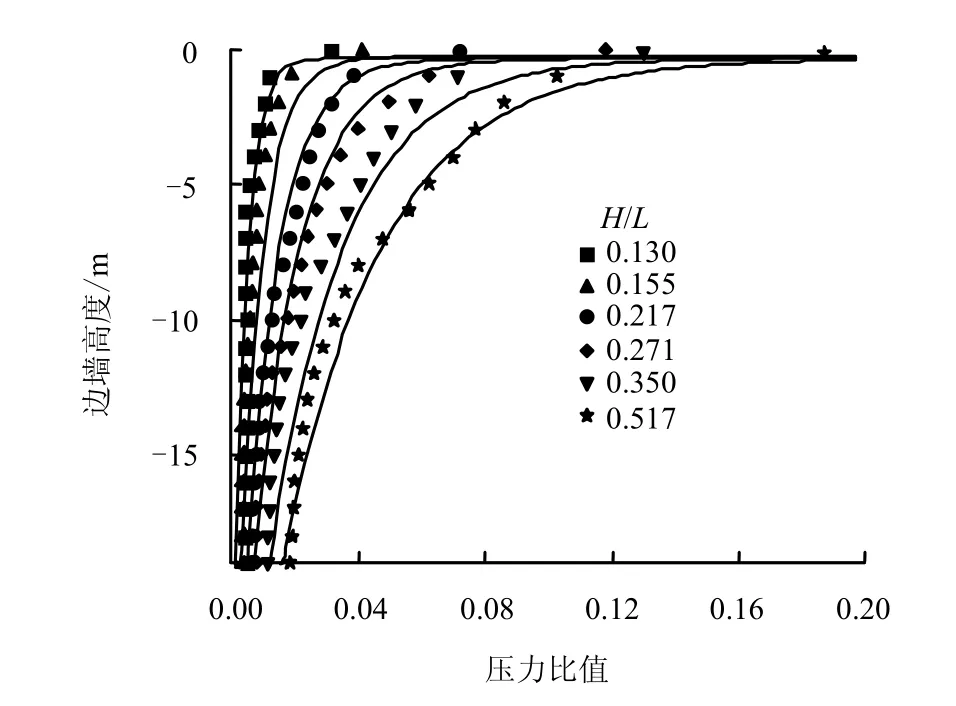
图10 拟合公式与数值计算结果对比Fig.10 Comparison between fitted equation and numerical calculation

4 荷载系数分布规律

TM5-855-1[1]提出：自由场应力沿着反射路径的数值乘以荷载系数就可以确定作用在结构上的荷载，并在试验数据基础上提出采用1.5的荷载系数可以基本满足工程需要，但这一结论是通过平面反射试验数据获得的，与地下大跨度拱形结构存在较大的差别，因此，有必要对大跨度拱形结构上的应力波荷载系数进行研究。图11给出了爆高为7 m不同跨度情况时荷载系数在拱结构上的分布曲线。爆炸应力波在拱顶的荷载系数最小，而且由于爆高不变，不同跨度情况下拱顶位置的荷载系数基本不变，约为1.5～1.7，这与TM5-855-1[1]给出的数值吻合。随着拱形偏心角θ的增加，荷载系数沿着拱形不断增大。随着跨度的增加，增加的幅度越明显，原因在于当爆高不变时，随着跨度的增加，应力波的入射角越来越小，因此，反射也越来越强烈。

图12给出了跨度为30 m时不同爆高情况下的荷载系数分布情况，应力波在拱顶的荷载系数基本保持不变，约为1.5～1.7，能与TM5-855-1[1]吻合，正荷载系数不随入射强度发生变化。随着拱形偏心角的增加，荷载系数不断增大，但是增加的幅度随爆高的增加而减缓，当爆高为3.5 m时，拱顶和拱形偏心角39°处有明显的差别，而当爆高为15.5 m时，荷载系数随拱形偏心角的变化已经非常模糊了。当跨度不变时，随着爆高的增加，作用在拱形结构上应力波的入射角差别越来越小，因此，荷载系数也趋于一致。拱形结构上荷载系数的计算公式为

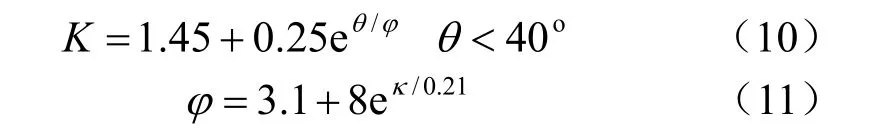
式中：K为荷载系数；φ为H/L影响系数。

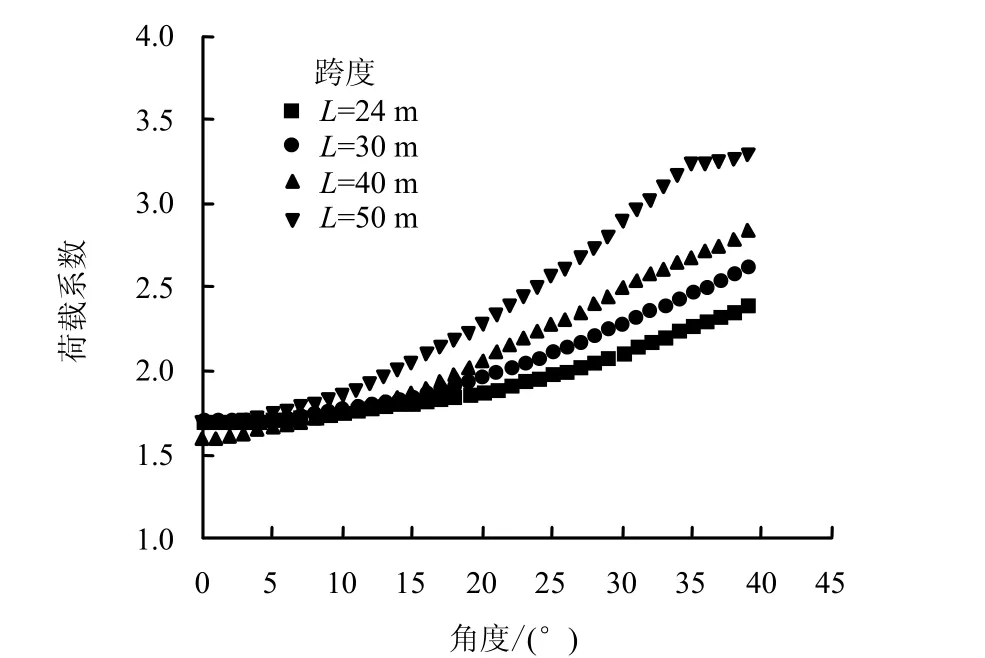
图11 不同跨度拱上荷载系数分布曲线（爆高7 m）Fig.11 Load factor curves of arches with different spans(with an explosion distance of 7 m)

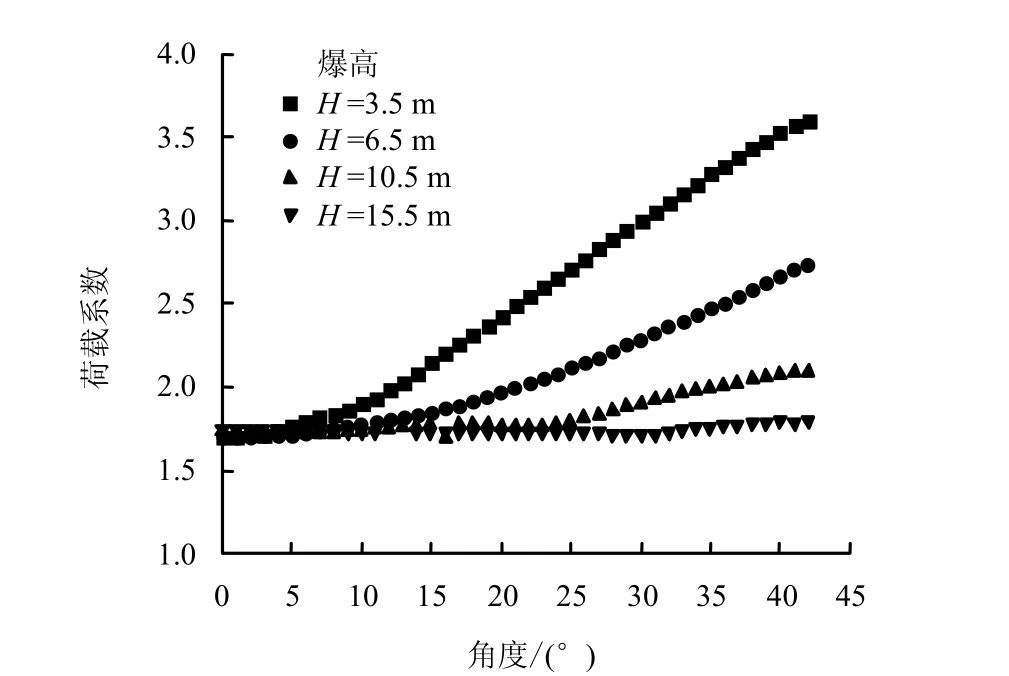
图12 不同爆高拱上荷载系数分布曲线（跨度30 m）Fig.12 Load factor curves at different explosion distances (with a span of 30 m)

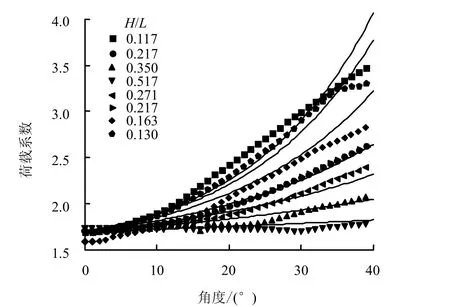
图13 拟合公式与数值计算结果对比Fig.13 Comparison between fitted equation and numerical calculation

图13对数值计算结果和式（10）的计算结果进行了对比，可以看出，当H/L较大时，即当爆高较大或跨度较小时，两者之间吻合得很好，当H/L非常小时，两者之间还存在一些误差；另一方面，当拱角较小时，两者的计算结果能够很好地吻合，而当拱角较大时，会出现小的误差。

5 算例分析

假定跨度为24 m，爆炸距离为6.5 m，TNT当量为324 kg时地下封闭爆炸，结合式（5）～（7）和式（10）计算得到拱形结构上荷载分布计算公式：

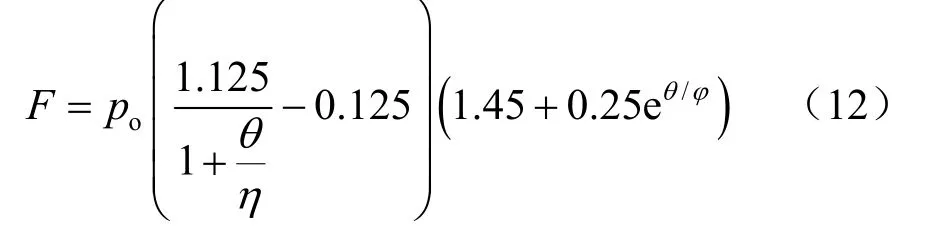
其中：

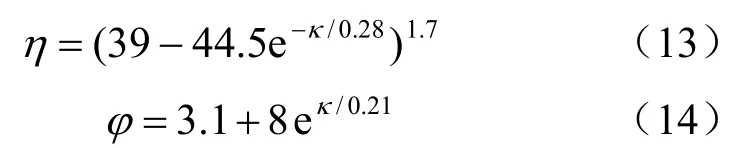
TM5-855-1提出[1]，可以采用固定的荷载系数K=1.5乘以自由场压力p得到拱结构上荷载。将式（12）计算结果与按照TM5-855-1给出的固定荷载系数方法及数值计算结果进行对比，如图14所示，可以看出，在拱顶时三者计算结果基本吻合，当偏离拱顶时，式（12）的计算结果与数值计算结果吻合，但与TM5-855-1方法计算结果产生了一定的差别，随着偏心角增加式，计算结果之间的偏差越大，说明，采用固定的荷载系数不能很好地描述爆炸应力波在地下拱形结构上的反射。

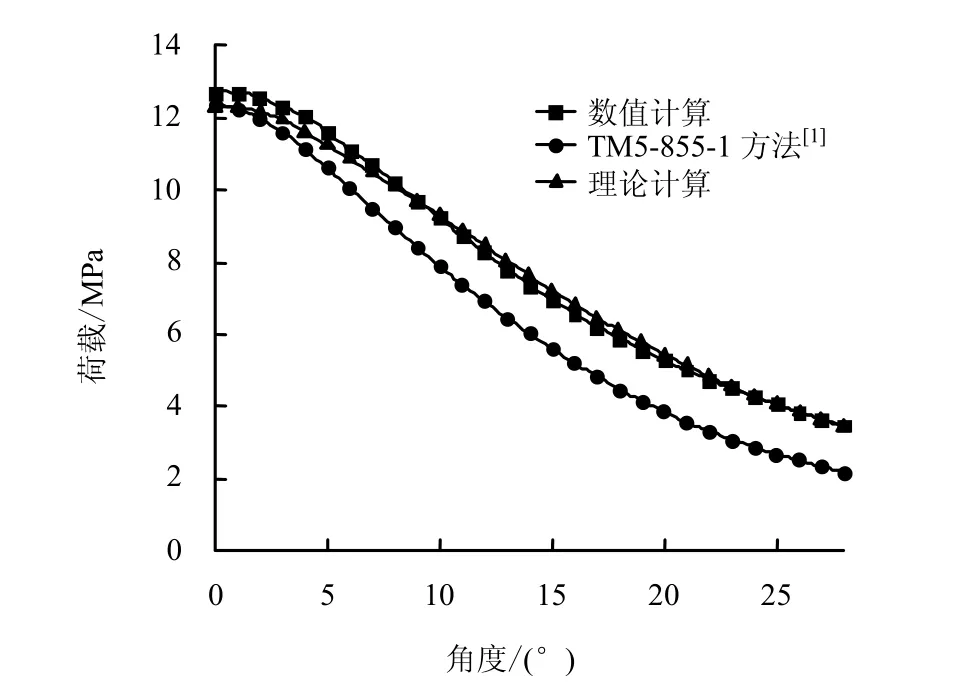
图14 拱形结构荷载分布曲线Fig.14 Distribution of blast loads on arch

6 结 论

（1）对于大跨度拱形结构，不同爆高、跨度会导致不同的荷载分布，但结构上，尤其是拱形结构上始终有荷载作用；而且不同时刻拱形结构上的荷载分布主要呈现以拱顶为对称轴的马鞍形分布形式。

（2）在跨度相同的条件下，随着爆高的减小，荷载的局部作用效应越明显；爆高越大，拱形结构上的荷载分布越均匀。在爆高相同的条件下，随着跨度的增加，荷载的局部作用效应越来越明显；当跨度减小，荷载的分布形式越趋于均布。

（3）研究表明，边墙荷载随着从墙顶开始沿着墙体逐渐衰减，最终趋于均匀。不同爆高及跨度情况下，沿着边墙的荷载分布曲线近似都可以分为两部分，边墙顶部至距顶部2.5 m处为荷载的衰减段，荷载近似呈线性衰减，从距离顶部2.5 m处向下，荷载近似均匀分布。在跨度相同的条件下，随着爆高的减小，作用于边墙的荷载随之减小，荷载分布越趋于均匀；在爆高相同的条件下，随着跨度的增加，荷载分布呈现相似的规律。

（4）给出了不同爆高、跨度情况下大跨度拱形结构荷载计算方法，并采用数值计算方法进行了验证。

（5）对应力波在拱上的荷载系数进行了分析，研究结果表明。在拱顶的荷载系数基本与TM5-855-1[1]吻合，荷载系数可以近似等于1.5，但沿着拱形荷载系数并不是固定值，在拱顶最小，随着拱角的增加而变大。计算结果也表明，当爆高与跨度之比越大，荷载系数在拱上的分布越均匀，即可以采用固定数值，当前研究结果表明，这一临界系数约等于1.5。

[1]TM5-855-1. Fundamentals of protective design for conventional weapons[S]. Vicksburg: US army engineers waterways experimental station, 1986.

[2]TM5-1300. Structures to resist the effects of accidental explosions[S]. Washington: Departments of the army, the navy and the air force, 1990.

[3]孙博. 爆炸作用下大跨度复合式结构荷载及其动力响应研究[D]. 南京: 解放军理工大学, 2007.

[4]范俊余, 方秦, 柳锦春. 炸药地面爆炸条件下土中浅埋结构上荷载的作用特点[J]. 解放军理工大学学报（自然科学版）, 2008, 9(6): 676－680.FAN Jun-yu, FANG Qin, LIU Jin-chun. Characteristics of loads on shallow-buried structures under the ground explosions[J]. Journal of PLA University of Science and Technology (Natural Science Edition), 2008, 9(6):676－680.

[5]DRAKE J L, FRANK R A, ROCHEFORD M A. A simplified method for the prediction of the ground shock loads on buried structures[C]//Proceedings of the First International Symposium on the Interaction of Non-nuclear Munitions with Structures. Florida: U.S. Air Force Academy, 1983: 191－121.

[6]WESTINE P S, FRIESENHAHN G J. Free-field ground shock pressure from buried detonations in saturated and unsaturated soils[C]//Proceedings of the First International Symposium on the Interaction of Non-nuclear Munitions with Structures. Florida: U.S. Air Force Academy, 1983: 216－227.

[7]钱七虎, 王明洋. 岩土中的冲击爆炸效应[M]. 北京:国防工业出版社, 2009.

[8]张宇, 范华林, 金丰年. 化爆作用下岩石介质自由场应力波拟合方法研究[J]. 岩土力学, 2011, 32(10): 3043－3047.ZHANG Yu, FAN Hua-lin, JIN Feng-nian. Weighted least squares fitting of free field equation of rock under chemical explosion[J]. Rock and Soil Mechanics, 2011,32(10): 3043－3047.

[9]王占江, 李孝兰, 戈琳, 等. 花岗岩中化爆的自由场应力波传播规律分析[J]. 岩石力学与工程学报, 2003,22(11): 1827－1831.WANG Zhan-jiang, LI Xiao-lan, GE Lin, et al. The free-field stress wave propagation of underground chemical explosion in granite[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(11): 1827－1831.

[10]Livermore Software Technology Corporation. LS-DYNA nonlinear dynamic analysis of structures[M]. California:Livemore, 1999.