关于抗震设计场地反应分析客观性的一些探讨

李 超，杨文武，张 旭，容肇鸿

（AECOM 亚洲，香港）

1 引 言

自20世纪70年代以来, 对于大型基础设施工程项目的抗震设计方法经历了巨大变革。基于强度和设计反应谱的传统设计方法，往往难以充分反映土壤场地效应对地震动的影响。而基于计算机方法的场地反应分析（如通用程序 SHAKE）可综合考虑输入地震波的时程数据以及场地土壤特性，所得结果具有较高的可靠度，在工程抗震设计中得到越来越广泛的应用。依照通用规范的传统设计方法则仅以地表峰值加速度PGA作为地震参数，对于场地特性的考虑也仅用单一参数（即土层类型）进行表示。相对而言，基于场地反应分析的设计方法可以考虑更多的输入信息，因而能够为抗震设计提供更为准确、可靠的依据。这一点对于模拟土层中的结构物（以下简称土层-结构系统），如挡土墙、桥墩、地下隧道等的地震反应分析尤为重要，因为在土壤-结构系统中，结构体与土层充分接触，系统的动力特性受其周边土层性质的显著影响。基于设计反应谱的单自由度弹簧-质量简化分析模型则难以充分反映这些复杂的影响因素。

在抗震设计实践中，由于场地反应分析其功能强大且简单易行，已经被工程界普遍采用，然而如未能正确建模和合理地选取动力参数，则极易产生较大偏差，甚至导致错误。本文通过敏感度分析对于场地反应分析结果的离散性进行研究，并且通过显式的方法直接考虑土层动力参数的不确定性以期对现行设计方法进行改进。此外，还特别研究软弱土层对于场地分析结果的影响。

关于敏感度分析，由于SHAKE程序对土层动力参数使用反复迭代的算法，土层输入参数的确定相当复杂，因此难以用经典统计学的方法进行量化分析。此外，普通工程设计人员受其教育背景和工程实践所限，往往对于统计学方法缺乏足够地认知和理解。针对以上具体操作困难，本文运用确定性分析方法，直接考虑各主要岩土动力参数的离散性及不同参数的相对重要性；在此基础上，对两个典型地质剖面综合考虑各参数不确定性的联合影响。上述方法均基于工程经验和理性考虑，可广泛地应用于一般工程的场地反应分析，作为一种系统的场地反应分析方法以改进现有工程实践。

2 模型设置

2.1 影响场地反应分析的主要因素

SHAKE程序的输入参数主要包括：现场土层分布、各土层的材料性质及边界条件。本文研究重点在于土动力参数的不确定性对于场地反应分析的影响。为此，考虑了两种典型地质条件，并确定了相应的几何参数、边界条件以及地震动输入波。输入地震波作用位置在基岩和土层的交界处。

用于地震动分析的土动力参数主要包括以下 3种：初始剪切模量G0（或最大剪切模量Gmax）、剪切模量衰减曲线和阻尼曲线。依场地而异，土层各动力参数均可具有相当程度的不确定性。首先，分别研究上述3种参数独立作用时，对地震动分析的影响。之后，考虑3种参数不确定性联合作用的影响。其他土层材料参数如密度、泊松比等由于可用较直接的方法得到，其不确定性可显著降低。因此，其他土层材料参数的不确定性对场地反应分析的影响在本文中将不作详细阐述。

2.2 典型地质剖面1：砂土场地

地质剖面1为砂土场地（见图1(a)），基岩深度为40 m，各土层为均质砂土。在SHAKE程序中，该场地以16层厚度为2.5 m的均质砂土土层模拟，其中各地层剪切模量随深度增加而增大。图1(b)显示了地质剖面1各土层初始剪切模量随深度的变化曲线。

2.3 典型地质剖面2：含软弱土层的砂土场地

地质剖面2中各土层设置与剖面1基本一致；不同之处在于剖面2场地中包含一层厚为5 m的软弱土层（见图2(a)）。在实际工程中，各场地软弱土层的埋藏深度不尽相同；为此，本文特地分析了软弱层的埋藏位置对场地分析的影响。图2(b)给出了对于地质剖面2当软弱土层的位置在15～20 m深度时，各土层初始（或最大）剪切模量随深度的分布。

图1 典型剖面1土层分布及初始剪切模量曲线Fig.1 Strata and initial shear modulus curve of typical geological profile 1

图2 典型剖面2土层分布及初始剪切模量曲线Fig.2 Strata and initial shear modulus curve of typical geological profile 2

表1给出了地质剖面1、2各土层主要参数取值。对于砂土，初始（或最大）剪切模量按照Seed等[1]于1984年提出的方法，根据标准贯入试验N值计算得出。对于软土层，初始模量由假定的剪切波速Vs=100 m/s计算得出。

2.4 土的动力参数

2.4.1 初始（或最大）剪切模量

初始（或最大）剪切模量可由试验直接测量，或通过与原位测试（如标准贯入试验及静力触探试验）的经验关系获得。文中采用了基于标贯试验的方法。图3显示了作者参与的一个项目中标贯击数N值的分布情况（由 AECOM 公司提供）。由图 3可知，在该项目中N值上、下限偏离平均值约50%。

表1 地质剖面1、2各土层参数Table 1 Parameters of soil layers for typical profiles 1 and 2

图3 典型标准贯入试验SPT-N值随深度之变化Fig.3 Typical SPT-N values vs. depth

2.4.2 土的动力曲线

土的动力曲线包括剪切模量衰减和阻尼曲线。本文采取了美国电力研究学会EPRI[2]在1993年建议的一套土的动力曲线作为标准，该曲线反映了上覆土层的影响（见图4、5）。图4中G为剪切模量。在很多大型基建工程中，土的动力曲线由室内动态三轴试验得出。但关于试验结果的详细分析、对于试验的局限性以及各项误差和不确定性的分析常常不够完善。作为其可能后果之一，设计工程师往往对于数据的可靠性和离散性缺乏充分地认识。

图4 EPRI砂土剪切模量衰减曲线 (0～75 m)[2]Fig.4 EPRI shear modulus degradation curves for sandy soils at depth 0-75 m[2]

图5 EPRI砂土阻尼曲线 (0～75 m)[2]Fig.5 EPRI damping curves for sandy soils at depth 0-75 m[2]

因此，笔者建议，为更好地应用试验数据以及降低出错概率，设计工程师可将试验得出的动力曲线和国际通用的曲线进行比较，并借此来帮助判断曲线的有效性。在这里笔者并非主张国际通用的动力参数曲线（如EPRI[2]）可以直接替代适合具体工程项目的试验曲线。这里所强调的是通过将实验室实测数据与国际通用动力参数曲线的对比，减少由于采用不适当的试验曲线而带来的设计风险。

为了说明土的动力曲线的不确定性，在图6、7给出了 EPRI[2]层深 0～6 m 砂土的动力曲线。在EPRI[2]的研究报告中，该曲线通过50条随机剪切模量的衰减曲线和阻尼曲线的中间值得出。由图可见，这些动力曲线之间存在着相当大的差异。为了量化其离散性，选择了剪切应变γ=0.1%作为一个比较尺度；在该应变水平下，比较各曲线对应该应变之剪切模量和阻尼比的上、下限值和中间值（注：在普通地震分析中，应变水平通常在 0.01%到 1%之间）。我们注意到：该组曲线中，剪切模量的衰减曲线之上、下限偏离中间值为55%，而阻尼曲线偏离约为40%。

在具体工程项目中，由于经费和条件的限制，所进行的动力试验以及从中得到的土的动力曲线的数目往往不够充足。甚至在一些造价上百亿人民币的大型工程项目中，对于某些土层都只有1、2条实测曲线。相比较而言，EPRI[2]曲线由大量数据综合得出，因而具有重要的参考价值。应该清醒地认识到，如果在实际工程项目的动力曲线仅仅由 1、2个动力试验得出，那么即使试验得出的曲线具有良好的收敛性，其结果的可靠性亦值得商榷。事实上由 EPRI曲线的显著离散性可见，真实的动态曲线的数据分布范围可能会远超过个别试验结果。本文之后的章节也会进一步阐述由于土的动力曲线的离散性可能导致的地表峰值加速度 PGA预测值的显著差异。

图6 EPRI (0～6 m)砂土剪切模量衰减曲线及其离散性[2]Fig.6 EPRI randomized shear modulus degradation curves for sandy soils at depth 0-6 m[2]

图7 EPRI (0～6 m)砂土阻尼曲线及其离散性[2]Fig.7 EPRI randomized damping curves for sandy soils at depth 0-6 m[2]

3 典型剖面1敏感度分析

3.1 综述

如上所述，标准贯入试验数据和土的动力曲线等岩土动力分析参数及土的动力测试获得的数据通常具有较大离散性。当使用从实验室或现场试验选取设计参数时，需要对不确定因素加以适当考虑并给出合理的估值范围。对于地震动场地反应分析，这些结果通常表现为对地表峰值加速度 PGA的合理估计。在现行的常规设计中，通常在设计初期考虑这些不确定因素，再根据各种限制条件选取一条平均曲线来进行设计。但这种选择方法并未考虑不确定因素随分析步骤的传递性；换言之，关于不确定性的考虑及其离散范围未能在其后的分析步骤中得到反映。其后果直接导致在建筑物的基础或结构等后期设计中无法适当反映这些不确定性因素的影响。故从本质而言，这种方法未能合理考虑不确定因素对最终设计的综合影响。

由于工业界设计工程师未必熟悉统计方法，本文面临的挑战之一是如何运用工程师熟悉的、非统计学的方法来处理这些不确定性，以确保该方法可易于推广使用。在此建议如下：首先针对每个主要影响因素进行敏感度分析，得到各因素独立作用时其不确定性对最终结果PGA的影响；然后再综合考虑多种因素的共同作用，得出各参数不确定性对于PGA的综合影响，并确定下一步抗震设计所需要的上、下限PGA值。

在这些敏感度分析中，选用了日本道路协会《公路桥梁设计规范第5部分：地震设计》[3]所提供的一个典型地震时程曲线（简称为日本3号地震波）作为输入地震波；并对该地震波进行了线性缩放，令缩放后的基岩PGA的数值达到0.15g。图8给出了该地震波的时程曲线。

图8 输入时程曲线: 日本3号地震波Fig.8 Time-history of input motion: Japanese No.3 motion

3.2 典型剖面1：单一不确定因素的影响

以SHAKE为工具进行场地反应分析时，其主要输入参数包括初始（或最大）剪切模量和土的动力曲线。为了进行敏感度分析，首先，运用各参数的平均曲线或最优估值进行一次场地反应分析，并将其分析结果选取为标准值（若分析结果为PGA，这一标准值以来表示）；其次，考虑由单一因素的离散性对于场地反应分析的影响。为简便起见，当某一土层动力参数偏离平均曲线时，假设所有16层土的动力曲线依相同模式变化。即若某一因素以一定比例偏离从平均（最佳估计）值变化，假设所有16层土壤均发生相同程度的偏离。通过这种简化方式，可使所需敏感性分析数量大为减少。值得注意的是，实际工程中应充分考虑不同土层参数发生不同程度、不同方向偏离的可能性。

图9(a)、9(b)、9(c)分别为初始剪切模量、阻尼曲线和剪切模量衰减曲线对 PGA的敏感性分析结果。图 10(a)、10(b)、10(c)分别显示了为初始剪切模量、阻尼比曲线和剪切模量衰减曲线相对于敏感性分析标准值发生偏离时对于最终结果 PGA发生影响的关系曲线。由以上各图可知，PGA与初始模量及剪切模量衰减曲线的关系均呈高度非线性，只有PGA与阻尼比曲线的对照关系接近于线性。

图9 典型剖面1各土层最大加速度随深度分布Fig.9 Maximum accelerations vs. depth for typical profile 1

图10 典型剖面1敏感性分析曲线Fig.10 Sensitivity curves for typical profile 1

3.3 典型剖面1：考虑多种不确定因素的联合影响

针对上述3种不确定性因素联合作用时对场地反应分析成果PGA的影响进行了研究。由2.4节得到，G0的离散性约为50%，剪切模量衰减曲线约为55%，阻尼曲线约为40%。首先由场地土平均动力曲线及G0最佳估计剖面进行场地反应分析，以确立PGA比较中的标准值。图11显示了对3种不确定因素综合影响的工况分析树状图。对所有动力曲线和初始剪切模量曲线的可能组合，分析了该组合工况下预测PGA相对于平均值的偏离量。可以明显地观察到，由于3种不确定性因素的联合作用，最终由场地分析得出的 PGA值相对于平均值的偏差，下侧约为-39%而上侧约为23%。图12给出了产生上、下限值的各因素不确定性偏差的组合。图13显示了由平均剪切模量和动力曲线对PGA产生的综合影响，得到其对的偏差的等值线图。由于本研究只针对一个典型地质条件设置，其具体结果的数值未必具有普遍性。然而上述研究所揭示的关于PGA结果的离散性则具有广泛的适用性。

由于场地反应分析各因素的不确定性，造成了最终结果的普遍离散性。相应而言，对于大型基础设施项目的工程设计，关于PGA值的选取应该特别谨慎。一般而言，由场地分析得出的PGA估计不宜采用单一的数值，而应该考虑数据的离散性。我们可以考虑PGA的上、下限或者标准差以反映其内在的不确定性。对这种不确定性的评估将进而对建筑物或挡土墙的抗震分析和抗震设计产生显著影响。对于地震分析的许多其他方面，如液化分析或土与结构相互作用的分析，这种不确定性对于最终计算成果及工程设计亦可产生重大影响。

图11 初始模量、阻尼比曲线及剪切模量衰减曲线各不确定因素综合作用联合影响树状图Fig.11 Combined effects of uncertainty due to initial moduli, damping ratio and shear modulus degradation curves

图12 PGA预测值上、下限所对应的不确定因素影响组合Fig.12 Combinations of uncertainties corresponding to maximum deviation from mean PGA

图13 阻尼和剪切模量衰减曲线对PGA的联合影响Fig.13 Effects on PGA due to combination of damping and shear modulus degradation curves (constant G0)

4 典型剖面2敏感性分析

在工程实践中，具有软弱土层的工程场地越来越常见。本节将探讨由于软弱土层的存在对场地反应分析产生的特殊影响。首先假定软弱土层的深度在15～20 m，重复地质剖面1的敏感性研究。其次，将考虑软弱土层层深位置变化及其对于地震场地反应分析的影响。

4.1 初始模量、阻尼曲线和剪切模量曲线的影响

针对典型地质剖面 2，各动力参数的不确定性对场地反应分析成果 PGA的影响进行分析（见图14、15）。图14(a)、15(a)给出了由于初始剪切模量G0的不确定性对PGA的变化曲线。图14(b)、15(b)为阻尼比曲线与PGA的变化关系。图14(c)、15(c)为剪切模量衰减曲线对PGA的变化关系。值得注意的是，类似于3.2节，仍然是阻尼曲线对PGA的变化曲线接近线性，但阻尼曲线的影响变弱，其主要原因为是由于软弱层对于地震动的强烈阻尼作用。初始模量和剪切模量的衰减曲线对 PGA的变化曲线仍然为非线性。为简单起见，本文不再重复各种不确定因素对PGA预测的联合影响。

图14 典型剖面2各土层最大加速度随深度分布Fig.14 Maximum accelerations vs. depth for typical profile 2

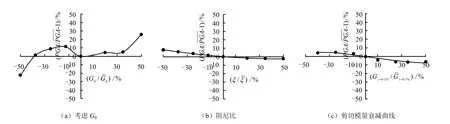
图15 典型剖面2敏感性分析Fig.15 Sensitivity curves for typical profile 2

4.2 软弱土层位置的影响

假设软弱层层厚为5 m，其埋藏位置在0～40 m间以5 m为间隔随机分布。图16显示了假定软弱层在不同位置时各土层最大加速度分布包括地表峰值加速度PGA的取值。由图可知，软弱层的位置变化对PGA预测值有显著影响。在无软弱层存在时，地表峰值加速度 PGA即是全场地各土层的最大加速度Amax_site。而在软弱土层存在的情况之下，PGA往往不等于 Amax_site；而全场地最大加速度 Amax_site通常发生于软弱土层之下。

图16 软弱土层埋深与各土层最大加速度之敏感性分析Fig.16 Maximum accelerations for sensitivity study with regard to location of weak layer

这一发现可对场地土层液化评估及其他基于PGA的抗震设计工作产生重要的影响。因为通常给予有效循环剪切应力分析的液化判别主要基于两个主要参数：PGA和地震震级。Youd等[4]指出，在地震场地反应分析中，土层最大加速度随着深度的增加而减小。由图 16可知，软弱土层存在与否，对PGA预测有显著影响。所以，当软弱土层存在时，现有液化分析判别方式（如Youd等[4]）未经有效修正时，可能无法准确地估计砂质场地土的液化潜能。图17显示了软弱土层对PGA和场地土最大加速度Amax_site的影响。可以看到，由于软弱层的存在，PGA与全场地最大场地加速度Amax_site不复相同，从而难以采用 PGA一个单一数据来代表整个场地土层的特性。而与此相应的许多抗震设计准则包括土的液化判别准则也应该给予充分考虑或做出相应的修正。

图17 软弱土层埋深对PGA以及全场地最大加速度Amax_site的影响Fig.17 Effects of weak layer location on PGA and Amax_site

5 结 论

本文研究了以SHAKE为工具进行场地土场地反应分析的通用方法，分析了场地反应分析各因素的不确定性，并提出了一种理性的方法以系统性地考虑各个岩土参数的不确定性。该方法的要点可以总结如下：

（1）确定场地反应分析的基本输入参数（包括基岩输入地震波、土壤分层等）。

（2）对各种主要参数确定其离散性，给其数值变动的上、下限（上下限初步可定为偏离平均值一个标准差）。这些参数包括于：①土壤动剪切模量，②土壤动力阻尼曲线，③土壤剪切模量衰减曲线。

（3）在场地反应分析中，运行一套以平均值（或最优估计值）为基础的场地反应分析，并作为比较的标准值。

（4）通过变动一个或多个SHAKE输入参数、重复进行多套场地反应分析。

（5）提供分析结果（如地表PGA）时，同时提供其上、下限，如有可能可进一步提供其标准差，为抗震设计提供充分的信息。

本文运用这种简化的系统性分析方法，通过敏感性分析，以保证抗震设计本身内在的不确定性得到充分考虑。本文还针对包含软弱土层的场地进行了专门研究，揭示了软弱土层对于PGA预测值的显著影响。

因篇幅所限，本文未考虑输入地震波的不确定性以及等效线性的场地反应分析法在处理强烈非线性问题时可能产生较大误差的问题。对于强烈非线性问题，Borja等[5]提出了一种系统考虑土壤非线性的本构关系模型；在计算方法实现的层面，Li等[6]给出了一种严谨的考虑土-水耦合作用及大变形动力问题的有限元方法。对于强震作用下的场地反映分析（如基岩加速度大于0.2g），本文所代表的简化方法有明显的局限性；Borja等[5]、Li等[6]所代表的理论性较复杂却更严谨的计算方法应该得到应用。此外基于统计学的方法也可以结合本文适当运用以进一步量化风险。

本文的研究成果可以用于一系列的工程应用，包括土层液化分析、土层-结构相互作用分析、结构动力分析。并可以对工业及民用建筑、挡土墙、桥梁基础、隧道等土层-结构系统的抗震设计和分析提供借鉴。

[1]SEED H B, WONG R T, IDRISS I M, et al. Moduli and damping factors for dynamic analyses of cohesionless soils[J]. Journal of Geotechnical Engineering, ASCE,1984, 112(11): 1016－1032.

[2]Electric Power Research Institute. TR-102293 Guidelines for determining design basis ground motions[S]. USA:Electric Power Research Institute, 1993.

[3]日本道路协会. 公路桥梁设计规范第 5部分: 地震设计[S]. 日本: 日本道路协会, 2002.

[4]YOUD T L, IDRISS I M, ANDRUS R D, et al.Liquefaction resistance of soils: Summary report from the 1996 NCEER and 1998 NCEER/NSF workshops on evaluation of liquefaction resistance of soils[J]. Journal of Geotechnical and Geoenvironmental Engineering,2001, 127(10): 817－833.

[5]BORJA R I, AMIES A P. Multiaxial cyclic plasticity model for clays[J]. Journal of Geotechnical Engineering, ASCE, 1994, 120(6): 1051－1070.

[6]LI C, BORJA R I, REGUEIRO R A. Dynamics of porous media at finite strain[J]. Computer Methods in Applied Mechanics and Engineering, 2004, 193(36－38): 3837－3870.