球面波加载下黄土线黏弹性本构关系

卢 强，王占江，李 进，郭志昀，门朝举

（西北核技术研究所，西安 710024）

1 引 言

黄土主要分布在干旱与半干旱地区，对其力学性质的清晰认识在防震减灾问题、环境工程问题及地下爆炸研究中具有非常重要的作用。对于土类介质本构模型的研究引起了众多研究者的兴趣。崔伟华等[1]通过位移反分析方法，结合遗传算法对黄土的非线性本构模型参数进行了反演分析。马君伟等[2]利用等应变直剪仪对马兰黄土原状土进行了剪切松弛试验，采用三参量黏弹性固体模型对试验数据进行了分析，确定了马兰黄土的黏滞系数。上述文献是基于静态试验方法对黄土的非线性力学性质进行的研究。Song等[3－6]则以改进的SHPB试验方法对软介质（砂、土等）进行了动态试验，对孔隙率、含水率等对介质动力学特性的影响做了讨论，为软介质动力学特性的研究提供了可借鉴的研究思路。

对于地下爆炸研究而言，利用微型炸药球实现球面发散波加载的试验技术是模拟地下爆炸中介质的应力-应变状态最为接近的技术手段[7]。从20世纪50年代以来，国外发展了球形空腔爆炸理论[8－9]，研制了用于模拟地下爆炸加载的微型炸药球并发展了粒子速度、应力测试技术，结合试验数据（粒子速度和应力测量波形）和拉格朗日分析方法[7,10]或其他研究方法深入研究了核爆炸现场岩体和土体的动态本构关系。

从国内公开发表的文献看，在试验方面，王占江等[11－12]研制了不同规格的泰安微型炸药球（0.125～27 gTNT当量，直径φ=5～30 mm），利用此类精密爆炸源，结合圆环型粒子速度测试技术得到了部分典型地质介质（如黄土、花岗岩等）中关于球形填实或空腔爆炸的重要试验结果，这对国内球面波试验技术的发展奠定了基础。在理论方面，李孝兰[13－14]在对国外文献总结的基础上，对弹性固体介质中的球形空腔爆炸理论进行了较为详尽地分析，所得结果对于指导试验研究具有重要作用。林英睿等[15－16]则以花岗岩中实测球面波粒子速度波形为基础，采用拉格朗日分析方法对花岗岩的本构进行了研究，得到了一些初步结论。但由于在目前的球面波试验中很难同时完成粒子速度及径向或切向应力的测试，这对于拉格朗日反分析方法的完备性来说是不利的，在通常的处理中一般是要加入一定的本构假定去完备求解方程。

近来，赖华伟等[17－18]基于球面波试验得到的径向粒子速度数据，以线黏弹性 ZWT方程假定为基础，采用特征线方法对有机玻璃中的 ZWT参数反演做了深入的研究，所得参数对有机玻璃的黏弹性力学行为有较好的描述。卢强等[19]则以线黏弹性ZWT本构方程为基础，对球面波动力学方程进行了理论推导，得到了以位移u描述的三阶波动方程，以谐波解的形式详细讨论了线黏弹性球面波的吸收和弥散效应，这对于认识黏弹性球面波的传播演化规律具有一定的实际意义。

本文将以黄土中球面发散波试验数据为依据，结合基于线黏弹性 ZWT方程得到的黏弹性球面波的传播规律，对黄土的黏弹性本构特征进行研究。

2 黄土中的球面发散波试验

国内利用柔爆索中心起爆微型炸药球激发球面发散波技术及圆环型粒子速度测试技术已发展地较为成熟，并成功应用在诸多研究领域。黄土中球面发散波试验采用的试验装置及测试技术与文献[20]是一致的。这种试验装置可通过在黄土样品上钻孔、回填等工序，置换不同的中心爆室模型以达到样品重复利用的效果。中心爆室模型可根据模拟源区介质或爆室结构的不同进行加工，爆室介质或结构（如带有空腔、环槽等结构）不同，通过预埋的圆环型粒子速度计测量到粒子速度波形也不相同，由此可开展爆炸源区介质或近区结构对爆炸应力波影响的相关研究[20]以及介质动力学本构特性研究。

3 利用粒子速度数据对黄土基本力学量预估

采用 0.125 gTNT当量的微型炸药球作为爆炸源，其所产生的塑性区半径不超过60 mm，而黄土球面波试验装置中预埋的粒子速度计的最小半径为90 mm，所以本文测得的粒子速度均是介质弹性响应的结果[20]。图 1给出了球面波加载下 180～1 280 m·kt-1/3范围内的19个粒子速度曲线。

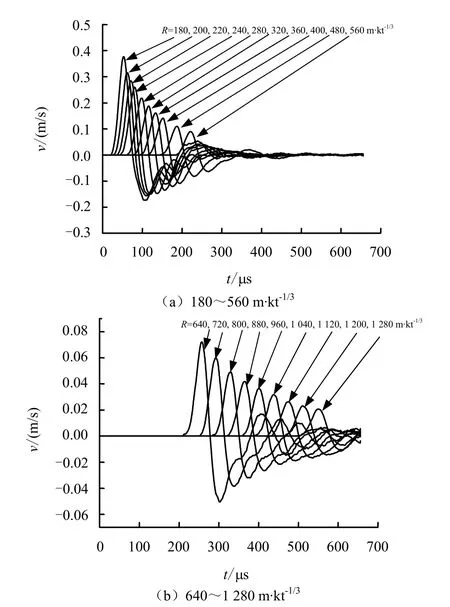
图1 粒子速度曲线Fig.1 Curves of particle velocity

从图1可以看出，0.125 gTNT当量的微型炸药球在黄土中激发的球面波持续时间约400～500 µs，上升沿约 30～40 µs，它们均比花岗岩中的持续时间（约10 µs量级）、上升沿（约µs量级）要大很多[11－12]，这体现了软岩和硬岩中球面波传播特性的差异。由于球面波加载下介质承受的应变状态为三维应变状态，随着传播距离的增加，其应变状态越来越接近一维应变状态[21]，即径向应变εr将主导介质的变形特征，切向应变εθ的贡献较小。因此，近似认为，粒子速度幅值对应时刻黄土中传播的球面波的径向应力和径向应变满足下面两个强间断波的相容条件：

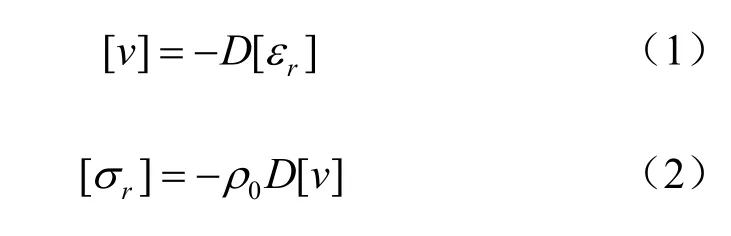
通过式（1）、（2），由粒子速度幅值vmax、波速D及密度ρ0能够求出粒子幅度最大值时刻的径向应变εr、径向应力σr。对于球面波，还存在粒子幅度最大值时刻对应的切向应变εθ、切向应力σθ需要确定。切向应变εθ的确定可通过式（3）确定，

式中：u为径向粒子位移；r为物质坐标。切向应力σθ的确定存在一定的困难，此处作类似弹性本构方程的定义，εr、εθ、σr、σθ之间的关系可表示为

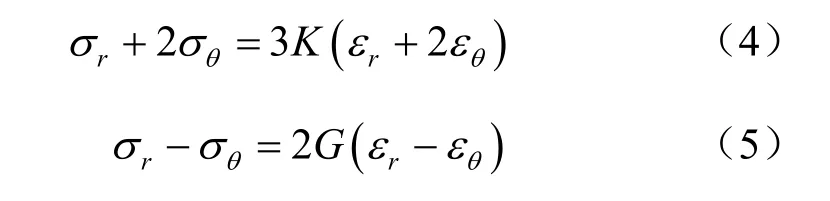
表1中的负号代表压缩状态。由表1可以看出，径向应变εr和切向应变εθ分别处于压缩和拉伸状态，其变形量随比距离的增大而减少，但越来越大，这说明随着传播距离的增加，径向应变εr将主导介质的变形，这一点和球面波加载下介质应变状态趋于一维应变状态的理论结果是一致的。另外，结合粒子速度数据，由式（4）、（5）反演得到了弹性模量 E=(1.927±0.216)GPa、体积模量 K=(1.284±0.144)GPa、剪切模量 G =(0.771±0.086)GPa，上述数据可作为 ZWT本构参数反演所用到的基本力学量。

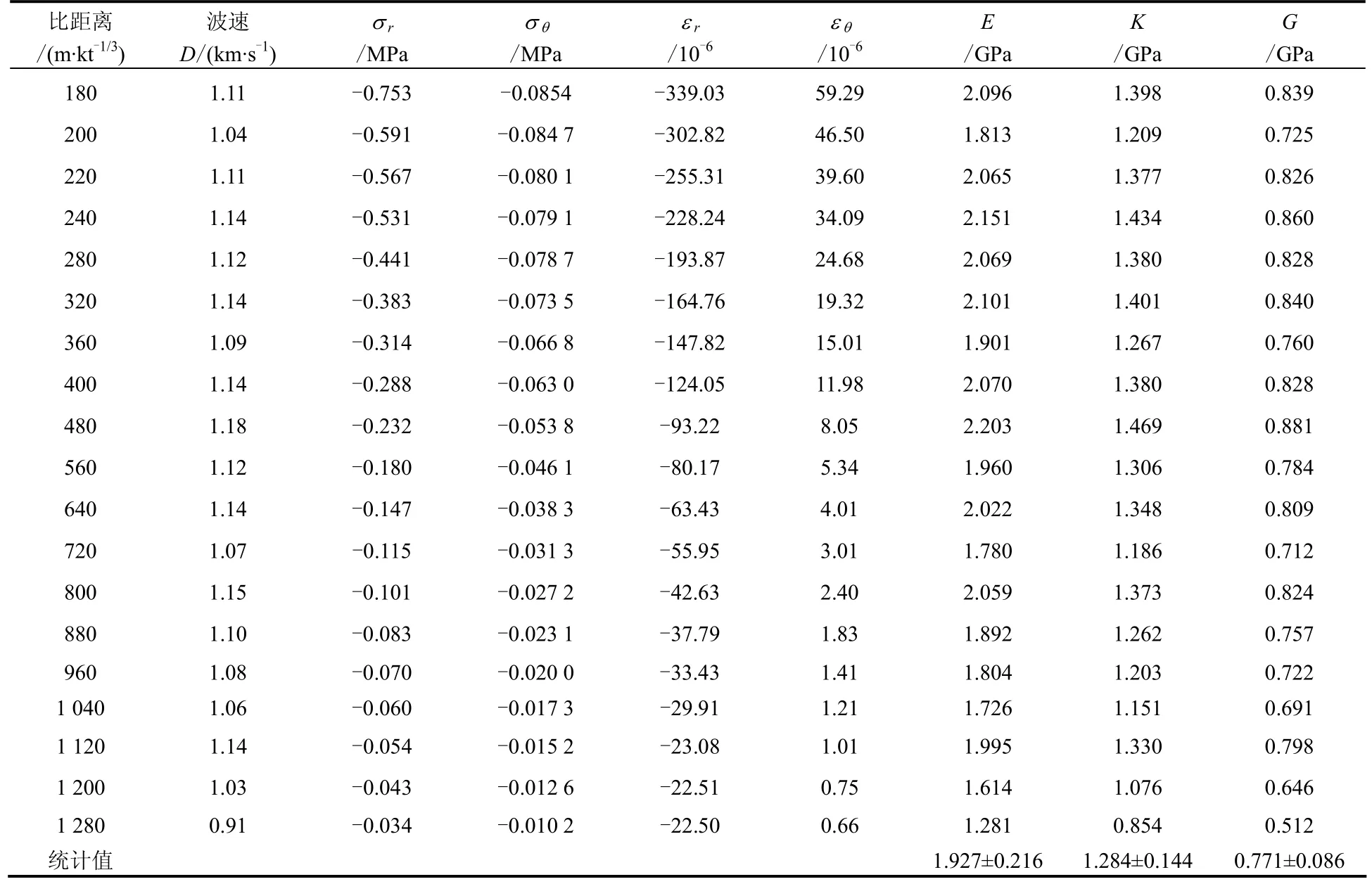
表1 由粒子速度数据反推的黄土基本力学参数Table 1 Basic mechanical parameters of loess calculated from the particle velocity data

4 基于球面波试验数据的线黏弹性ZWT本构参数反演

由文献[17－18]的讨论可知，对于1～102µs时间尺度的爆炸冲击载荷作用，ZWT本构关系可忽略低频Maxwell体的松弛效应，其本构可表示为一个线性弹簧并联一个高频的Maxwell体，如图2所示。在球坐标下，线黏弹性 ZWT本构方程容变律及畸变律的率形式可以写为

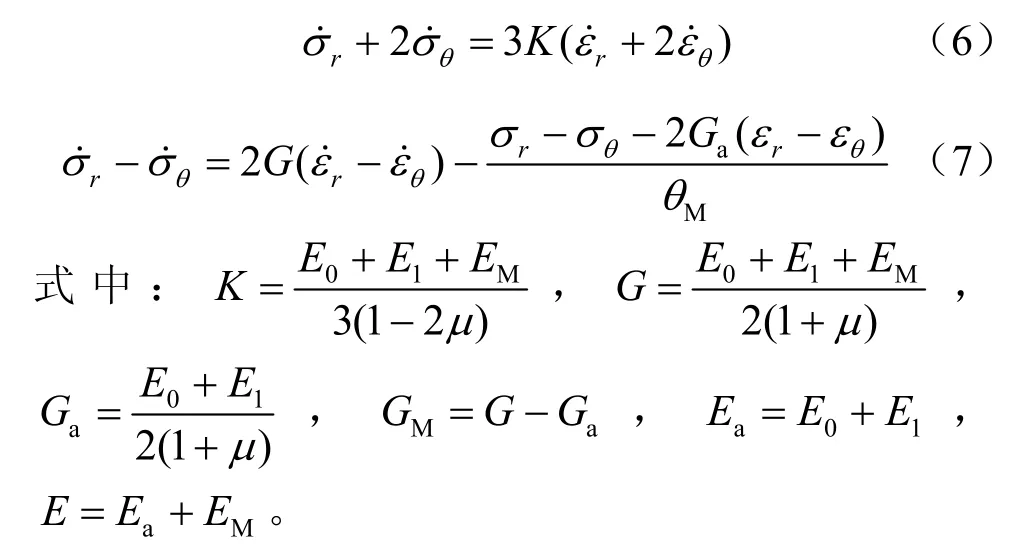
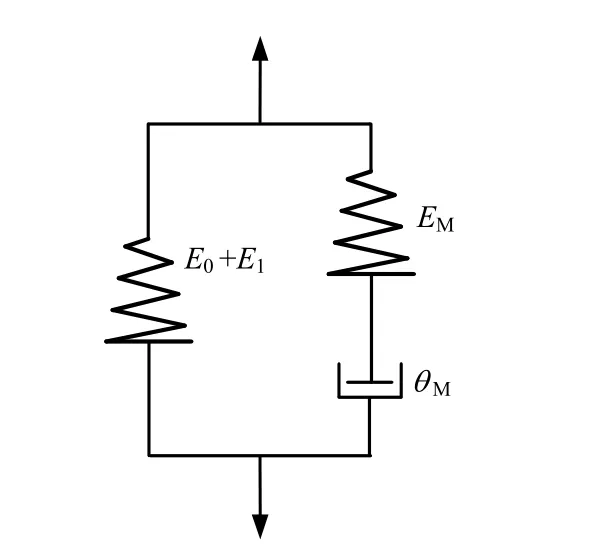
图2 线性黏弹性ZWT本构模型Fig.2 Linear viscoelastic ZWT constitutive model

基于线黏弹性ZWT本构方程，赖华伟等[17－18]采用特征线法推导出的强间断球面波衰减因子α和卢强等[19]对谐波解的分析给出的高频球面波的衰减因子α是一致的，衰减因子可表示为

在文献[17－18]中，赖华伟等基于强间断假设，结合球面波加载下有机玻璃中的径向粒子速度幅值及波速数据拟合出了式（8）中的高频波衰减因子α，再利用有机玻璃的准静态参数Ga，给出了线黏弹性ZWT本构方程中的GM、θM参数，从而完成了对有机玻璃黏弹性参数的反演。在此需指出的是，文献[17－18]并没有考虑介质的非线性黏弹性特性。对于黄土中的球面波结果，由表1可知，径向应变εr、切向应变εθ均远小于0.01，可以忽略黄土的非线性项的影响[21]。前面已经提到，粒子速度的上升沿达到了30～40 µs，若对其中传播的球面波采用强间断假设则显得较为牵强，由此拟合得到的衰减因子α的误差相对较大。由式（6）、（7）可知，对于线黏弹性ZWT本构方程，只需确定K、G、GM（或Ga）、θM4个参数即可。K和G可采用表1给出的预估参数，但GM（或Ga）和θM目前尚不能确定。即使进行准静态试验确定了GM（或Ga），但由粒子速度幅值数据拟合式（8）中的高频波衰减因子的前提（高频波或强间断波）会受到质疑。可见采用黄土中的球面波数据对其黏弹性本构进行反演需考虑新的思路。

由前所述，在黄土球面波试验中，预埋的 19个粒子速度计分布在φ180～1 280 mm范围内，最小量计的半径为90 mm。这里假定不考虑炸药球与源区介质的相互作用过程，仅取半径90 mm处粒子速度计测量得到的粒子速度波形作为边界条件，以线黏弹性ZWT本构作为黄土介质的本构描述（K和G采用表1给出的参数，Ga和θM按一定方式组合），采用一维球面波差分计算程序计算波在黄土中的传播，以输出的粒子速度幅值、位移幅值及其对应的时间数据和试验结果通过式（9）定义的误差函数进行对比来确定Ga和θM。误差函数Error(Ga，θM)为

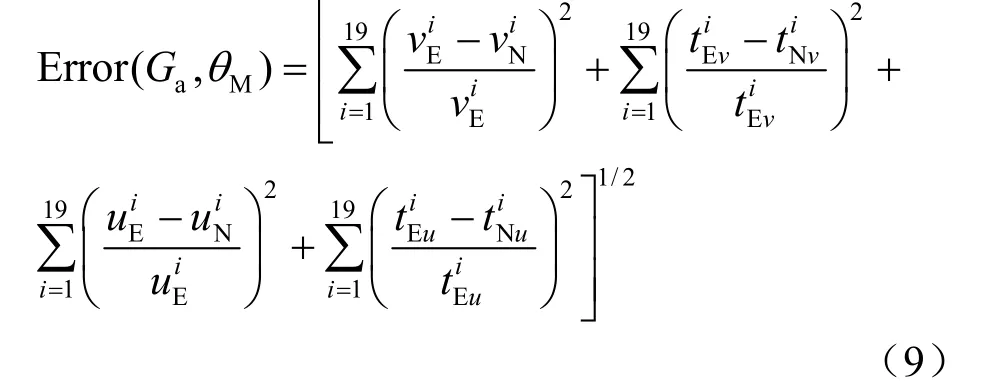
考虑到Ga＜G，计算中Ga取值区间定为0.50～0.70 GPa，间隔为0.01 GPa，θM取值区间为10～60 µs（参考波的上升沿大小），间隔为1 µs。图3给出了式（9）所表征的误差函数的等值线图。等值线的疏密变化实际上表征了误差函数 Error(Ga,θM)随参数Ga和θM的变化快慢。等值线密集的区域，误差函数对参数Ga和θM的数值变化较为敏感，等值线疏松的区域，误差函数对参数Ga和θM的数值变化敏感度较小。图3中的黑色圆点代表由式（9）计算的最小误差，其值为0.233，对应Ga=0.64 GPa（GM=0.13 GPa）、θM=21 µs。采用此参数对黄土中的球面波传播过程进行数值模拟，图4～8给出了数值模拟结果和试验结果的对比图。图4和图5分别是粒子速度和粒子位移幅值随比距离的变化曲线，可以看出，数值模拟结果与试验结果的吻合程度比较令人满意，粒子速度幅值的偏差在±8%以内，位移幅值的偏差在±6%以内。图6和图7分别是粒子速度幅值对应时刻和粒子位移幅值对应时刻随比距离变化曲线，粒子速度幅值时刻的偏差在±1%以内，位移幅值的偏差在±5%以内。图8给出了数值模拟得到的粒子速度曲线和试验曲线的对比图，其中实线代表试验结果，带有不同形状符号的线是数值模拟结果。可以看出，模拟得到的粒子速度曲线与试验曲线具有较好的一致性，这说明利用上述方法反演出的本构参数基本反映了黄土介质的黏弹性动力学特性。

作为进一步的说明，图9给出了粒子速度幅值对应时刻的径向应力σr、切向应力σθ随比距离R的变化。图10给出了粒子速度幅值对应时刻的径向应变εr、切向应变εθ随比距离R的变化。图9、10中同时加绘了表1中给出的相关数据，从图中可以看出，采用式（1）～（5）给出的σr、σθ、εr、εθ和由数值模拟得到的相应结果之间具有比较令人满意的一致性，这说明表1给出的黄土基本力学参数弹性模量E、体积模量K及剪切模量G与基于ZWT本构反演的黏弹性本构参数之间具有自洽性，同时也证明了用球面波加载下的粒子速度数据，结合上述处理方法去研究黄土介质粘弹性本构的可行性。

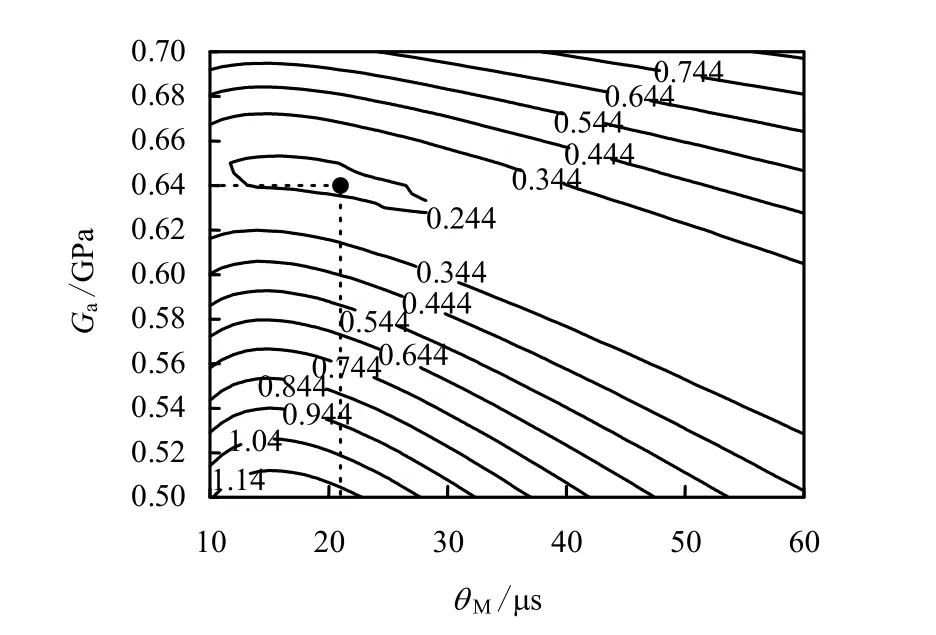
图3 误差函数的等值线图Fig.3 Isoline diagram of error function

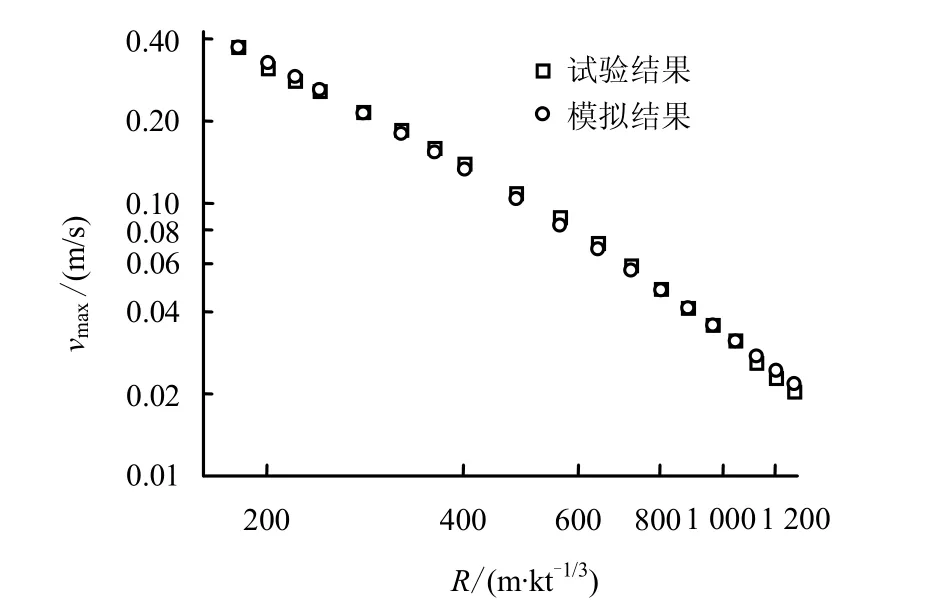
图4 粒子速度幅值vmax随比距离R的变化情况Fig.4 Variations of vmax with R

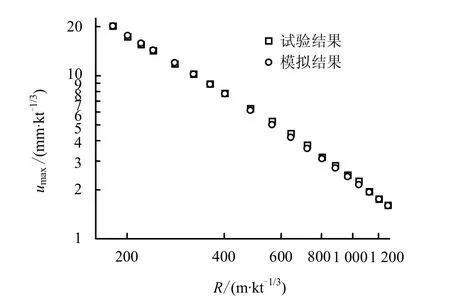
图5 粒子位移幅值umax随比距离R的变化情况Fig.5 Variations of umax with R

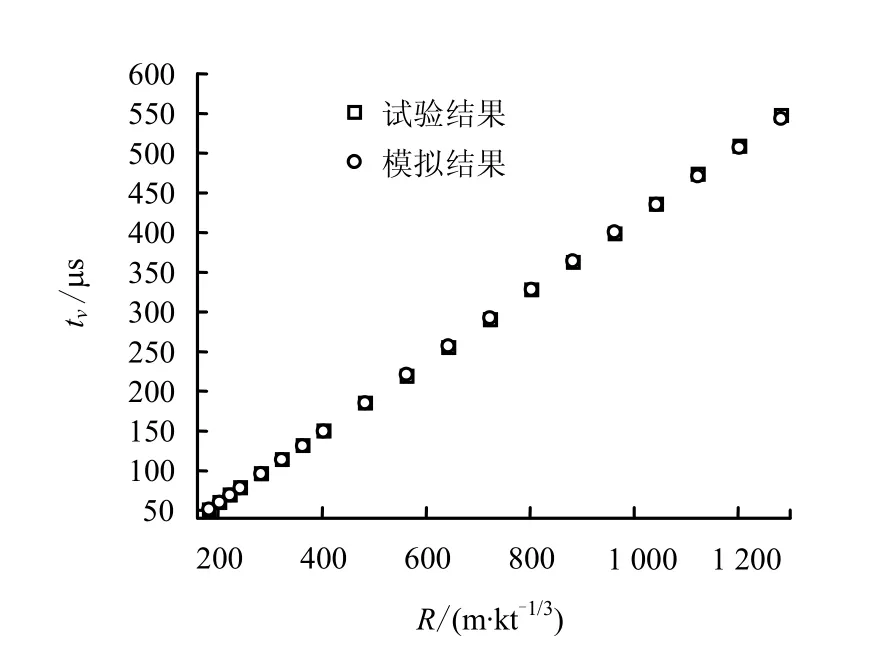
图6 tv随比距离R的变化情况Fig.6 Variations of tv with R

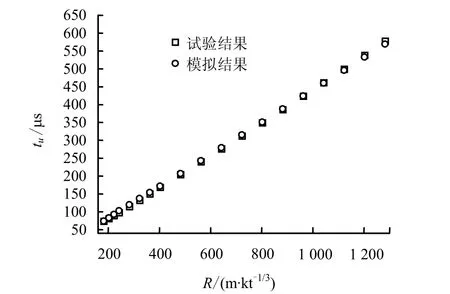
图7 tu随比距离R的变化情况Fig.7 Variations of tu with R

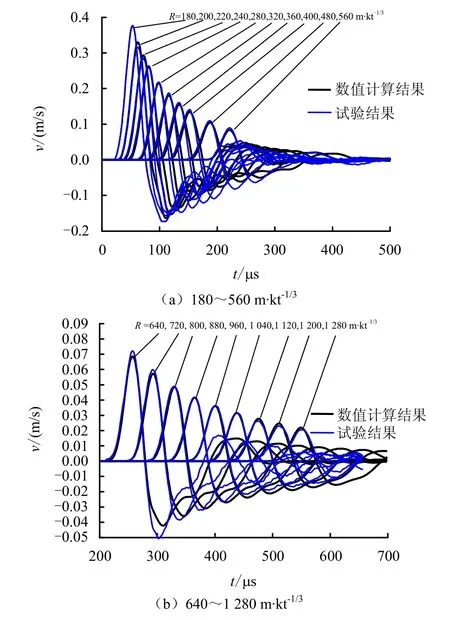
图8 粒子速度模拟曲线与试验曲线的对比Fig.8 Comparison between simulated and experimental curves of particle velocities

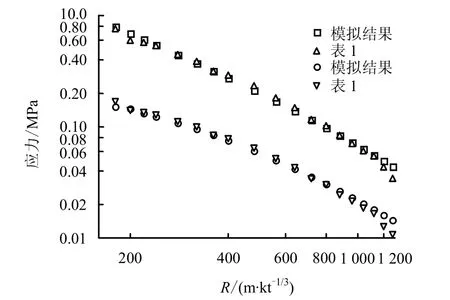
图9 径向应力σ r和切向应力σ θ 随比距离R的变化Fig.9 Variations of radial stress σ r and tangential stress σ θ vs. R

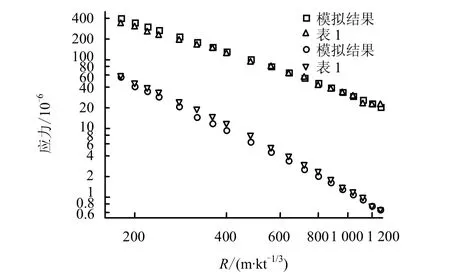
图10 径向应变ε r和切向应变ε θ 随比距离R的变化Fig.10 Variations of radial strain ε r and tangential strain ε θ vs. R

5 结 论

（1）基于变模量模型假定确定了黄土中粒子速度幅值时刻对应的σr、σθ、εr、εθ，从εr和εθ的变化能够看出，随着球面波传播距离的增加，介质的应变状态趋于一维应变状态；同时还确定了黄土的弹性模量E=(1.927±0.216)GPa、体积模量K=(1.284±0.144)GPa、剪切模量G=(0.771±0.086)GPa。

（2）利用反演出的黄土力学量E、K、G作为基本参数，以 ZWT线黏弹性本构为假定，通过对定义的误差函数式（9）取极小值的方式确定了黄土的 ZWT线黏弹性本构参数Ga=0.64 GPa（GM=0.13 GPa）、θM=21 µs。

（3）利用上述参数反演方法给出的黄土黏弹性参数进行数值模拟，模拟结果与试验结果吻合程度较好。另外，基于变模量模型确定的粒子速度幅值时刻对应的σr、σθ、εr、εθ与数值模拟结果也进行了对比，可以看出，两种方法给出的应力和应变有较好的相容性。

[1]崔伟华. 黄土非线性本构模型参数反演[D]. 西安: 西北工业大学, 2004.

[2]马君伟, 李保雄, 慕青松, 等. 马兰黄土黏性的试验研究与模型分析[J]. 岩石力学与工程学报, 2008, 27(增刊1): 3147－3152.MA Jun-wei, LI Bao-xiong, MU Qing-song, et al.Experimental study and model analysis of viscosity of Malan loess[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(Supp.1): 3147－3152.

[3]SONG B, CHEN W, LUK V. Impact compressive response of dry sand[J]. Mechanics of Materials, 2009,41(6): 777－785.

[4]SONG B, CHEN W. Dynamic stress equilibration in split Hopkinson pressure bar tests on soft materials[J].Experimental Mechanics, 2004, 44(3): 300－312.

[5]SONG B, CHEN W. Split Hopkinson pressure bar techniques for characterizing soft materials[J]. Latin American Journal of Solids and Structures, 2005,45(2): 113－152.

[6]SONG B, FORRESTAL M J, CHEN W. Dynamic and quasi-static propagation of compaction waves in a low-density epoxy foam[J]. Experimental Mechanics,2006, 46(2): 127－136.

[7]GRADY D E. Experimental analysis of spherical wave propagation[J]. Journal of Geophysical Research, 1973,78(8): 1299－1307.

[8]LATTER A L, LELERIER R E, MARTINELLI E A, et al.A method of concealing underground nuclear explosions[J]. Journal of Geophysical Research, 1961,66(3): 943－946.

[9]RODEAN H C. Cavity decoupling of nuclear explosions[R]. California: California University, 1971.

[10]SEAMAN L. Lagrangian analysis for multiple stress or velocity gages in attenuating waves[J]. Journal of Geophysical Research, 1974, 45(10): 4303－4314.

[11]王占江, 李孝兰, 张若棋, 等. 固体介质中球形发散波的实验装置[J]. 爆炸与冲击, 2000, 20(2): 103－109.WANG Zhan-Jiang, LI Xiao-Lan, ZHANG Ruo-Qi, et al.An experimental apparatus for spherical wave propagation in solid[J]. Explosion and Shock Waves,2000, 20(2): 103－109.

[12]王占江. 岩土中填实与空腔解耦爆炸的化爆模拟实验研究[D]. 长沙: 国防科学技术大学, 2003.

[13]李孝兰. 空腔解耦爆炸实验研究的理论基础（I）[J]. 爆炸与冲击, 2000, 20(2): 186－192.LI Xiao-lan. Basic theory of decoupled explosions in cavities(I)[J]. Explosion and Shock Waves, 2000, 20(2):186－192.

[14]李孝兰. 空腔解耦爆炸实验研究的理论基础（II）[J]. 爆炸与冲击, 2000, 20(3): 283－288.LI Xiao-lan. Basic theory of decoupled explosions in cavities(II)[J]. Explosion and Shock Waves, 2000, 20(3):283－288.

[15]林英睿. 花岗岩中微药量爆炸应力波传播的 Lagrange分析[D]. 西安: 西北核技术研究所, 2007.

[16]林英睿, 王占江, 李运良, 等. 依球面波粒子速度研究材料本构关系[J]. 解放军理工大学学报(自然科学版),2007, 8(6): 606－610.LIN Ying-rui, WANG Zhan-jiang, LI Yun-liang, et al.Constitutive relation using particle velocity data of spherical waves[J]. Journal of PLA University of Science and Technology, 2007, 8(6): 606－610.

[17]赖华伟, 王占江, 杨黎明, 等. 线性黏弹性球面波的特征线分析[J]. 爆炸与冲击, 2012, 已录待刊.LAI Hua-wei, WANG Zhan-jiang, YANG Li-ming, et al.Characteristics analyses of linear visco-elastic spherical waves[J]. Explosion and Shock Waves, 2012, to be published.

[18]赖华伟, 王占江, 杨黎明, 等. 由球面波径向质点速度实测数据反演材料粘弹性本构参数[J]. 高压物理学报,2012, 已录待刊.LAI Hua-wei, WANG Zhan-jiang, YANG Li-ming, et al.Inversion of constitutive parameters for visco-elastic materials from radial velocity measurements of spherical wave experiments[J]. Chinese Journal of High Pressure Physics, 2012, to be published.

[19]卢强, 王占江, 郭志昀, 等. 基于 ZWT方程的线粘弹性球面波分析[J]. 应用物理, 2012, 3(2): 148－154.LU Qiang, WANG Zhan-jiang, Guo Zhi-yun, et al.Analysis of linear visco-elastic spherical wave based on ZWT constitutive equation[J]. Applied Physics, 2012,3(2): 148－154.

[20]卢强, 王占江, 门朝举, 等. 塑性区沟槽对爆炸应力波屏蔽效应研究[J]. 岩石力学与工程学报, 2012, 31(增刊2), 已录待刊.LU Qiang, WANG Zhan-jiang, MEN Chao-ju, et al.Experimental research on the shielding effects of the gap in plastic zone for the blasting stress wave[J]. Chinese Journal of Rock Mechanics and Engineering, 2012,31(Supp.2), to be published.

[21]王礼立. 应力波基础[M]. 北京: 国防工业出版社,2005.