非饱和土毛细滞回与变形耦合弹塑性本构模型

马田田，韦昌富，陈 盼，魏厚振，伊盼盼

（1.中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室，武汉 430071；2. 武昌理工学院，武汉 430223）

1 引 言

在分析非饱和土问题时，通常将水力学和力学性质分开考虑。但试验现象表明，非饱和土中渗流与变形存在复杂的耦合作用[1－2]。渗流过程影响土体的强度与变形，例如反复的干、湿循环会使非饱和土的强度降低[3]。同时，土体的变形又会改变非饱和土的土-水特性，从而影响孔隙水的渗流过程[4]。因此，有效地模拟任意含水率变化路径下非饱和土的渗流、变形及强度变化之间的耦合作用是亟需解决的关键问题。要解决该关键问题首先需要建立两个本构方程，即应力-应变关系和土-水特征关系及其之间的相互影响。

Alonso等[5]在修正剑桥模型的基础上，提出BBM（Barcelona Basic Model）[6]模型。该模型采用双应力变量，引入 LC（Loading-Collapse）屈服面概念来考虑吸力对屈服应力的硬化作用，能够模拟非饱和土吸水湿陷现象。采用 SI、SD屈服面来描述饱和度的塑性屈服。Wheeler等[7]用吸力控制的非饱和土等向压缩和三轴试验数据验证了BBM模型的合理性。Wheeler[8]、Nuth[9]、孙德安[10]、缪林昌[11]和盛岱超等[12]在BBM模型基础上，采用有效应力代替净应力作为应力状态变量，也用LC屈服面描述非饱和土在不同应力下的吸水湿陷现象。

Wheeler等[7]指出，BBM等非耦合本构模型不能预测在常吸力下饱和度随着剪切而发生变化的特性，也不能反映饱和度随变形的发展增大的这种耦合特性。因此，不能准确地预测不排水条件下非饱和土的水力和力学性状。BBM模型及其以此为基础发展的模型，以塑性体变为硬化参数，因此，不能反映当塑性体变不变时，吸湿即基质吸力减小使屈服面缩小的现象[8]。

在描述非饱和土的本构行为时，目前最流行的做法是基于“LC曲线”提出的模型，用来反映屈服应力随吸力的硬化作用。为了反映土体塑性变形中的非饱和效应，LC曲线（加载-崩塌）已成为许多传统非饱和土本构模型的核心组成部分[2,5－7,13]。

但研究发现，基于LC屈服面的模型有以下局限性[14]：①该类模型在含水率循环变化时不适用，如在饱和与非饱和状态的转换区域附近，如果土体处于脱湿过程且基质吸力小于进气值，可视为饱和土；如果土体处于吸湿过程，则表现出明显的非饱和特性；②LC曲线只是描述屈服强度随吸力增加而增大的性质，而没有引入饱和度作为基本变量，因此，不能考虑前期含水率及其变化历史的影响[8]。由于存在毛细滞回效应，即使在吸力相同的情况下，饱和度并不相同，土体表现出完全不同的力学特性；③模型中没有考虑毛细循环滞回特性；④没有考虑饱和度及其循环变化和土体变形及强度变化之间的耦合效应[8]。

目前主要有两种方式考虑吸力对前期固结压力的硬化作用，韦昌富[14]、Khalili[15]和 Tamagnini[16]等在原本的硬化函数基础上乘以一个受吸力影响的系数，此种方法可以描述吸力的影响与体积硬化作用两者的耦合效应，其中韦昌富[14]是将吸力改为饱和度，未考虑吸力的影响；Jommi[17]、Li[18]则认为，吸力对土体应变硬化有一个附加作用，将吸力的影响与体变硬化的作用分别考虑，总的硬化函数等于两者之和。

Loret等[19]分析试验数据提出以式（1）表示吸力对前期固结压力的硬化作用，

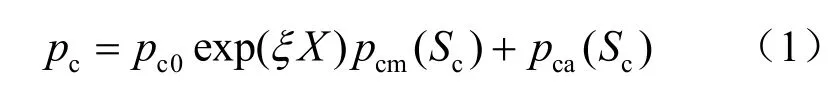
式中：pc为非饱和土的屈服应力；pc0为饱和土的初始屈服应力；X为硬化参数；ξ为系数；pcm(Sc)、pca(Sc)为吸力对前期屈服应力的贡献，Sc为基质吸力； pcm(Sc)=1为体应变硬化与吸力影响之间是解耦的， pca(Sc)=1为体应变硬化与吸力影响是耦合的。但上述模型都没有考虑饱和度和基质吸力同时对初始屈服应力的贡献。

Wheeler[20]、Mualem[21]通过试验发现，饱和度对非饱和土的应力-应变关系有很大的影响，建议在非饱和土弹塑性本构模型中引入循环土-水特征曲线，来描述含水率循环变化对非饱和土变形的影响。

在描述土-水特征曲线时，所见模型主要分为4种：经验模型、区域模型[21]、理性外推模型[22]和边界面模型[23]。尽管这些模型不同程度地考虑了毛细滞回现象，但很少反映土体变形对持水特征的影响。缪林昌[24]、方祥卫[25]、龚壁卫等[26]通过试验研究了土体的密实状态对土-水特征关系的影响，Gallipoli[27]通过试验提出了土体体变与 van Genuchten模型[28]参数的关系，因此，可以考虑体变对土-水特征曲线的影响。基于以上存在的问题，本文将吸力和饱和度同时作为硬化参数，在同一个框架中建立了塑性变形和毛细滞回耦合的本构模型。

2 非饱和土毛细滞回与骨架变形耦合本构模型

2.1 应力状态变量

应力状态变量采用Bishop[29]有效应力σi′j和基质吸力Sc：

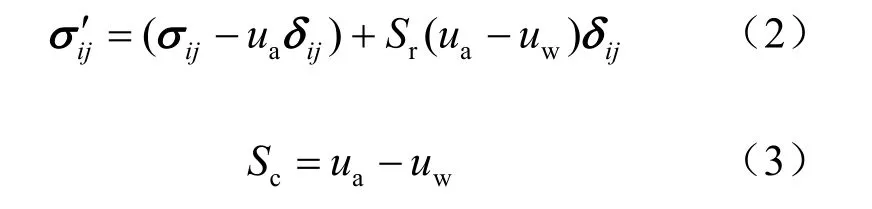
在三轴应力状态下：

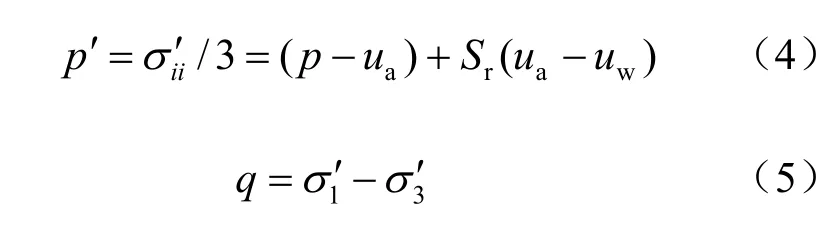
式中：σij为总应力张量；σi′j为有效应力张量；Sr为饱和度；ua、uw分别为孔隙气压力和孔隙水压力；δij为单位张量。式（1）是将Bishop有效应力[29]中的参数χ取为饱和度Sr[15]。Houlsby[30]提出与此应力状态变量（σi′j，Sc）功共轭的应变为（εij，Sr），其中εij为应变张量。p′为平均有效应力；q为广义剪应力；p为平均总应力。

2.2 基质吸力和饱和度对屈服应力的作用

在达到相同吸力的条件下，分别通过吸湿和脱湿之后的土样含水率的大小、分布可能并不相同，如图1所示。从非饱和土的CT扫描图[31－32]可以看出，相同含水率条件下，孔隙水的分布状态是不同的，经历吸湿过程的土样比经历脱湿过程的含水率分布更加均匀，因此，非饱和土的力学性质也不同。通过测量两种状态试样的压缩波传播时发现，前者的压缩波速明显比后者小[31,33－34]。

图1 非饱和土的CT扫描图（饱和度均为92%时分别经过吸湿和脱湿而成的土样）Fig.1 CT images of unsaturated soil(degree of saturation is 92%, after drying and wetting respectively)

从上面的分析可知，由于毛细滞回的影响，非饱和土体的土-水状态与土体所经历的水力状态密切相关，而土-水状态的变化必将影响土体的强度与变形。因此，必须要同时考虑基质吸力和饱和度对前期固结压力的影响。通过试验[35]发现，屈服应力随着吸力的增加、饱和度的减小而增大，因此，假设用式（6）来考虑吸力和饱和度对屈服应力的硬化作用，

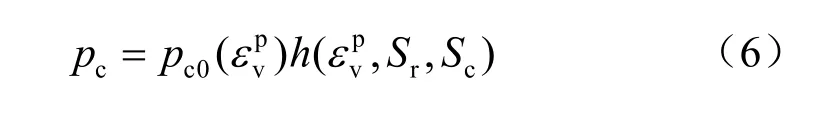
采用类似Alonso[5]提出的压缩曲线的斜率与吸力的关系，定义h函数为

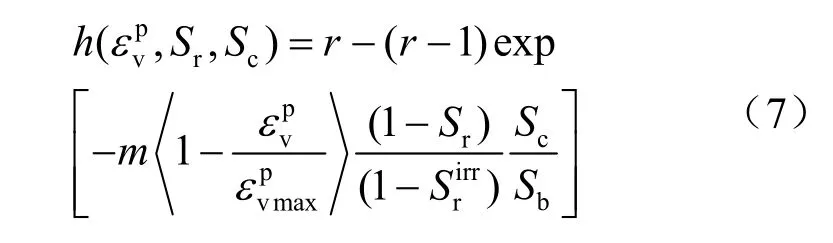
式中：r为非饱和土处于残余饱和度时的强度与饱和土屈服强度的比值；m为屈服应力随饱和度和吸力增长的速度；为最大的塑性体积应变；为残余饱和度；Sb为非饱和土的进气值； Sc/Sb为吸力比。〈 〉为Macauley大括号，定义为 x = xH(x)，其中H(x)为Heaviside公式。

式（7）满足以下条件：①当 Sr= 100%和Sc=0时，h=1.0；②随着Sr的减小，Sc的增大而增大，并趋于一个稳定值；③随着的增大，饱和度和基质吸力对强度的影响逐渐减弱，当趋于最大值即时，饱和度和基质吸力不再对强度有影响。

本文采用修正剑桥模型[36]，如图2所示，屈服函数为

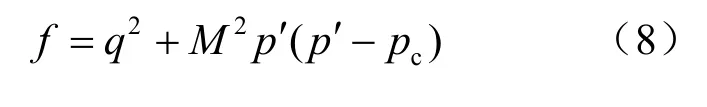
式中：f为屈服函数；M为临界状态线的斜率。

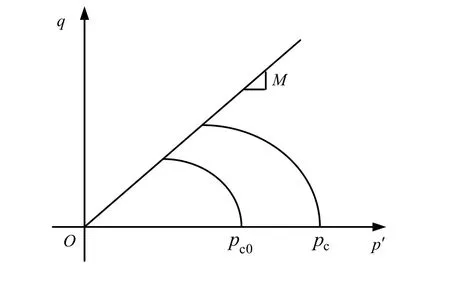
图2 修正剑桥模型的屈服面Fig.2 Yield surfaces of modified Cam-clay model

图中饱和土的屈服应力pc0是塑性体变的函数。非饱和土的屈服应力pc是塑性体变、饱和度、基质吸力的函数。

弹性变形和塑性变形分别为

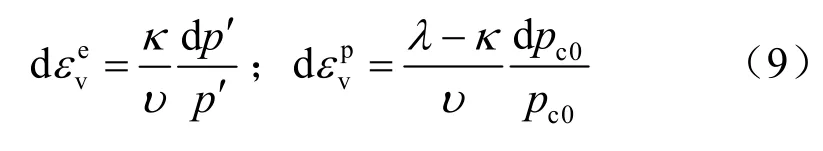
式中：λ、κ为初始压缩曲线的斜率和回弹斜率；υ为土体比容积。

采用相关流动法则

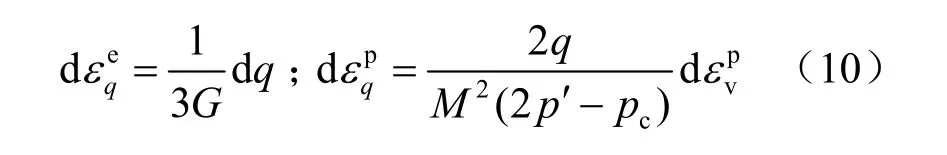
式中：G为土体的剪切模量。硬化准则为

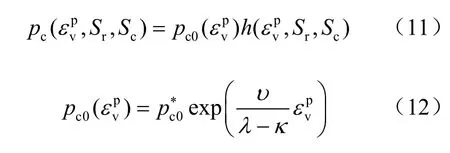
从前面的推导得出，吸力和饱和度对屈服应力的硬化作用如图3所示。图中实线为脱湿时基质吸力对前期屈服应力的影响，虚线为吸湿时基质吸力对前期屈服应力的影响，图上的数据点为Wheeler[7]所做的试验。从图上可以看出，当基质吸力相同时，由于存在滞回效应，脱湿对应的饱和度比吸湿时高，所以相应的屈服应力较吸湿时小，而且含水率分布较不均匀，这点与前面提出的饱和度的作用相对应。

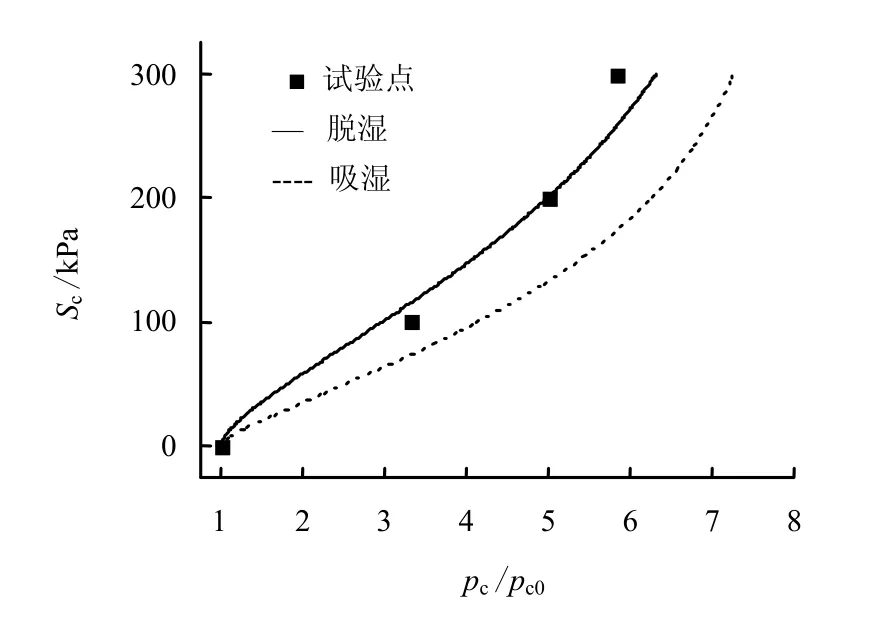
图3 模型得出的LC曲线与试验数据的对比Fig.3 Comparison between simulated LC curves and tested data

从上面的分析可以看出，尽管没有将基质吸力当作独立变量来考虑，但推导得出的LC曲线与试验数据拟合结果良好。

2.3 变形对土-水特征关系的影响

Wei等[37]严格以内变量热动力学和多孔介质理论为基础，提出了一个简单实用的毛细滞回内变量模型。该模型基于多相、多孔介质理论，将毛细循环现象视为一个非饱和土的能量耗散过程。在循环边界曲线给定的情况下，该模型只需一个参数就能确定任意含水率变化路径下非饱和土的土-水特征关系。该模型改进后可以考虑体变对土水特征关系的影响。

该模型以Feng等[38]提出的土-水特征曲线为边界线

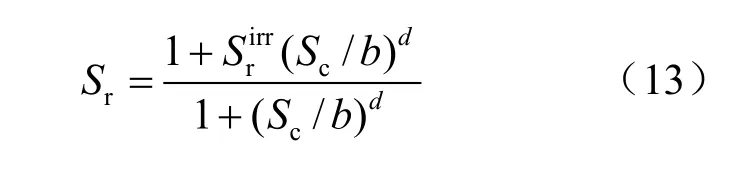
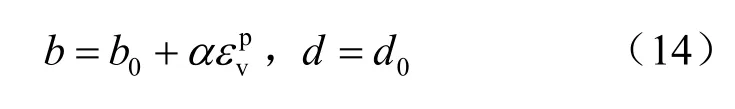
式中：b、d、b0、d0、α为材料参数，与土体的土-水状态相关，在脱湿和吸湿时取不同值。

当不考虑变形的影响时，基质吸力与饱和度变化关系为

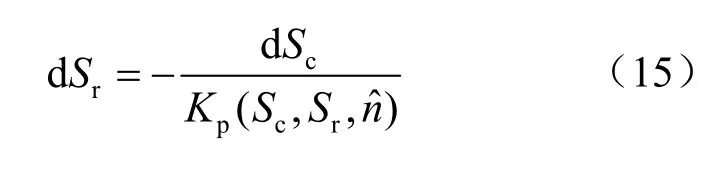
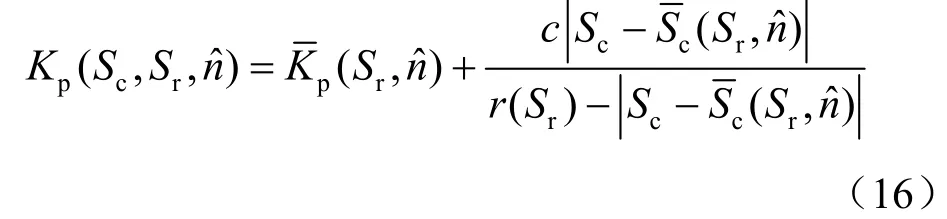
通过试验发现，土体的孔隙比对土-水特征曲线有重要影响[39]，孔隙比减小时，进气值增大，土-水特征曲线向右移动。

考虑变形对土-水特征曲线的影响，有

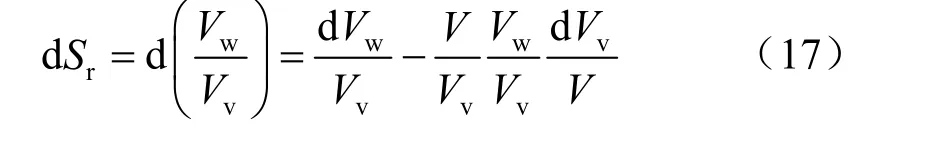
式中：Vw、Vv分别为水和孔隙的体积；等号右边第1项表示基质吸力对饱和度的影响，第2项描述变形对饱和度变化的影响。忽略弹性变形的影响，式（17）可以变为

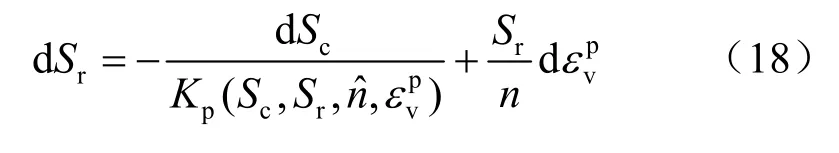
式中：n为孔隙率；第2项表示毛细滞回与变形的耦合效应。

3 模型验证

3.1 各向同性压缩和吸湿试验

采用孙德安[40]的各向同性加压湿陷试验来验证所提出的模型。试样采用属于粉质黏土的珍珠黏土（pearl clay），非饱和击实样。此黏土的液限为49%，塑限为22%，土粒相对密度为2.71，初始含水率为26%。图4为模型模拟的结果与试验数据对比图。应力路径为从 A点（ pnet=20 kPa，Sc=147 kPa）保持吸力为常数加载到 B点（pnet=98 kPa， Sc= 147 kPa），然后保持净应力不变，进行吸湿试验，到达 C点（ pnet=98 kPa,Sc=0 kPa），最后土样在 0吸力下各向同性压缩至196 kPa。其中pnet为平均净应力， pnet=p-ua。图上从A点到B点和C点到D点为各向同性压缩，B点到C点为吸湿路径，当吸力减小时，屈服应力降低。类似地，另外一条路径从 pnet= 196 kPa 开始吸湿。从图上可以看出，尽管吸湿时有效应力降低，但屈服应力也在减小，土体的塑性变形大于回弹体变，因此，发生了湿陷现象。

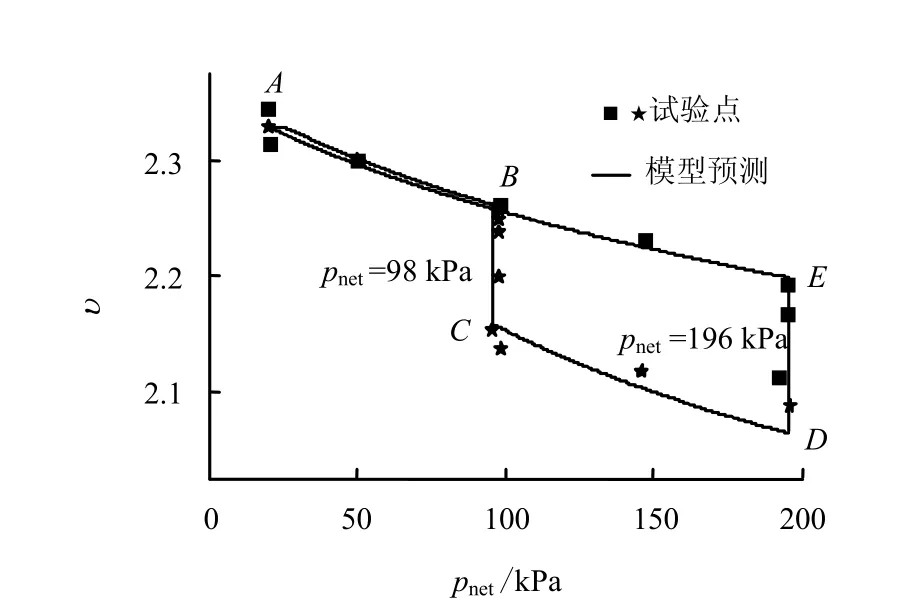
图4 净应力与比容积的关系Fig.4 Relation between net stress and specific volume

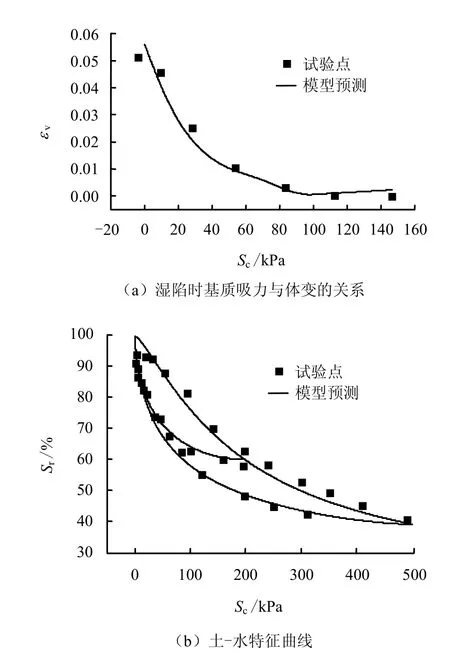
图5 基质吸力与湿陷变形的关系和SWCC曲线Fig.5 Relation between matric suction and deformation and SWCC

图6为当 Sc= 147 kPa时各向同性压缩之后，在时进行吸湿。图中是饱和度随平均净应力的变化关系，因为有塑性应变发生，饱和度随着净应力增大而略微增大。这是由于塑性变形使孔隙比减小造成的。

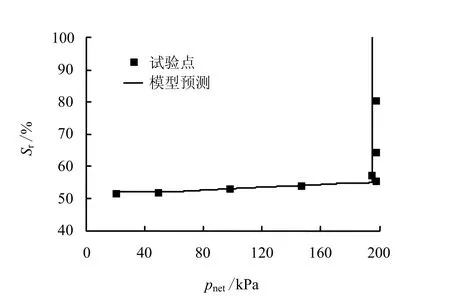
图6 饱和度随净应力的变化关系Fig.6 Variation of saturation with net stress

图7为土样在给定的平均净应力下经过吸湿和脱湿之后的比容积变化，从图可以看出，土体在吸湿阶段会产生弹性膨胀，而在脱湿阶段则表现出明显塑性收缩现象，这与Sharma[3]得出的结论相一致。

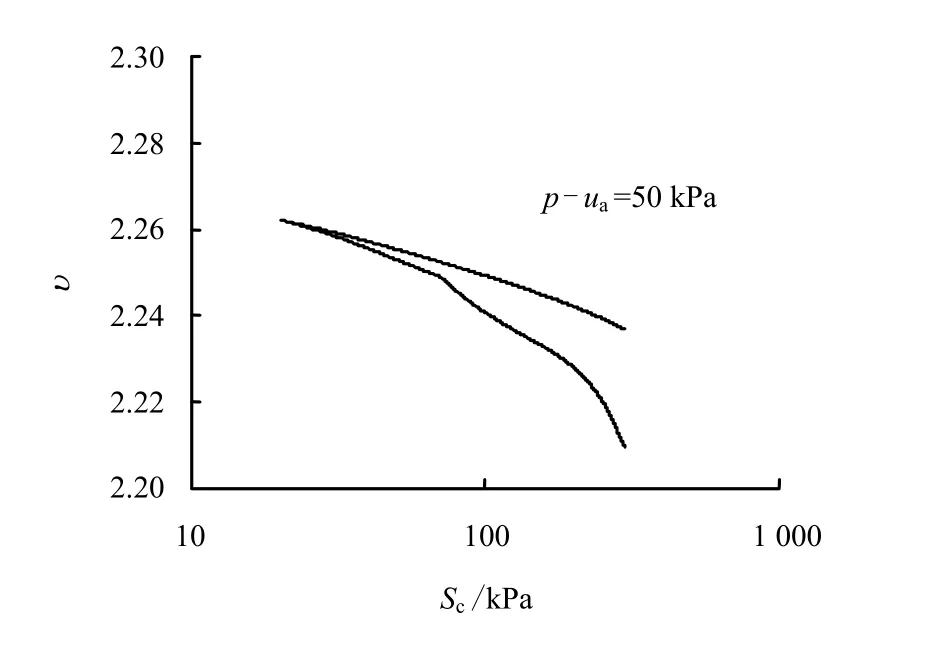
图7 模型对吸湿、脱湿循环中比容积变化的模拟Fig.7 Specific volume change obtained by simulation under of wetting and drying cycles

3.2 常净应力和常吸力下的剪切试验

采用孙德安[1]所做的非饱和土三轴试验结果进行模拟。根据试验结果，得出pearl clay的力学参数为 λ=0.12，κ=0.03， pc0= 70 kPa，r=4.5，m= 3.65，=0.15，G= 8 MPa。

土 样 在 pnet= 196 kPa 、 Sc= 147 kPa时 ，q= 0 → 296 kPa加载至破坏。图8～11为试验结果和模型模拟的对比。图8为体变εv与主应变ε1之间的关系。图9、11为主应力比 σ1/σ3与主应变ε1、ε3之间的关系。图 10为 σ1/σ3与饱和度Sr之间的关系，图上初始的直线段表示土样为弹性状态，与前面忽略弹性体变对饱和度的影响假设相一致。从图9、11中可以看出，模型得出第一主应变较小，第三主应变较大，与试验数据有偏差，但总体上的趋势是相一致的。图 10中的直线段为初始的弹性变形，对饱和度没有影响。

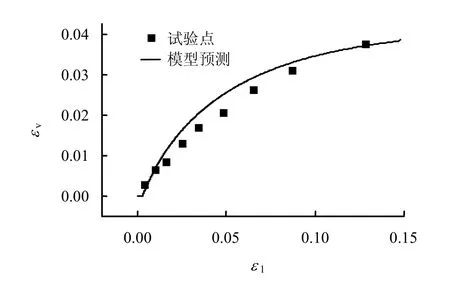
图8 第一主应变与体变的试验结果与模型预测Fig.8 Test and prediction results of maximum principal strain and volume strain

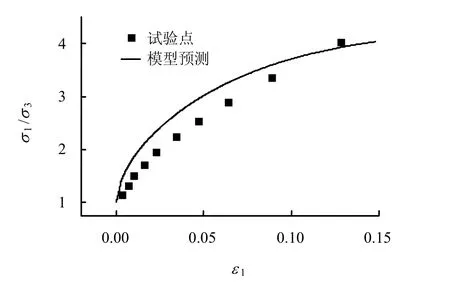
图9 第一主应变与主应力比的试验结果与模型预测Fig.9 Test and prediction results of maximum principal strain and ratio of principal stresses

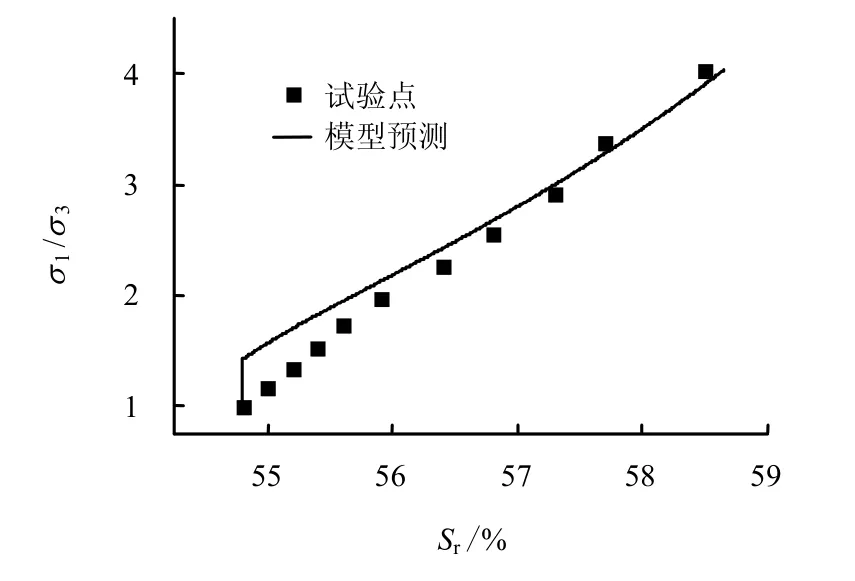
图10 饱和度与主应力比的试验结果与模型预测Fig.10 Test and prediction results of saturation and ratio of principal stresses

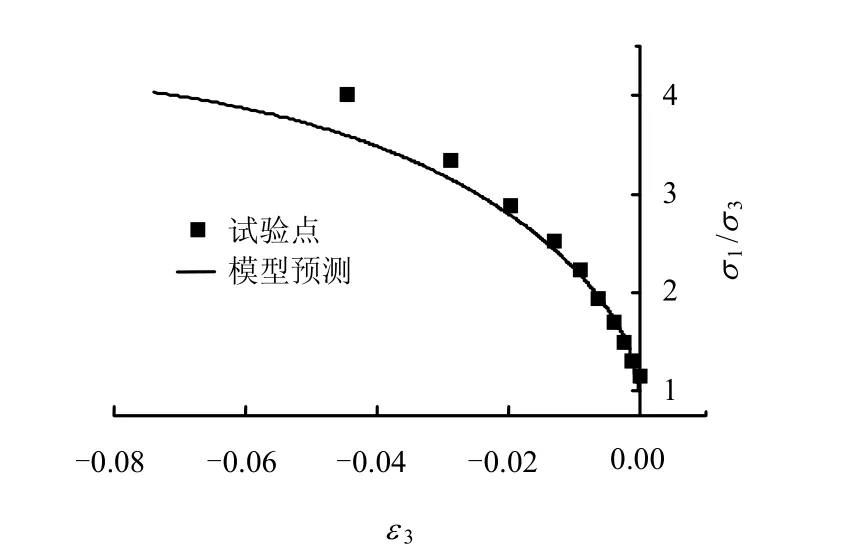
图11 第三主应变与主应力比的试验结果与模型预测Fig.11 Test and prediction results of minor principal strain and ratio of principal stresses

3.3 体变对土-水特征曲线的影响

土体发生体变时，孔隙比降低，进气值增大，因此，使得土-水特征曲线向外移动。模型所得结果如图12所示，从图可以看出，体变对吸湿的影响较脱湿大。这是因为体积压缩导致孔隙变小，大孔隙比例减小，使得大孔隙对小孔隙的阻隔作用减弱，形成的滞回圈变小。

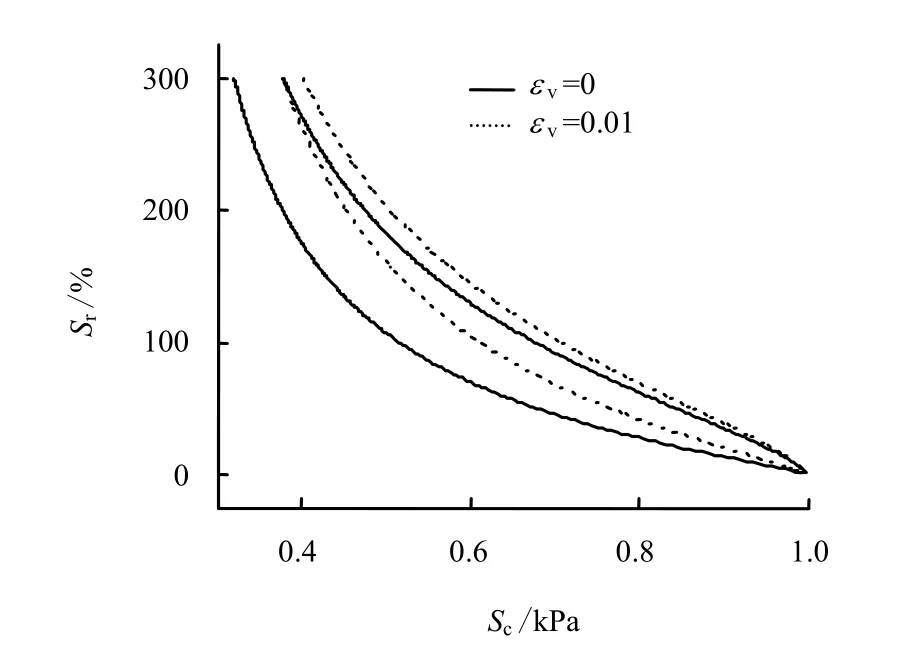
图12 体变对土-水特征曲线的影响Fig.12 Effect of volume strain on soil-water characteristic curves

4 结 论

本文在修正剑桥模型的基础上，考虑了非饱和土的硬化作用建立了毛细滞回与变形耦合的本构模型。该模型摒弃了传统模型的LC曲线，在修正剑桥模型和毛细滞回内变量模型的基础上增加了两个参数考虑基质吸力和饱和度对屈服应力的硬化作用。两个参数可通过试验得出的LC曲线得到。其他参数可通过常规的力学和水力学试验得到。通过与试验结果对比，证明此模型可以模拟基本的非饱和土力学与水力学行为，包括湿陷、强度随基质吸力的增加而增大等。而且同时考虑了体变对土-水特征曲线的影响，毛细滞回及其含水率变化历史对变形的影响。

[1]SUN D A, SHENG D, SLOAN S W. Elastoplastic modelling of hydraulic and stress-strain behaviour of unsaturated soils[J]. Mechanics of Materials, 2007,39(3): 212－221.

[2]WHEELER S J. Inclusion of specific water volume within an elastoplastic model for unsaturated soils[J].Canadian Geotechnical Journal, 1996, 33(1): 42－57.

[3]SHARMA R S. Mechanical behavior of an unsaturated highly expansive clays[D]. Oxford, UK: University of Oxford. 1998.

[4]CHARLES W W N, PANG Y W. Influence of stress state on soil-water characteristics and slope stability[J].Journal of Geotechnical and Geoenvironmental Engineering, 2000, 126(2): 157－166.

[5]ALONSO E E, GENS A, JOSA A. A constitutive model for partially saturated soils[J]. Geotechnique, 1990, 40(3):405－430.

[6]BOLZON G, SCHREFLER B A, ZIENKIEWICZ O C.Elastoplastic soil constitutive laws generalized to partially saturated states[J]. Géotechnique, 1996, 46(2): 279－289.

[7]WHEELER S J, SIVAKUMAR V. An elasto-plastic critical state framework for unsaturated soil[J].Geotechnique, 1995, 45(1): 35－53.

[8]WHEELER S J, SHARMA R S, BUISSON M S R.Coupling of hydraulic hysteresis and stress-strain behaviour in unsaturated soils[J]. Geotechnique, 2003,53(1): 41－54.

[9]NUTH M, LALOUI L. Advances in modelling hysteretic water retention curve in deformable soils[J]. Computers and Geotechnics, 2008, 35(6): 835－844.

[10]SUN D A, LI X. An elastoplastic hydro-mechanical model for unsaturated soils[C]//Proceedings of the 7th International Conference on Computational Science, Part III: ICCS. Beijing: Springer-Verlag, 2007: 1138－1145.

[11]缪林昌. 非饱和土的本构模型研究[J]. 岩土力学, 2007,28(5): 855－860.MIAO Lin-chang. Research of constitutive model of unsaturated soils[J]. Rock and Soil Mechanics, 2007,28(5): 855－860.

[12]SHENG D, GENS A, FREDLUND D G, et al.Unsaturated soils: From constitutive modelling to numerical algorithms[J]. Computers and Geotechnics,2008, 35(6): 810－824.

[13]CUI Y J, DELAGE P. Yielding and plastic behaviour of an unsaturated compacted silt[J]. Geotechnique, 1996,46(2): 291－311.

[14]韦昌富, 李幻, 王吉利. 考虑弹塑性变形和毛细循环滞回的非饱和土本构模型[C]//第一届全国岩土本构理论研讨会论文集. 北京: 北京航空航天大学, 2008: 259－266.

[15]KHALILI N, GEISER F, BLIGHT G E. Effective stress in unsaturated soils: Review with new evidence[J].International Journal of Geomechanics, 2004, 4(2):115－126.

[16]TAMAGNINI R. An extended Cam-clay model for unsaturated soils with hydraulic hysteresis[J].Geotechnique, 2004, 54(3): 223－228.

[17]JOMMI C. Remarks on the constitutive modelling of unsaturated soils[C]//Experimental Evidence and Theoretical Approaches in Unsaturated Soils. Rotterdam:A. A. Balkma, 2000: 139－153.

[18]LI X S. Thermodynamics-based constitutive framework for unsaturated soils 2: A basic triaxial model[J].Geotechnique, 2007, 57(5): 423－435.

[19]LORET B, KHALILI N. A three-phase model for unsaturated soils[J]. International Journal for Numerical and Analytical Methods in Geomechanics,2000, 24(11): 893－927.

[20]WHEELER S J. An alternative framework for unsaturated soil behavior[J]. Geotechnique, 1995, 41(2): 257－260.

[21]MUALEM Y. A conceptual model of hysteresis[J].Water Resources Research, 1984, 10(3): 514－520.

[22]PARLANGE J Y. Capillary hysteresis and the relationship between drying and wetting curves[J]. Water Resources Research, 1976, 12(2): 224－228.

[23]LI X S. Modelling of hysteresis response for arbitrary wetting/drying paths[J]. Computers and Geotechnics,2005, 32(2): 133－137.

[24]MIAO L C, JING F, HOUSTON S L. Soil-water characteristic curve of remolded expansive soils[J].Geotechnical Special Publication, 2006, 147(1): 997－1004.

[25]方祥位, 陈正汉, 申春妮, 等. 剪切对非饱和土土-水特征曲线影响的探讨[J]. 岩土力学, 2004, 25(9): 1451－1454.FANG Xiang-wei, CHEN Zheng-han, SHEN Chun-ni.et al. A study of effect of shear on soil-water characteristic curve of an unsaturated soil[J]. Rock and Soil Mechanics, 2004, 25(9): 1451－1454.

[26]龚壁卫, 吴宏伟, 王斌. 应力状态对膨胀土SWCC的影响研究[J]. 岩土力学, 2004, 25(12): 1915－1918.GONG Bi-wei, WU Hong-wei, WANG Bin. Influence of stress states on soil-water characteristics of expansive soils[J]. Rock and Soil Mechanics, 2004, 25(12): 1915－1918.

[27]GALLIPOLI D, WHEELER S J, KARSTUNEN M.Modelling the variation of degree of saturation in a deformable unsaturated soil[J]. Géotechnique, 2003,53(1): 105－112.

[28]GENUCHTEN M T V. A closed-form equation for predicting the hydraulic conductivity of unsatutated soils[J]. Soil Science Society of America Journal, 1980,44(5): 892－898.

[29]BISHOP A W. The principle of effective stress[J].Teknisk Ukeblad, 1959, 106(39): 113－143.

[30]HOULSBY G T. The work input to an unsaturated granular material[J]. Geotechnique, 1997, 47(1): 193－196.

[31]CADORET T, MARION D, ZINSZNER B. Influence of frequency and fluid distribution on elastic wave velocities in partially saturated limestones[J]. Journal of Geophysical Research, 1995, 100(B6): 9789－9803.

[32]CADORET T, MAVKO G, ZINSZNER B. Fluid distribution effect on sonic attenuation in partially saturated limestones[J]. Geophysics, 1998, 63(1): 154－160.

[33]KNIGHT R, NOLEN-HOEKSEMA R. A laboratory study of the dependence of elastic wave velocities on pore scale fluid distribution[J]. Geophysical Research Letters,1990, 17(10): 1529－1532.

[34]RAVALEC L M, GUEGUEN Y, CHELIDZE T. Elastic wave velocities in partially saturated rocks: Saturation hysteresis[J]. Journal of Geophysical Research, 1996,101(B1): 837－844.

[35]SUN D A, MATSUOKA H, CUI H B, et al.Three-dimensional elasto-plastic model for unsaturated compacted soils with different initial densities[J].International Journal for Analytical and Numerical Methods in Geomechanics, 2003, 27(12): 2079－2098.

[36]ROSCOE K H, BURLAND J B. On the generalized stress-srain behavior of wet clay[C]//Engineering Plasticity. Cambridge: Cambridge University Press, 1968:535－609.

[37]WEI C F, DEWOOLKAR M M. Formulation of capillary hysteresis with internal state variables[J]. Water Resources Research, 2006, 42(7): W07405. 1－16.

[38]FENG M, FRELUND D G. Hysteresis influence associated with thermal conductivity sensor measurements[C]//The 52nd Canadian Geotechnical Conference and Unsaturated Soil Group, Proceedings from Theory to the Practice of Unsaturated Soil Mechanics, Regina, Saskatchewan, Canada: [s. n.], 1999:651－657.

[39]VANAPALLI S K, FREDLUND D G, PUFAHL D E.The influence of soil structure and stress history on the soil-water characteristics of a compacted till[J].Geotechnique, 1999, 49(2): 143－158.

[40]SUN D A, SHENG D, XU Y. Collapse behavior of unsaturated compacted soil with different initial densities[J]. Canadian Geotechnical Journal, 2007,44(6): 673－686.