基于藤结构Copula的多元信用风险相关性度量模型及其比较
罗长青,欧阳资生
(1.湖南商学院 财政金融学院,湖南 长沙 410082; 2.湖南大学 工商管理学院,湖南 长沙 410082)*
一、引 言
现代金融信用风险具有易传染性特征,信用风险的爆发往往呈现出非线性扩散的现象,当信用风险事件处于不可控制的状态时,以商业银行为中枢的金融体系乃至经济体系会面临较大的系统性风险,如若应对不力,便会爆发金融危机和经济危机。商业银行如果只考虑单一的信用风险事件已经不能适应外部复杂的经营环境变化,“你中有我,我中有你”的信用风险相关或传染,使得考虑信用风险之间的相关性,特别是极端风险事件下的相关性,实施信贷组合管理成为了商业银行风险管理的一种发展趋势。随着Basel II的正式公布,有关信用风险相关性度量模型的构建及管理的专业技巧,已成为商业银行和其他金融机构十分重视的议题。
由于信贷组合管理越来越受到重视,国内外学者开始对信用风险相关性进行了理论和实证上的探讨。Wu在度量一篮子信用组合风险的过程中运用了因素Copula模型[1]。Crook和 Moreira则运用Copula函数,使用不对称相关性对信用组合的风险进行了分析[2]。刘久彪以预期短缺ES度量信用组合风险,利用t–copula建模债务人的风险相关性,提出了一种确定信用组合一致性风险量度ES的方法[3]。詹原瑞、韩铁和马珊珊以及童中文和何建敏分别运用不同的Copula函数对信用衍生产品中的违约风险相关性进行了建模,并通过模拟的方式验证了模型的有效性和可实现性[4,5]。苏静和杜子平结合Copula函数与KMV模型相结合对商业银行组合信用风险进行了度量[6]。彭建刚和吕志华提出了行业风险因子之间是相互关联的Credit Risk+模型[7]。梁凌、彭建刚和王修华建立了抵押品池综合违约损失率的计算模型[8]。熊正德和冷梅则对信用风险传染现象进行了描述[9]。已有研究大多运用二元Copula模型,从模拟角度或实证角度对信贷资产的信用风险二元相关性进行了探讨,而对信贷资产高维相关性的探讨相对较少。
在商业银行信贷风险管理以及在信贷资产证券化过程中,信贷资产通常是多元的,二维Copula模型虽然能够在一定程度上描述信贷组合的风险状况,但并不能描述多资产的相依结构,因此需要引入高维Copula模型。然而,高维Copula模型在构建过程中参数较多、计算复杂。本文引入Bedford和Cooke提出的藤结构分解模式[10,11],对多元 Copula模型来进行分解和参数估计,从而实现对多元信用风险相关性的建模。
二、行业信用风险的度量及藤结构设定
以行业分析为基础来构建和优化信贷组合既能满足信贷组合管理的要求,又能提高管理的效率,也符合当前国内外商业银行管理的现实状况。而以行业为基础来构建信用风险相关性度量模型,首先需要构建行业信用风险指数,而对行业信用风险指数的构建需要对单个企业的信用风险进行评价,本文运用组合评价模型来评估单个企业的信用风险,限于文章篇幅,在此只描述模型构建思路(参见图1)。以企业首次被ST作为违约事件发生的标志,选择深、沪两交易所首次被进行特别处理的ST公司,同时在同行业中选取资产最为接近的非ST公司作为配对样本进行建模。上市公司的行业分别为电力、煤气及水的生产和供应业,批发和零售贸易业,石油、化学、塑胶、塑料业,信息技术业等4个行业,它们分别作为强周期型行业、防御型行业、弱周期型行业以及成长型行业的代表,分别以第I,II,III和第IV类行业来表示。各类模型的权重参数(w1,w2,w3)如表1所示。本文参考刘盛宇等人的研究,建立组合预测模型[12]。

图1 信用风险组合评价模型的构建思路
从总的预测精度来看(如表1所示),相对于MDA模型、SVM模型以及KMV模型,Hybrid模型的预测精度较高,除电力、煤气及水的生产和供应业,食品饮料行业以外,其它行业的预测准确率均超过了80%,这反映了Hybrid模型在评价企业信用风险,尤其是上市公司信用风险方面具有较好的性能。

表1 Hybrid模型的参数估计结果及预测错误率(分行业)
运用Hybrid模型估算出单个上市公司的违约风险之后,运用下式计算行业信用风险中的指数:
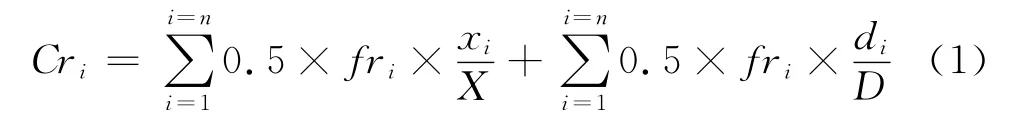
其中,Cri为某一行业的信用风险,xi和X分别为单个企业的总资产和样本企业的总资产之和,n为行业内样本企业的家数,fri为单个企业的信用风险大小。di和D分别为单个企业的负债和样本企业的负债之和。行业信用风险的计算期限为2006年6月~2010年12月,数据周期为2个星期。四大行业的信用风险如图2所示。
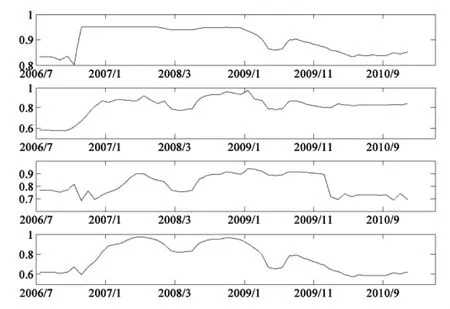
图2 行业信用风险趋势图
考虑到信用风险相关性的非线性和非对称特点,本文采用Copula函数来实现。对于Copula函数的分解模式,则以藤结构的方式来分解。在对多元信用风险相关性度量模型中采用Canonical藤和D藤两类分解结构来实现对多元Copula模型的分解。
三、Canonical藤结构下的参数估计及信用风险相关性度量
Clayton Copula函数能较好地刻画下尾相关的特点,所以,在构建多元Copula函数的过程中,选择以Clayton Copula函数为基准:

分别以DL(电力、煤气及水的生产和供应业)、PF(批发、零售、贸易业)、SH(石油、化学、塑胶、塑料)以及XX(信息技术业)来代表第I,II,III和第IV类行业来构建信用风险相关性度量的多元Copula模型,在Canonical藤分解结构下,多元Copula函数的联合密度函数f(x1,x2,x3,x4)为:
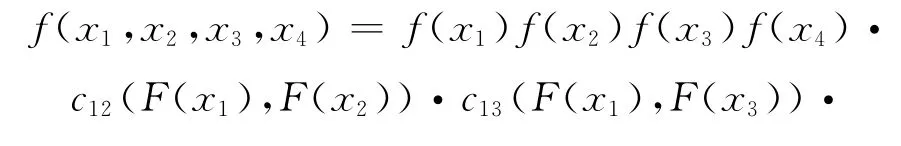
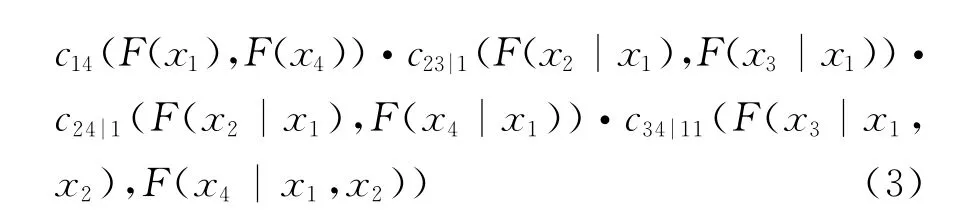
式(3)中的每个Pair Copula密度函数都可以分解为一个二元Copula密度函数和边缘分布密度函数的乘积,如下所示:

条件分布函数F(x|v),可以通过下式来求得:

Canonical藤下的对数似然函数为:

其中,j表示树的个数,i表示每棵树中的结点的个数,θ代表多元Copula密度函数的参数集。
在Canonical藤结构的分解模式下,多元联合密度函数的对数似然函数参数的初值求解过程如下:
步骤1:根据信用风险数据计算多元Copula密度函数的初值:c12((F(x2),F(x1));c13((F(x3),F(x1));c14((F(x4),F(x1))。
步骤2:根据f(x1,x2)=c12(F(x2),F(x1))f(x1)f(x2)以及步骤1中的初值,来计算信用风险的样本数据,其中:
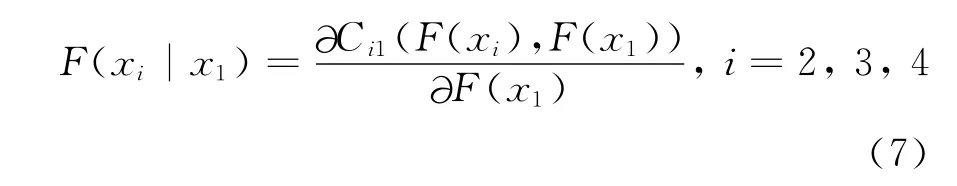
步骤3:利用步骤2中求得的F(x2|x1),F(x3|x1),F(x4|x1)估计第二层次的多元Copula函数的参数值c23|1(F(x2|x1),F(x3|x1));c24|1(F(x3|x1),F(x4|x1))。
步骤4:重复以上步骤,估计Canonical藤结构中的所有参数值(结果参见表2)。

表2 Canonical藤结构下的多元Clayton Copula模型估计
四、D藤结构下的参数估计及信用风险相关性度量
D藤结构的分解模式下,Copula函数的联合密度函数f(x1,x2,x3,x4):
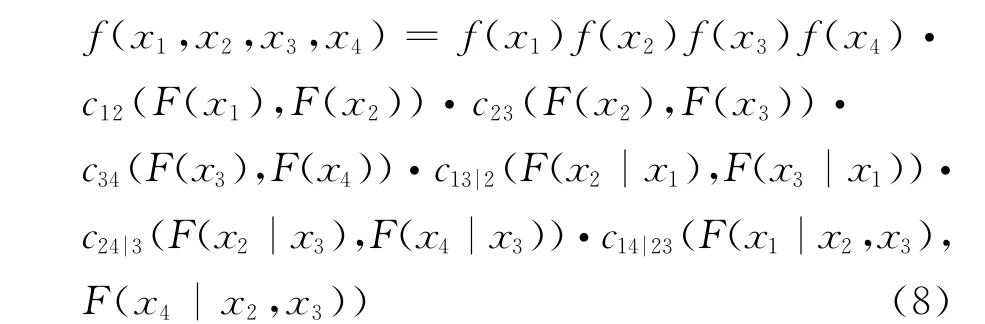
D藤下的对数似然函数为:

其中,j表示树的个数,i表示每棵树中的结点的个数,θ代表多元Copula密度函数的参数集。
D藤结构下的多元联合密度函数的对数似然函数参数的初值求解过程如下:
步骤1:根据信用风险数据计算多元Copula密度函数的初值:c12((F(x2),F(x1));c23((F(x3),F(x2));c34((F(x4),F(x34))。
步骤2:根据f(x1,x2)=c12(F(x2),F(x1))f(x1)f(x2)以及步骤1中的初值,来计算信用风险的样本数据,其中:

步骤3:利用步骤2中求得的F(x2|x1),F(x3|x2),F(x4|x3)估计第二层次的多元Copula函数的参数值c13|1(F(x3|x1),F(x1|x1));c24|3(F(x2|x3),F(x4|x3))。
步骤4:重复以上步骤,估计D藤结构中的所有参数值(结果参见表3)。

表3 D藤结构下的多元Clayton Copula模型估计
五、模型的比较及分析
从模型参数估计的t检验来看,多元Clayton Copula函数的拟合效果较好,两种藤结构的Copula模型都有一定的合理性,为了得到最佳的变量逻辑分解结构,运用AIC和BIC准则来进行检验Canonical藤和D藤分解结构。
当存在某一关键变量作为主导变量时,Canonical藤的统计性能较优,当变量相依结构并不存在主导变量时,则相对适宜用D藤结构的分解模式。将两类模型相比较可以发现,适用于Canonical藤结构的Pair Copula模型的AIC和BIC均小于D藤结构的AIC和BIC。在本文的研究中,Canonical藤结构的根节点为第I类行业,即以电力煤气及水的生产为代表的强周期性行业,第I类行业在行业结构中可能具有引导作用,因此,Pair Copula分解的结构更适合Canonical藤。
六、结论及启示
Canonical藤和D藤多元Clayton Copula模型均能较好地描述多元信用风险相关结构。但两类模型相比较可以发现,适用于Canonical藤结构的多元Clayton Copula模型的拟合优度更好,说明信用风险相关性的产生可能会由某一占主导作用的产业所引致。商业银行和其他金融机构可参考所构建的藤结构Copula模型进行信贷组合管理:(1)可依照藤结构Copula模型对信贷组合中的风险相关或风险传染现象进行风险预警;(2)在藤结构Copula模型估计的基础上,金融机构可以针对多元信贷资产组合进行一致性风险度量;(3)求解出风险最小条件下的最优信贷资产权重,从而为金融机构调整信贷组合的资产比例提供依据。
[1]Wu Po Cheng.Applying a factor copula to value basket credit linked notes with issuer default risk[J].Finance Research Letters,2010,7(3):178-183
[2]Crook Jonathan,Moreira Fernando.Checking for asymmetric default dependence in a credit card portfolio:a copula approach[J].Journal of Empirical Finance,2011,18(4):728-742
[3]刘久彪.基于t–copula的信用组合一致性风险度量[J].北京航空航天大学学报(社会科学版),2011,24(1):82-85.
[4]詹原瑞,韩铁,马珊珊.基于copula函数族的信用违约互换组合定价模型[J].中国管理科学,2008,16(1):1-6.
[5]童中文,何建敏.基于Copula风险中性校准的违约相关性研究[J].中国管理科学,2008,16(5):22-27.
[6]苏静,杜子平.Copula在商业银行组合信用风险度量中的应用[J].金融理论与实践,2008,346(5):6-8.
[7]彭建刚,吕志华.基于行业特性的多元系统风险因子Credit-Risk+ 模型[J].中国管理科学,2009,17(3):56-64.
[8]梁凌,彭建刚,王修华.内部评级法框架下商业银行信用风险的资本测算[J].财经理论与实践,2008,29(5):17-21.
[9]熊正德,冷梅.KMV和Apriori算法在上市公司信用风险传染中的应用[J].湖南大学学报(社会科学版),2010,24(3):58-61.
[10]Bedford T,Cooke R M.Vines-a new graphical model for dependent random variables[J].Annals of Statistics,2002,30(4):1031-1068.
[11]Aas K,Berg D.Models for construction of multivariate dependence:a comparison study[J].European Journal of Finance,2009,15(7-8):639-659.
[12]刘盛宇,杨桂元,袁宏俊.组合预测模型在我国旅游业预测中的应用[J].科学决策,2012,(3):28-42.

