弯管强化相变储热传热特性的模拟

王培伦，彭志坚，王述浩，汪 翔，丁玉龙,3

(1中国地质大学（北京）工程技术学院，北京 100083；2中国科学院过程工程研究所，北京 100190；3利兹大学颗粒科学与工程研究中心，利兹 LS2 9JT)

由于相变储热材料具有储热密度高、相变温度恒定、相变温度选择范围宽等优点，相变材料（PCM）及相变储热换热已引起国内外学者和工业界的广泛关注[1]。

相变储热材料在发生相变时与周围环境交换（吸收/释放）能量，而在此过程中，其自身温度不发生变化或变化很小。相变储热换热器是指应用相变材料进行储/释能的装置，其在室内调温、电子器件温度调节、太阳能热储存、电力“移峰填谷”、内燃机余热的回收等方面有很好的应用前景[1-7]。但是，由于相变储热换热系统的热阻较大，使其实际应用往往受到限制，因此，如何强化储热换热器的换热过程成为当前储热换热器研究的重点问题之一。

强化储热换热器的换热过程主要有增加翅片、在相变材料中添加高导热性材料等方法。Kayansayan等[8]研究了不同直径的圆形翅片以及翅片数量对储热换热系统的影响，并对其建立了数学模型，在翅片直径较小时，储能量的模拟结果与实验结果基本吻合，但在翅片直径较大时，模拟结果与实验结果差别较大；Smyth等[9]对比了轴向翅片和径向翅片对增强换热的影响，指出轴向翅片在增强换热能力上要优于径向翅片；Fok等[3]和Liu等[10]对翅片增强换热能力也进行了探索，指出增加翅片的数量能显著增强换热，而螺旋状翅片不但能增强导热，还能增强对流换热。而Fukai等[11]研究了在相变材料中加入杂乱排布和规则排布的碳纤维来增强相变材料导热性能的可能性，发现规则排布的碳纤维效果更好；在此基础上，他们还对添加均匀排布的碳纤维相变材料的导热性能进行了更深入的研究[12-13]，得出用碳纤维刷比不用碳纤维刷能显著提高导热的结论，但是由于碳纤维刷的阻力，使其在 PCM 熔化时的效果明显小于凝固时的效果，同时，碳纤维刷存在一个最优半径，当超过此半径时，导热性将不会发生显著变化；Lafdi等[14]则对填充相变材料的石墨泡沫材料储热系统进行了研究，添加石墨泡沫能显著提升材料的导热性，强化换热效果，但当石墨泡沫的孔隙率达到90%时，再减小石墨泡沫的孔隙率对强化换热的增强影响不大。Robak等[15]和Liu等[16-17]分别对储热系统中装入热管增强换热性能做了详尽的研究，对比了热管与翅片强化换热，指出热管在强化换热方面要优于翅片。其它增强相变储热系统换热性能的方法，如利用微通道、带刺铜管等也有报道[18-19]。

本工作主要对采用弯管流体通道加强换热的储热换热器进行模拟研究，这种系统尚未见文献报道。研究结果与直管通道的储热换热器进行了比较，同时分别对比研究了不同进口温度和进口速度对换热行为的影响。

1 三维熔化模型

1.1 物理模型

以左远志等[21]搭建的高温熔融盐壳管式相变换热器系统为物理模型，以便与实验结果比较。熔融盐从上端流入，经过均液板后进入相变区域的换热管路，经换热后通过下方流出。经简化后的物理模型为同心套管结构，如图1（a）所示。流体管道内部半径 r1=8 mm，管壁厚 1 mm，外部半径 r2=17 mm，管长 L=100 mm，其中弯管的曲率半径R=36.3 mm。根据文献，当外侧下端管壁温度与进口温度相当时，视为相变材料完全熔化。

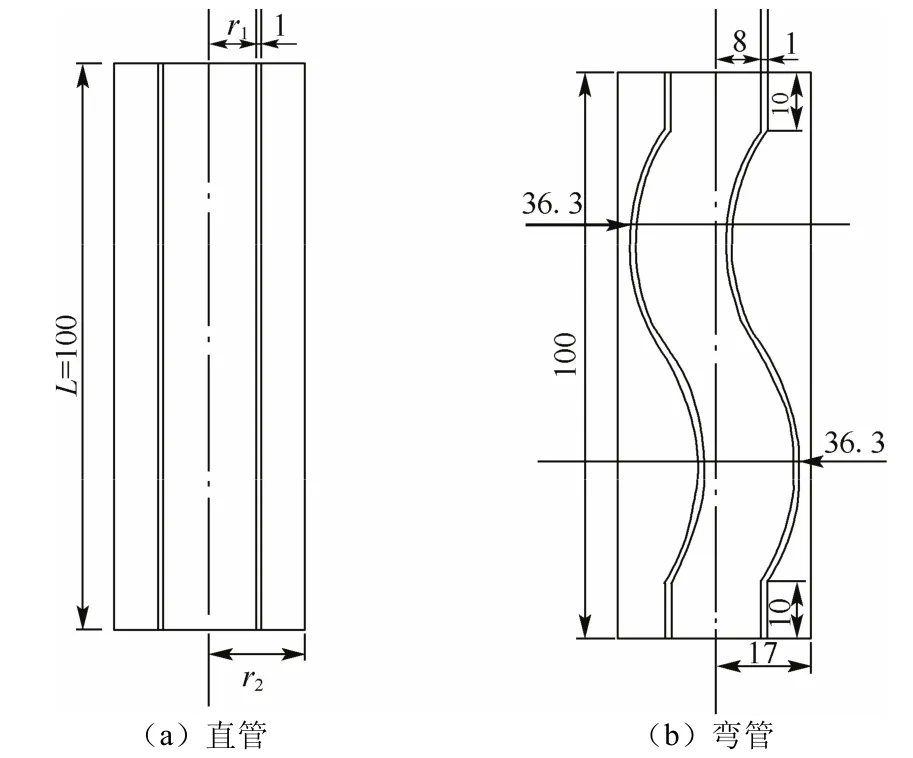
图1 直管和弯管结构模型Fig.1 The structure model of straight pipe and twisted pipe

1.2 数学模型

本文使用热焓模型，将相变区域看成多孔介质，根据孔隙率来判断材料所处的相态，其中的假设包括液相率（β）等于孔隙率。

1.2.1 PCM的控制方程

PCM区域的能量控制方程为热焓模型，将相变材料视为多孔介质，其控制方程为

连续性方程

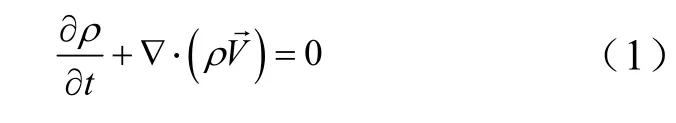
能量方程

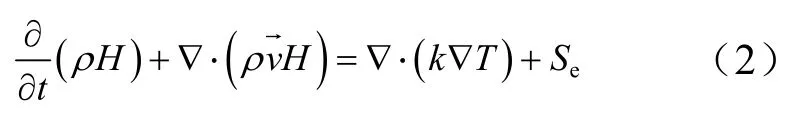
动量方程

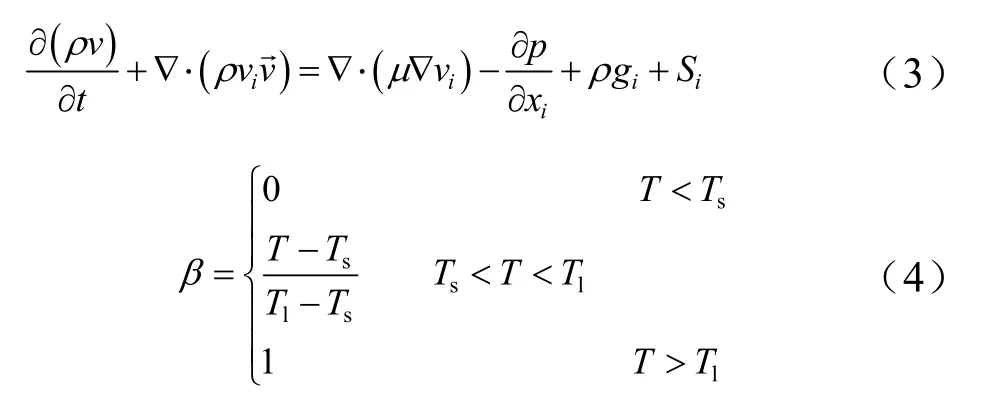
其中

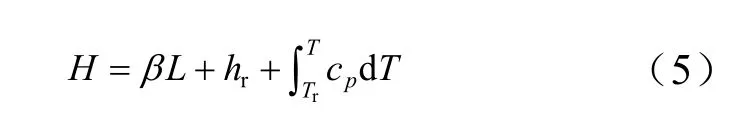
由于PCM熔化/凝固过程中的孔隙率变化，使得动量方程的源项随之变化。在模糊区动量的损失是由模糊区孔隙率的减小造成的，此源项是为了说明由于固相的存在造成的压降。模糊区动量方程的源项为

式中，ε为一个小于0.0001的数，避免分母等于0；Am为模糊区常数，为阻尼振幅尺度的量度，该值越大，则 PCM 在凝固时材料速度减到零的速度梯度越大，但该值太大会引起结果震荡；vp为随着熔化的进行固相脱离模糊区的速度，即牵连速度；Sm在i方向上的分量为Si。

湍流模型采用Realizable k-ε湍流模型，模糊区和凝固区的湍流方程（k方程和ε方程）都要加源项，用来解释凝固区孔隙率的减小，该湍流源项表达式为

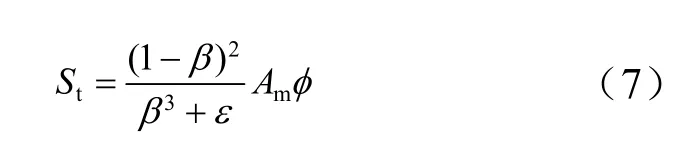
式中，φ为待求变量。

1.2.2 边界条件和初始条件

根据文献数据，采用速度进口边界条件，进口速度为0.54 m/s，进口温度为613 K；出口采用自由流出口边界条件（压力梯度为0）；外壁采用绝热壁面边界条件。直管的设置模型为非稳态、层流、固/液相变模型；弯管的设置模型为非稳态、Realizable k-ε湍流、固/液相变模型。PCM 的初始化温度为513 K。

同时对模型做如下假设：① 管口速度均匀；② 相变材料只有一个熔点；③ PCM的物性为各向同性且均匀；④ 套管两端绝热。

PCM和加热流体的物性参数见表1。

2 数值计算结果及分析

用FLUENT6.3.2软件进行模拟计算，进口设为速度进口。全部采用六面体网格，网格数为61 880个，节点数为72551个，如图2所示。

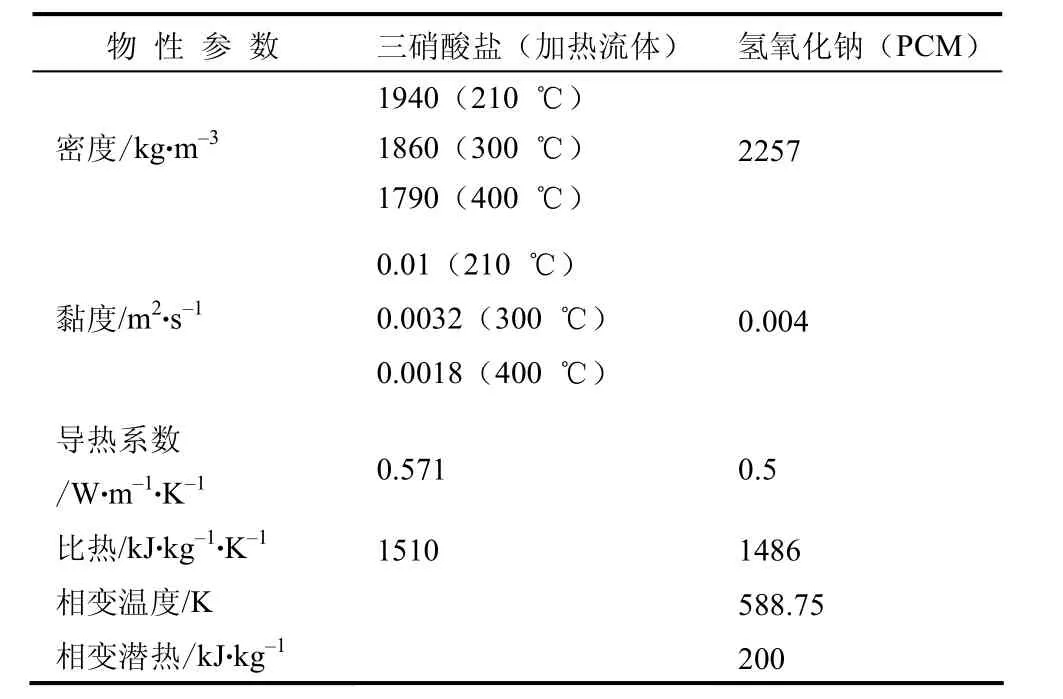
表1 PCM和加热流体的物性参数Table 1 The physical parameters of heat fluid and PCM

图2 网格图Fig.2 Grid figure

当进口流速为0.54 m/s时，对应的雷诺数Re=1236，直管内流体流动为层流。当为弯管时，由于在弯管外侧所受的黏性力大，相对于内侧的流体流动速度小，因此外侧流体所受的离心力要小于内侧流体所受的离心力，内侧流体将向外侧流动，形成二次流，因此采用带旋流修正的 k-ε湍流模型。这里的二次流就是在一定主流速度和一定几何边界条件下，黏性流体做曲线运动时所产生的一种有规律的伴随运动，常用迪恩数来表征其特性[21]，即

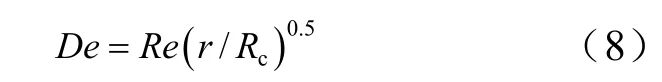
式中，Re为雷诺数；r为管径；Rc为曲率半径。如果De ＞36流体就会出现不稳定现象。当流体速度v=0.54 m/s时，De=1070＞＞36。

2.1 直管与弯管对比

图3是熔化率随时间的变化情况。可以看出，当加热流体从上端流入时，直管储热换热器 M1需要1250 s才将PCM全部熔化，而弯管储热换热器L1则只需要 1000 s左右，熔化时间比直管约缩短20%，可见弯管能显著缩短熔化时间。其原因是：首先，在L1与M2体积相同的情况下，弯管的外表面积要大于直管的外表面积，所以弯管增加了换热面积；其次，由于弯管内部流体的流动产生二次流，提高了换热系数，加快了换热进程。从图3还可看出，弯管要比直管提前熔化。图4为u=0.54 m/s、T=613 K在20 s时的熔化率云图，从图4的熔化率云图看出，弯管的熔化是从弯曲的外部开始的，这主要是因为在弯曲的地方生成了迪恩涡，二次流冲刷外壁，使弯曲外侧的换热系数高于管道的其它地方，从而使熔化从弯曲外部开始。因为熔化最先出现在中间部分而不是在顶端，所以弯管自然对流的作用要高于直管。图5为上部弯曲部分中间截面的速度矢量图，从图5可以看出加热流体在弯管处的湍流情况，在弯管处有迪恩涡出现，由于弯管的曲率小，涡流不是十分明显，但已经显著提高了换热，加快了PCM的熔化。

2.2 换热面积的对比

设计直管式储热换热器M2，令其换热面积与弯管相同。此直管储热换热器的内径r1=8 mm，壁厚为1 mm，外管径r2=16.86 mm，管长L=102.33 mm，装有与弯管相同体积的PCM。相同换热面积的直管与旁管熔化率随时间的变化对比见图6。

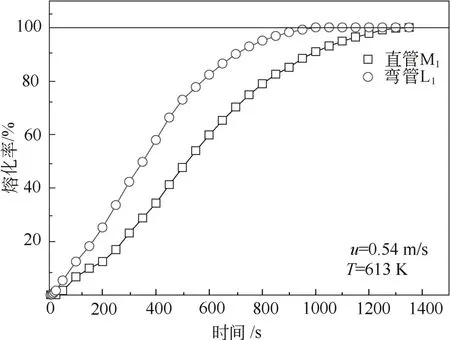
图3 熔化率随时间的变化Fig.3 The liquid fraction of PCM overtime

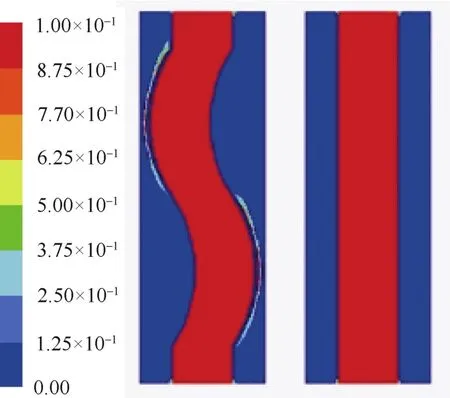
图4 熔化率云图Fig.4 The nephogram of liquid fraction

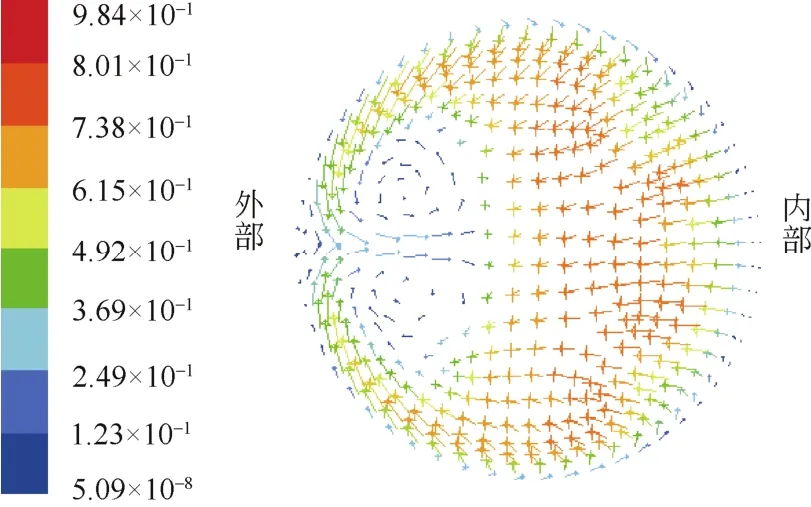
图5 加热流体的速度矢量图Fig.5 The velocity vectors graph of the heat fluid

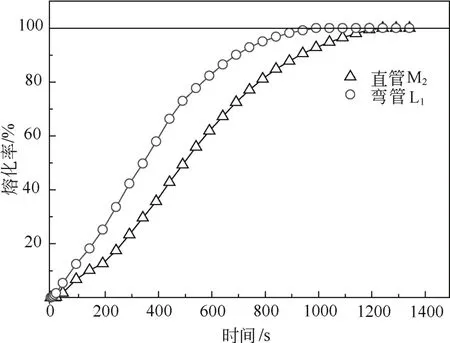
图6 相同换热面积的直管与弯管熔化率随时间变化Fig.6 The liquid fraction of straight pipe and twisted pipe with the same heat transfer surface over time

由图6可见，弯管储热换热器内部PCM全部熔化的时间比直管的熔化时间缩短150 s，熔化速率明显快于直管储热换热器。

对比两种直管储热换热器的换热时间可以看出，M2比M1的熔化时间缩短50 s，这主要是因为换热面积增加，提高了换热效率。但是通过比较换热器 M1、M2和 L1的熔化时间来看，换热器 L1性能的提高主要是因为弯管的二次流提高了换热，换热面积的增加对换热性能的影响远不及弯管二次流的影响。二次流冲刷弯管外壁，使弯管外壁处的换热加强，进而使外壁处的 PCM 先熔化。由于熔化不是从换热器的两端而是从弯曲的中间部分开始的，自然对流的影响加大，熔化时间缩短。

当进口速度为0.54 m/s时，直管的进出口压差为15.92 Pa，而弯管的进出口压差为78.89 Pa，两者相差62.97 Pa，可见弯管造成的压力损失要大不少，实际应用时应考虑这方面的影响。

2.3 进口流速对储热的影响

模拟研究了加热流体在相同的进口温度情况下，不同流动速度对储热效果的影响。图7为下端进口温度为613 K时不同流速下熔化率随时间的变化，从图7可以看出，当下端进口温度为613 K、流速大于0.54 m/s时，不同的流动速度对PCM熔化的影响不是很大，特别是当熔化比例低于90%时，加热流体流动速度对 PCM 熔化影响更小，四种速度情况下都是在500 s左右时将PCM熔化90%，之后将主要以显热储热为主。可见，在弯管储热换热器中，当流速大于0.54 m/s时，加热流体的流速不是影响换热性能的主要因素。

图7 不同流速下熔化率随时间的变化Fig.7 The liquid fraction in different velocities over time

2.4 进口温度对储热性能的影响

研究对比了在进口速度相同的情况下，不同进口温度对储热效率的影响。图8描述了在进口速度为0.54 m/s，进口温度分别为600 K、605 K和613 K三种情况下的储热性能。从模拟结果可以看出，进口温度提高对 PCM 的熔化有显著影响。在温度从600 K提高到613 K的情况下，熔化时间缩短45.8%。若以熔化90%作为潜热储热基本完成的标准来看，储热时间缩短 54.5%。进口温度的升高使换热温差增大，加快了熔化速度，并且效果要明显好于增加进口速度的方法。

2.5 弯管形状对换热的影响

图9表示了不同进口截面对熔化速率的影响。进口形状为椭圆，径比为长轴与短轴长度之比。从图9和图10的模拟结果可以看出，进口形状为椭圆的熔化效果不一定比进口为圆形的好。当径比分别为1.31、1.52和2.56时，熔化速率比圆形进口慢，熔化时间长。而当径比为1.78时，其熔化速率比圆形进口快，同时熔化时间明显缩短。可见，熔化时间与径比之间不是线性关系。这主要是因为弯管越扁平，越有利于提高换热管外扁平侧的熔化，但却不利于迪恩涡的形成，削弱了弯管外侧的换热，二者的相互作用使径比约为1.78时为最佳径比关系，此时熔化所需要的时间最短。

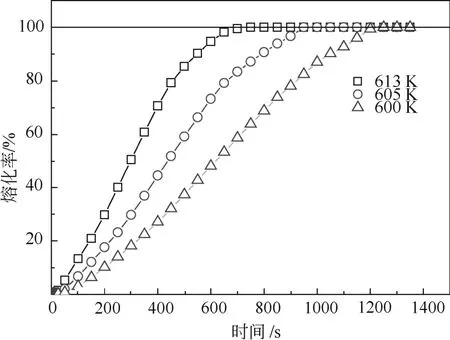
图8 进口温度对PCM熔化的影响Fig.8 The influence of inlet temperature on the melting of PCM

图9 不同形状进口截面的熔化率随时间的变化关系Fig.9 The relationship between the aspect ratio and liquid fraction of PCM over time

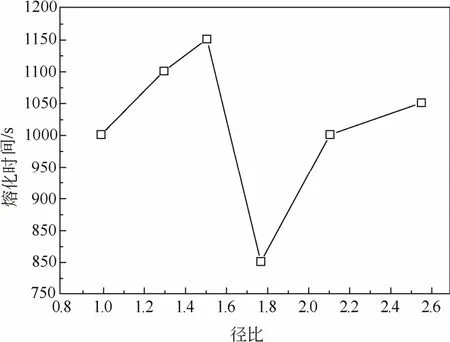
图10 径比与熔化时间的关系Fig.10 The relationship between the aspect ratio and melting time

2.6 压损分析

当弯管进口速度为0.54 m/s时，不同径比与压降的关系如图11所示。可以看出，压差随着径比的增加先减小后增加。这是因为，弯曲方向是沿短轴方向的，并且在弯管的曲率半径一定的情况下，径比越大，弯管就显得越直，由弯曲造成的阻力也就越小，因此进出口压差会减小。但是随着径比的增加，管体就会变得越薄，形状就越像平板，从而使阻力增加，进出口压差增加。

图11 不同径比对应的进出口压差Fig.11 The differential pressure with different aspect ratio

2.7 模型结果与实验结果的比较

根据文献[21]，以换热器下端外壁温度高于熔点时的时间作为储热结束的时间，模拟结果在1300 s时，下端外壁温度开始高于相变温度，而实验结果是1050 s。对比模拟结果与实验结果（图12）发现，温度变化趋势基本一致，但差别较大，其中原因有以下几点：①实际材料的物性与模拟设置的材料物性有差别；②为了与弯管情况对比，将直管模型的外壁设置为绝热边界，这与实际情况有所差别，模型还有待于改进。

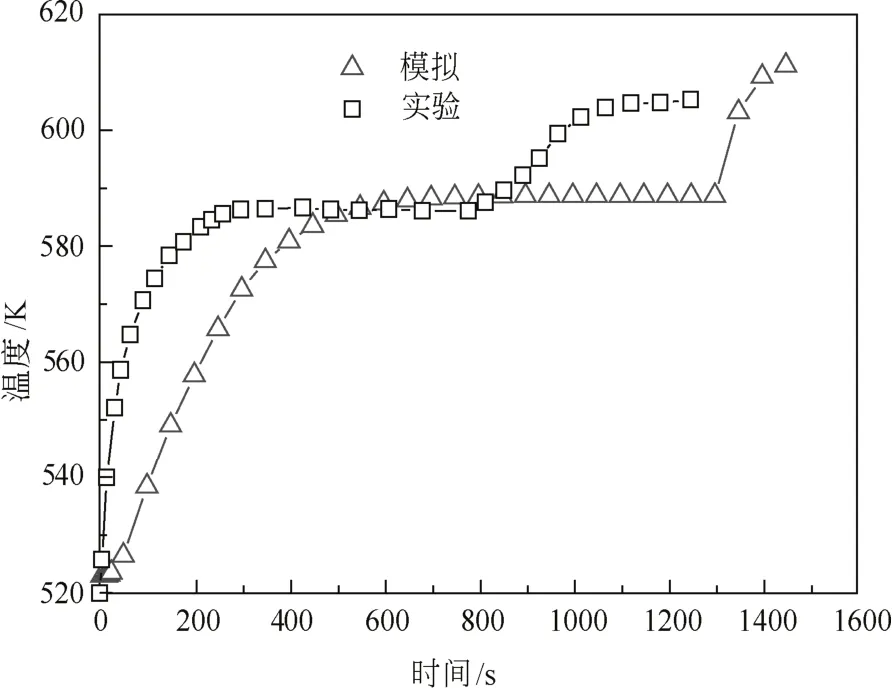
图12 实验-模拟对照Fig.12 The contract between experiment and simulation

3 结 论

（1）在相同条件下，弯管的换热效率明显高于直管的；弯管PCM的熔化不再是先出现在进口处，而是出现在弯管弯曲的中部。具有相同换热面积的直管和弯管换热器，熔化相同体积的PCM，弯管储热换热器所用的时间明显短于直管储热换热器；弯管储热换热器提高储热效率的主要原因是二次流。

（2）改变加热流体的流动方向对弯管储热换热器的储热效果几乎没有影响；只改变加热流体的流速（流量），同样对弯管储热换热器的储热效果影响不大，但加热流体的进口温度对弯管储热换热器的储热效果影响很大，随着进口温度的升高，熔化时间明显缩短。

（3）管体截面形状对储热效果有影响。随着径比的增大，熔化时间先减小后增大，在径比为1.78时熔化时间最短。

（4）弯管的弯曲造成的压力损失比直管大，在应用时，应根据实际需要选择。

[1] 张国才，除哲，陈运法，等.金属基相变材料的研究进展及应用[J].储能科学与技术，2012，1（1）：74-81.

[2] Ezan M A，Ozdogan M，Gunerhan H，et al.Energetic and exergetic analysis and assessment of a thermal energy storage(TES) unit for building applications[J].Energy and Buildings，2010，42（10）：1896-1901.

[3] Fok S C，Shen W，Tan F L.Cooling of portable hand-held electronic devices using phase change materials in finned heat sinks[J].International Journal of Thermal Sciences，2010，49（10）：109-117.

[4] Mettawee S Eman-Bellah，Assassa M R G.Experimental study of a compact PCM solar collector[J].Energy，2006，31（14）：2958-2968.

[5] Li Z F，Sumathy K.Technology development in the solar absorption air-conditioning systems[J].Renewable and Sustainable Energy Reviews，2000，4（3）：267-293.

[6] Agyenim F，Hewitt N.The development of a finned phase change material (PCM) storage system to take advantage of off-peak electricity tariff for improvement in cost of heat pump operation[J].Energy and Buildings，2010，42（9）：1552-1560.

[7] Kauranen P，Elonen T，Wikstrom L，et al.Temperature optimisation of a diesel engine using exhaust gas heat recovery and thermal energy storage（diesel engine with thermal energy storage）[J].Applied Thermal Engineering，2010，30（6）：631-638.

[8] Kayansayan N，Acar M A.Ice formation around a finned-tube heat exchanger for cold thermal energy storage[J].International Journal of Thermal Sciences，2006，45（4）：405-418.

[9] Agyenim F，Eames P，Smyth M.A comparison of heat transfer enhancement in a medium temperature thermal energy storage heat exchanger using fins[J].Solar Energy，2009，83（9）：1509-1520.

[10] Liu Zhongliang，Sun Xuan，Ma Chongfang.Experimental investigations on the characteristics of melting processes of stearic acid in an annulus and its thermal conductivity enhancement by fins[J].Energy Conversion and Management，2005，46（6）：959-969.

[11] Fukai J，Kanou M，Kodama Y，et al.Thermal conductivity enhancement of energy storage media using carbon bers[J].Energy Conversion & Management，2000，41（14）：1543-1556.

[12] Fukai J，Hamada Y，Morozumi Y，et al.Effect of carbon-fiber brushes on conductive heat transfer in phase change materials[J].International Journal of Heat and Mass Transfer，2002，45（24）：4781-4792.

[13] Fukai J，Hamada Y，Morozumi Y，et al.Improvement of thermal characteristics of latent heat thermal energy storage units using carbon-fiber brushes：experiments and modeling[J].International Journal of Heat and Mass Transfer，2003，46（23）：4513-4525.

[14] Lafdi K，Mesalhy O，Elgafy A.Graphite foams infiltrated with phase change materials as alternative materials for space and terrestrial ther mal energy storage applications[J].Carbon，2008，46（1）：159-168.

[15] Robak C W，Bergman T L，Faghri A.Enhancement of latent heat energy storage using embedded heat pipes[J].International Journal of Heat and Mass Transfer，2011，54：3476-3484.

[16] Liu Zhongliang，Wang Z Y，Ma C F.An experimental study on the heat transfer characteristics of a heat pipe heat exchanger with latent heat storage Part II：Simultaneous charging/discharging modes[J].Energy Conversion and Management，2006，47：967-991.

[17] Liu Zhongliang，Wang Zengyi，Ma Chongfang.An experimental study on heat transfer characteristics of heat pipe heat exchanger with latent heat storage Part I：Charging only and discharging only modes[J].Energy Conversion and Management，2006，47：944-966.

[18] Balikowski J R，Mollendorf J C.Performance of phase change materials in a horizontal annulus of a double-pipe heat exchanger in a water-circulating loop [J].Heat Transfer，2007，121：402-420.

[19] Sabbah R，Farid M M，Al-Hallaj S.Micro-channel heat sink with slurry of water with micro-encapsulated phase change material：3D-Numerical study[J].Applied Thermal Engineering，2008，29（2-3）：445-454.

[20] 湛含辉，朱辉，陈津端，等.90°弯管内二次流(迪恩涡)的数值模拟[J].锅炉技术，2010，41（4）：1-5.

[21] 左远志，杨晓西，丁静.高温熔融盐壳管式相变换热器的传热特性[J].华南理工大学学报，2011，39（1）：42-47.