以太网并行处理程序退避方法分析

李 隽

(北京市通州区人民检察院 技术处，北京 101100)

1 引言

以太网的发送过程中，先由一个或多个节点产生发送帧和测试线，然后尝试发送并尽快在完成当前传输。如果是多于一个节点，节点会产生碰撞，生成随机的补偿时间，然后再次尝试发送。

我们假设在以太网上均匀工作站上运行并行处理的应用程序，并考虑任务交会帧的发送。例如，在一个消息传递中，我们可能有求根程序[1]。在这里，一个已知函数在所给间隔有一个单一根，此根是程序在一次平行迭代的结果（按照所需的精确度）。在任一给定的迭代中，当前的间隔要搜索n个小区间，其中，n是机器的总数量。每一个节点检查其指定节点的子区间，然后告知上层节点给定函数在此子区间信号是否发生变化。这些子区间中只有一个会发生这样的变化，然后，它会成为新的区间。新区间端点的值将被广播，使它们可以划分成新的子区间。在共享内存范式下（分布式共享内存），屏蔽操作会产生类似的模式。

出现在这里的问题是，在许多应用中任务时间（包括通信延迟）发生小的变异[2]。例如，上述的求根过程，函数得到的时间是非常的一致的。又如，一个堆排序的r项r的平均运行时间为O相关（r log r），而标准差为O（）[3]；问题在于，相对于平均值来说，标准偏差较小。

在实际应用中，多节点任务完成的同时，任务交会的操作将导致以太网上的碰撞。随机退避的结果将减缓应用程序。在这方面，由以太网硬件所引起的随机退避通常需要更长的时间。在文献[4]中，提出编程关闭的概念来解决这个问题。假设有n个节点的任务需要处理，在节点k完成任务的时间为Tk时，运行在节点k的软件会产生自己的关闭，延迟kδ为交会帧管理器节点在发送之前的时间。通过软件产生一个小的、确定的补偿，可以避免由以太网硬件产生不必要的长补偿时间。

2 分析

令f表示每个Tk的概率密度函数，依据编程退避，确定预期的第一轮碰撞。在第一轮中，节点i和j发生碰撞，让1ij等于1，否则为0。第一轮碰撞的总数是

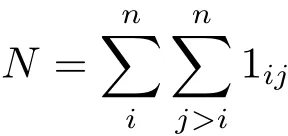
让τ表示一任务交会帧的传输时间。这通常将远远小于任务时间，因为帧通常含有非常少的数据。让Uk表示节点k的实际时间，即开始发送时间

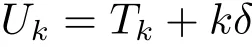
假设Uk是独立变量。那么

这里

公式(1)表明E(N)是O(n2)的幅度。适合的编程退避快速增长的系统大小为n。

公式(2)，我们可以得到一个数量的下界。

引理：假设X和Y是连续的独立的随机变量，具有相同的变化γ2和EY=EX+d。然后

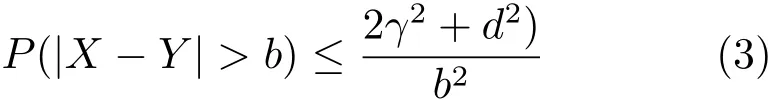
证明：首先定义Z为X−(Y−d)，从而有E[(X−Y)2]代替E[(Z−d)2]。后者的数量将等于2γ2+d2，因为Z的均值为0，方差为2γ2。然后让g表示X−Y的密度

得到的结果。

以Ui和Uj代入X和Y，

δ2是密度f的方差。

3 模拟

在预计的时间η内，所有的节点都成功发送一个消息，需要解决下列问题：

•有多少通过编程退避来改善以太网硬件管理传输？

•所有其他因素固定不变的情况下，如何设置系统n的最优值δ？

•设c为尺度参数的任务时间的密度函数，

对于一些函数h和一些恒定的Q值，由于c的增加，得到密度具有相似的形状，但更分散，并δ将正比c。

在模拟中，任务时间首先采取的是密度均匀U(1−c,1+c)。因此，周围的平均值为1.0，与c一同起到尺度参数的作用。

帧的传输时间τ，假定为小于1.0的平均任务的时间。具体地，在这里给出的所有的模拟，τ=0.1。这是一个实际的假设，否则的通信被架空（甚至无碰撞）对于有效的加速并行来说太高。

公式(2)是一个典型的关于δ的递减函数，随着δ的增加，前端会出现更多的延迟η。因此，我们可以将η看作δ的函数。

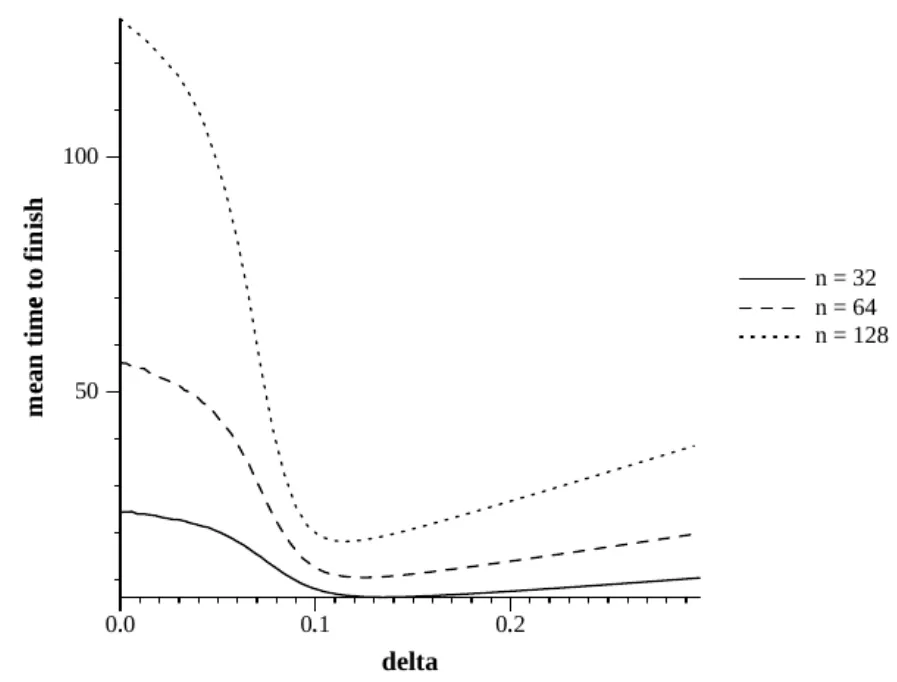
图1c=0.1

我们开始c=0.1进行一个模拟，在图1中，系统为一个较小的值，32、64和128。这里是一个在任务时间内完成的拟模拟，这就形成对我们工作的帮助。因此，编程退避具有强大的加速任务交会过程，292%、439%和619%的大小。还要注意的是，对于更大的系统，编程退避显现出更强大的作用。

作为n的函数，δ的最优值被看作是相对恒定的。近恒定查看时，在以下情况下：如果任务时间是完全不变的，δ的最优值为τ；此值将导致在一个时间表下，第(i+1)个节点开始后立即发送第i个。

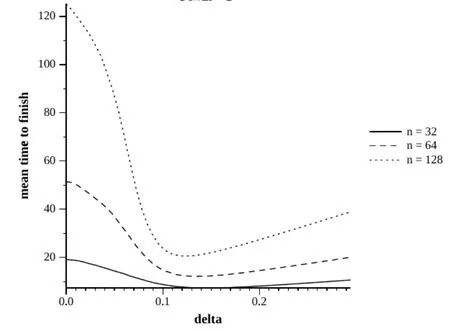
图2c=0.8

这种推理不能被应用于c=0.8的情况下，如图2所示。在任务时间变化较大的情况下，相应的加大了加速比，较为温和的条件是：158%、324%和507%。然而，有趣的是，δ的最优值与前面讨论的情况类似。

如上文所述，如果任务时间是完全恒定的，δ的最佳值为τ。因此，我们所期望的最佳的δ只是略多于设置的任务时间。进行初步模拟值τ＜0.1。此外，典型值τ是经验型的。

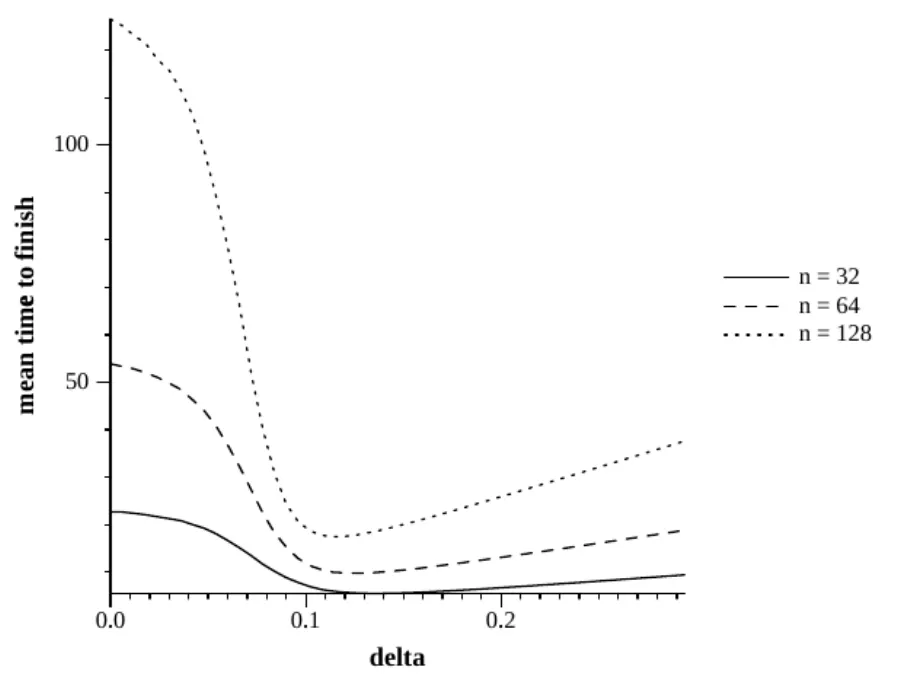
图3c=0.1分布图

图4c=0.8分布图

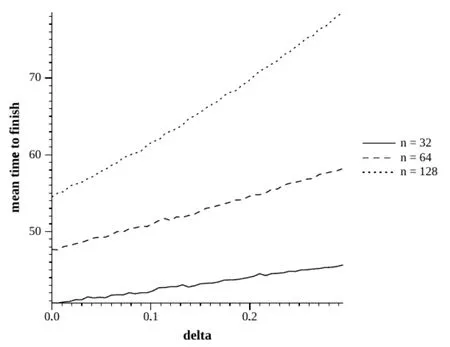
图5c=10.0分布图

然而，即使是用c=0.8的任务的时间分布具有一个相当小的标准差，所以我们转向使用指数分布，参数c是分布的平均值。图3和图4分别对应c=0.1和c=0.8。图1和图2的结果是相似的。然而，结果为c=10.0，如图5中所示，有很大的不同。这里的任务时间有足够多的变量，编程退避简单地产生多余的延迟是以太网卡所需要的。

4 讨论与结论

我们构建一个理论模型，在任务时间的小变异的影响以太网的并行处理。该模型表明，总体任务交会时间上的顺序O(n2)，我们得到一个下界的基础上的任务时间的标准偏差。

作为一个潜在的解决这个问题，我们已经发现，编程退避可以产生非常大的加速，在实际中，任务时间是一个小的标准偏差。此外，最佳值δ在这种情况下，似乎是相当不敏感的类型分布，似乎是一般约10-20%，大于一个任务交会消息的传输时间。

[1]AKL S G.The Design and Analysis of Parallel Algorithms[M].Prentice Hall,1989.

[2]ADVE V S,VERNON M K.The Inf l uence of Random Delays on Parallel Execution Times.Proceedings of the 1993 ACM Sigmetrics Conference on Measurement and Modeling of Computer Systems.1993:61-73.

[3]GONNET G.Handbook of Algorithms and Data Structures.Addison-Wesley,1984.

[4]DAVIES G,MATLOFF N.Network-Specif i c Performance Enhancements for PVM.Proceedings of the 4th IEEE International Symposium on High-Performance Distributed Computing,1995:205-210.