基于EKF的无线传感器网络移动信标定位算法

占 宏，黎善斌，胥布工

（华南理工大学自动化科学与工程学院，广东广州 510640）

无线传感器网络中节点的位置对于监测信息至关重要，没有位置信息的监测数据通常毫无意义［1］。同时，传感器网络的布局、覆盖以及目标跟踪等操作均取决于节点的有效定位。因此，节点位置的确定是无线传感器网络重要问题之一。常用的基于静态信标的定位算法需要较高的信标节点密度，增加了网络定位成本。为此，一些研究者提出了使用移动信标节点辅助未知节点的定位机制以降低成本［2］。移动信标节点在移动过程中产生众多虚拟信标点辅助定位，从而实现对未知节点更加精确的位置估计。

基于移动信标定位思想，文献［3］中Ssu等由几何学中“弦的垂直平分线通过圆心”这一性质，提出了一种非测距的移动信标辅助定位机制，但该方法需满足移动信标节点刚好通过未知节点的通信圆周，不能实现大范围的节点定位，定位效率低。Hu等在文献［4］中提出移动信标沿螺旋线轨迹运动，采用质心定位算法得到未知节点的估计位置坐标。螺旋线模型是一种简单可行的信标移动路径，但是因其无法有效地覆盖全部传感区域，易出现信标覆盖盲区，降低了定位精度。匡兴红等［5］提出一种新的分布式节点定位算法——移动锚节点极大似然算法（MAP-MLE），该算法中移动信标节点采用可调参数多、灵活性很大、网络覆盖度高的高斯-马尔可夫（Gauss-Markov）模型，但其信标节点移动路径较长，功耗大。为此，本文根据等距三重覆盖思想确定矩形传感区域中虚拟信标的位置分布，利用蚁群算法得到遍历虚拟信标的最优路径，同时引入扩展卡尔曼滤波（EKF）以提高算法定位精度。

1 移动信标定位原理

1.1 虚拟信标位置分布

虚拟信标的选择需要考虑传感区域中未知节点均可接收到3个以上不同虚拟信标数据包，以保证各节点实现定位，同时虚拟信标位置应尽可能少以减少定位时间，降低能量消耗［6-7］。

根据等距三重优化覆盖思想，当传感区域为矩形且大小为A×B，节点通信半径为r时，可得到虚拟信标发射位置坐标，步骤如下［6］。

1） 根据A和B分别计算每行中虚拟信标的数量行数imax。

2） 计算第i行和第j列虚拟信标位置横坐标xij、纵坐标yij

如计算出的坐标超出了区域（A×B）边界时，则直接用相应边界线坐标替换其坐标。

1.2 最优路径获取

获取遍历所有虚拟信标点最优路径问题可看成是典型的旅行商问题（Traveling Salesman Problem，TSP），虚拟信标点相当于TSP中的城市，确定一条经过各虚拟信标点当且仅当一次的最短路线，可采用蚁群算法来求解［8-9］。

设m为虚拟信标点数量，dij为虚拟信标点i和j的距离，τij（t）为t时刻残留在i与j连线上的信息素量。t=0时，将m只蚂蚁随机放置在n个虚拟信标点中的m个点上，设τij（0）=C（C为常数）。蚂蚁k（k=1，2，…，m） 根据各条路径上的信息素量决定转移方向。设Pkij（t）为t时刻蚂蚁k由虚拟信标点i转移到j的概率

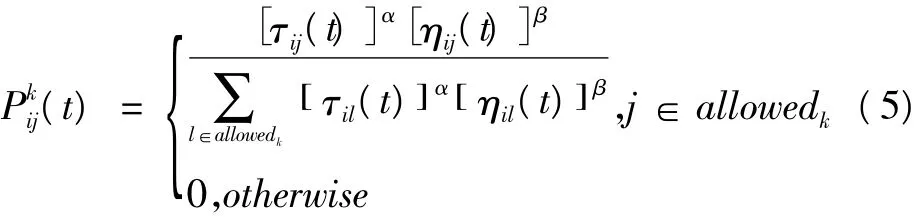
式中:ηij为启发函数，由两个虚拟信标点间的距离dij决定，表达式为

式（5）中:α和β为参数因子;allowedk是tabuk中除虚拟信标点之外的信标点，tabuk为蚂蚁k的禁忌表，记录了t时刻蚂蚁k已走过的虚拟信标点，防止其在本次循环中再次访问这些信标点，循环结束时禁忌表将被清空。τij（t+n）为t+n时刻蚂蚁残留在路径（i，j）上的信息素量;Δτij（t）为信息素量增量;（1－ρ）为信息素轨迹残留因子，为避免路径上信息素量的无限累积，通常设ρ＜1。蚂蚁完成一次循环，各路径上的信息素量根据以下两式进行调整

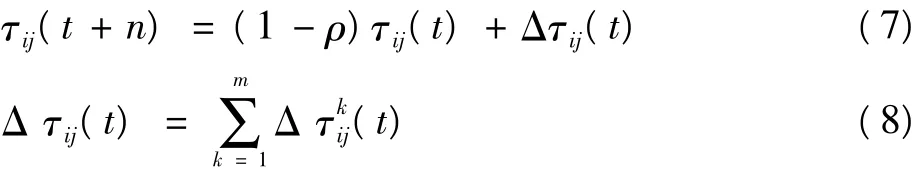
式中，Δ的计算采取Ant cycle system模型

1.3 扩展卡尔曼滤波模型

1.3.1 状态方程模型

式中:Xk=［xkyk］T为未知节点在第k－1个信标位置进行滤波后的坐标向量。wk是测量过程噪声，A为二阶单位矩阵。

1.3.2 观察方程模型

文中采用未知节点接收到移动信标信号时的RSSI值作为EKF的观察量。观察方程为

式中:

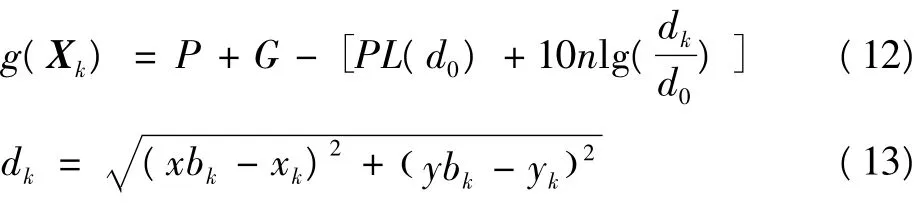
H为g（Xk）的Jacobian矩阵，即

式中:dk为未知节点到第k个虚拟信标的距离，P为发射功率，G为天线接收增益，n为路径衰减因子，范围为2～5，（xbk，ybk）为未知节点收到第k个信标的坐标，vk为观察噪声，根据文献［10］设σ1为4～10。

根据状态方程和观察方程，得EKF计算过程［11］。

1）利用系统上一状态预测现在的状态

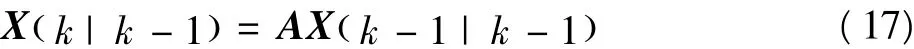
2）更新系统现在状态的协方差矩阵

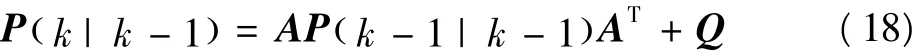
3）计算EKF增益

4）结合预测值和观察值，估计现在状态的最优估计值

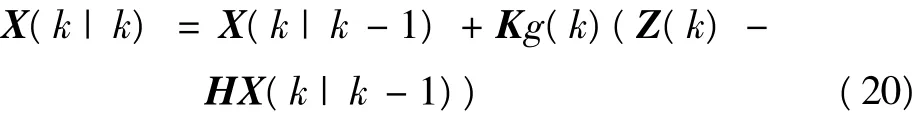
5）更新现在最优估计值的协方差

6）循环迭代，返回步骤1。

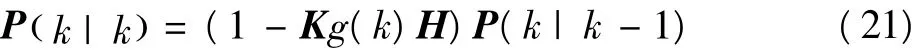
式中:Q为过程噪声协方差矩阵，Q=0，R=为观察噪声协方差矩阵，σ1为高斯分布vk的标准差。

2 算法设计

根据上述移动信标辅助定位机制，本文算法具体步骤如下。

1）由式（1）（2）确定传感器区域（A×B）虚拟信标位置的分布;

2）采用蚁群算法得到最优遍历路径;

3）移动信标按照最优路径遍历传感区域，并在虚拟信标点发送定位数据包;

4）未知节点接收信标信息，并只存储RSSI值最高的前 s个信标点位置信息，［（xi，yi）;RSSIi］;

5）未知节点对收到的信标节点信号依其RSSI值从大到小排序，并建立以下3个集合:

（1） 信标点RSSI集合，Beacon_set={RSSI1，RSSI2，…，RSSIs}，RSSI1≥RSSI2≥…≥RSSIs;

（2）未知节点与各信标点的距离集合，Distance_set={d1，d2，…，ds};

（3）信标点位置坐标集合:Position_set={（xb1，yb1），（xb2，yb2），…，（xbs，ybs）}。

6）采用加权质心算法得到未知节点的近似估计坐标（xest，yest） ，即

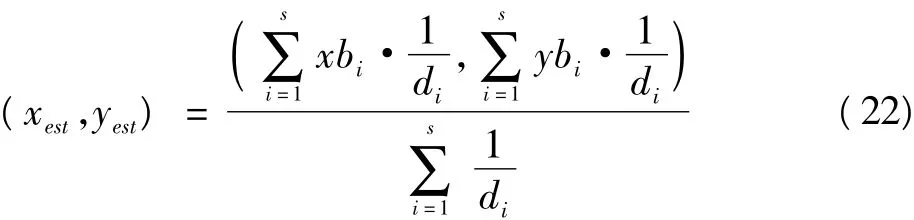
7）将该近似估计坐标作为EKF的初始状态，采用EKF得出未知节点的精确估计坐标。

3 仿真结果与分析

3.1 虚拟信标分布及最优路径

设传感器区域S（50 m×50 m），节点通信半径为r=10 m时，由1.1中的方法得到42个虚拟信标点。采用蚁群算法得到移动信标最优遍历路径如图1所示，路径总长度为391.25 m。

本文对不同的节点通信半径所对应的虚拟信标节点数目和遍历路径长度进行了比较，结果如表1所示。从该表中可以得出，节点通信半径越大，虚拟信标点的数目越少，遍历路径越长。

图1 移动信标最优遍历路径图

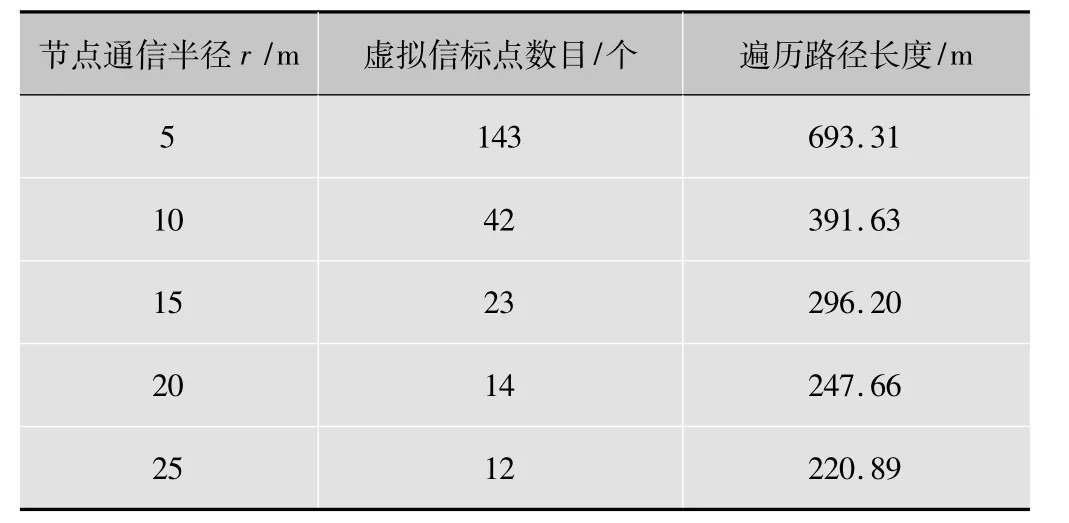
表1 虚拟信标点和遍历路径长度比较

3.2 定位误差分析

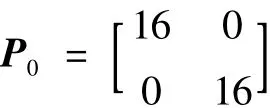
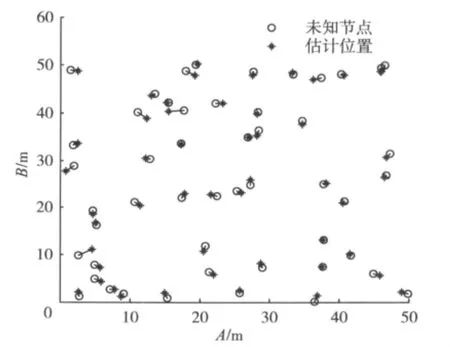
图2 定位结果示意图

图3是传感器节点通信半径取不同值时，加入EKF后的算法与普通加权质心定位算法的平均定位误差比较。从图中可以看出，对于相同的节点通信半径，本文算法的定位误差明显小于加权质心算法的误差;由于节点通信半径越小，虚拟信标点越多，即信标节点密度高，因此其定位误差越小。

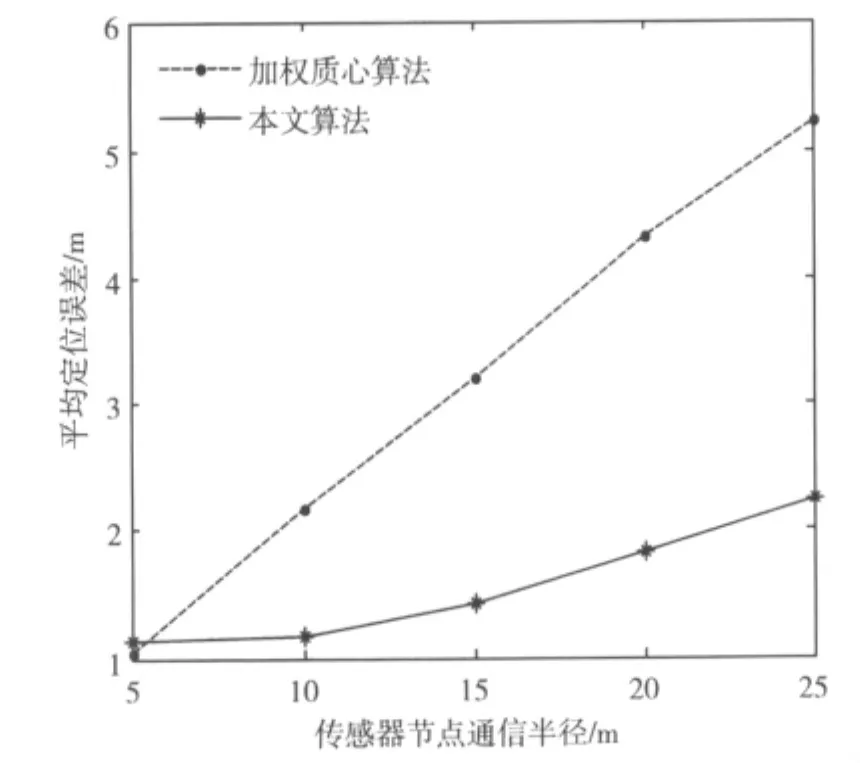
图3 不同通信半径时的定位误差比较

由于EKF的精度与迭代次数有关，本文通过仿真得出了s的取值对算法定位精度的影响，结果如图4所示。由图可知，加权质心算法由于不能消除测量RSSI值误差的影响，其定位误差随s的增大而增大。而迭代次数s的取值越大，本文算法的平均定位误差越小，当s=7时，定位误差最小为1.04 m;当s＞7时，定位误差由于受测量RSSI值的影响，误差增大。

图4 迭代次数与平均定位误差的比较

4 小结

本文采用等距三重覆盖思想得出矩形传感区域的虚拟信标点的位置分布，提高了网络覆盖度，利用蚁群算法获取移动信标最优遍历路径，降低了网络成本及功耗，同时采用扩展卡尔曼滤波方法提高了定位精度。当迭代7次时，其定位误差最小为1.04 m。

由于移动信标节点的路径规划是保证定位效果和效率的关键所在，因此基于本文下一步的研究主要是确定更优的移动信标运动模型，同时降低算法复杂度。

：

［1］章浩，李萍萍，张西良.无线传感器网络节点定位机制研究［J］.电视技术，2006，30（10）:71-73.

［2］SUN GuoLin，GUO Wei.Comparison of distributed localization algorithms for sensor network with a mobile beacon，in Networking［C］//Proc.2004 IEEE International Conference on Sensing and Control.［S.l.］:IEEE Press，2004:536-540.

［3］SSU K F，OU C H，JIAU H C.Localization with mobile anchor points in wireless sensor networks［J］.IEEE Transactions on Vehicular Technology，2005，54（3）:1187-1197.

［4］HU Zhen，GU Dongbing，SONG Zhengxun，et al.Localization in wireless sensor networks using a mobile anchor node［C］//Proc.IEEE/ASME International Conference on Advanced Intelligent Mechatronics.［S.l.］:IEEE Press ，2008:602-607.

［5］匡兴红，邵惠鹤.一种新的无线传感器网络节点定位算法研究［J］.传感技术学报，2008，21（1）:174-177.

［6］李石坚，徐从富，杨旸，等.面向传感器节点定位的移动信标路径获取［J］.软件学报，2008，19（2）:455-467.

［7］SICHITIU M L，RAMADURAI V.Localization of wireless sensor networks with a mobile beacon［C］//Proc.2004 IEEE International Conference on Mobile Ad-hoc and Sensor Systems.［S.l.］:IEEE Press，2004:174-183.

［8］徐云剑，彭沛夫，郭艾寅，等.基于蚁群算法的WSN移动信标路径获取研究［J］.计算机工程与应用，2008，44（28）:113-116.

［9］QIN F，CHEN W，LIU K Z，et al.，Study on mobile beacon trajectory for node localization in wireless sensor networks［C］//Proc.2010 IEEE International Conference on Information and Automation.Harbin，China:IEEE Press，2010:1577-1581.

［10］陈维克，李文锋，首珩，等.基于卡尔曼滤波的WSNs节点定位研究［J］. 武汉理工大学学报，2007，29（8）:112-116.

［11］付梦印，邓志红，张继伟.Kalman滤波理论及其在导航系统中的应用［M］.北京:科学出版社，2003.

［12］RAPPAPORT T S，RAPPAPORT T.Wireless communications:Principles and practice［M］.2nd Ed.New Jersey:Prentice Hall PTR，2002.