基于压缩感知的信号检测方法

黄继海，张晓红，罗文宇

（1.中州大学信息工程学院，河南郑州450044;2.国家数字交换系统工程技术中心，河南郑州 450002）

压缩感知理论使得稀疏信号可以在低于Nyquest采样定律的情况下进行“模拟——信息转换（AIC）”，这实际上就是针对连续时间信号的压缩感知。文献［1-2］设计出的AIC结构以压缩感知理论为基础，在模拟端对信号进行随机测量处理，这样可以远低于Nyquist速率进行采样。然而这种结构要求已知先验信息或者对噪声水平的估计以设计算法参数和算法停止条件。针对这一问题，文献［3］提出一种不需要已知噪声信息的方法，即联合凸优化方法。其主要思想是将噪声和观测误差最小化作为优化目标，在Nyquist采样速率的一半情况下，原始信号信息可以在-10 dB信噪比情况下得以精确重构。

压缩感知提出几年来，针对它的研究主要集中在如何精确重构原始信号上，然而某些应用场合并不需要完全精确重构原始信号，比如通信信号。文献［4］分析了压缩检测问题。并提供了估计的理论界和经验结果。文献［5］出了一种子空间压缩检测方法。它利用线性信号模型为在相同子空间的信号提供一种通用的解调方案。文献［6］结合传统的视频编解码技术，提出了一种基于压缩感知的视频编解码器。文献［7］也提出了一种基于压缩感知的UWB回波信号检测方法。然而以上文献的研究仅仅是对压缩采样后信号的检测问题，并没有考虑信道估计对接收性能的影响，也没有针对压缩采样对Rake合并的影响进行研究。

本文针对以上问题，力图通过完整的理论推导，分析基于压缩感知的信号检测问题，确定最优的检测方案。首先将需要高采样频率复杂信道估计［7］转化为压缩感知非完全信号重构问题，大大降低了信道估计的复杂度。其次，在压缩感知框架下，将Rake合并在压缩域完成，提出一种压缩相关器，避免模拟域实现Rake合并时由于模拟延时线不精确带来的误差。最后，通过仿真及性能分析验证了本文提出的检测方法。

1 基于压缩感知的信号检测

压缩感知理论是一种新的在采样的同时实现压缩目的的理论框架［8］。它与传统的Nyquest采样定理不同。压缩感知之所以能够用于信号、图像和其他数据的处理，是因为Nyquest信号表示仅仅利用了信号的最小先验信息——带宽，然而感兴趣的许多信号是结构化的，而且依靠比带宽更小的自由度，在可压缩信号中有用信息的内容能够直接压缩为少量数据。

根据文献［1-4］可以得到一种大大减少采样频率的基于压缩采样技术的模数转换器，其结构如图1所示，这种结构的采样频率选取不需要考虑信号带宽，只和信号稀疏度有关。

图1 无线通信系统压缩采集结构

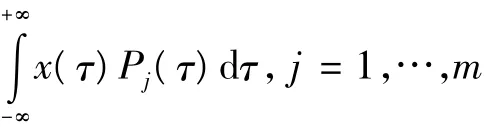
式中:Pj（t）为连续函数，j=1，…，m。

基于CS的数据重构仍然有很多不足，例如完美重构需要的过观测因子比较大，c≈lb（1+N/K）;重构算法大都需要很高的计算复杂度等。因此近年来有文献研究对压缩后的信号进行压缩检测。然而这些文献研究的仅仅是对压缩采样后的信号进行最大似然检测，没有考虑压缩后的数据对信道估计和各种分集等技术的影响。下面基于压缩感知理论，对图1采集后的信号在压缩域进行检测。首先利用压缩采样得到的导频信号估计出系统所需要的多径数及其幅度、时延值。利用正交匹配跟踪算法，对压缩采样的导频信号进行重建，其中冗余原子库可以由发送的成型脉冲及其延迟构建。由于进行了压缩处理，接收的信号的多径幅度和时延都会改变，传统Rake合并方式不再有效。因此本文利用前面估计的信道信息对接收的压缩采样信号进行压缩域的Rake合并。最后经过压缩最大比合并后的数据进行压缩判决得到发送信号的检测结果。其结构如图2所示。

1.1 压缩信道估计

本文设计一种非完全重构信道估计算法，算法流程如下。

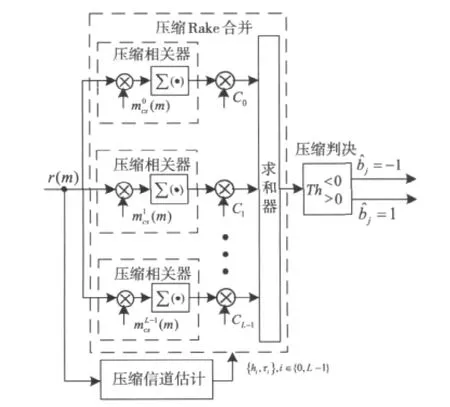
图2 压缩信号检测结构框图

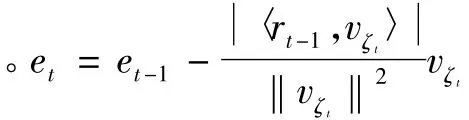
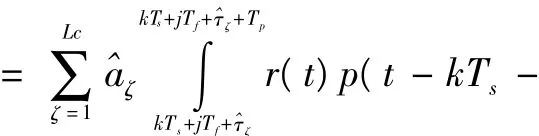
第5步，误差统计。将判决后的b（k）还原成Nf个发送脉冲与训练序列b（k）对应的Nf个脉冲，求其最小均方误差。其目的是提高非完全重构因子以增加信道估计精度。如果不为零，转第2步。否者J=J+1，如果J=n结束，否者回第2步，其中n的值随信噪比的变换而设定，非完全重构因子α定义为迭代次数与信道可分辨经的比值。

信号检测系统并不需要对信号的精确重构，只需要估计大多数比较大的多径，在系统性能和复杂度之间折中。通过将判决后的数据引入CS信道估计中作为下一次迭代的先验信息，降低了迭代次数和导频数量。

1.2 压缩Rake合并

文献［9］根据提出的压缩信道估计结果进行Rake合并，但是它的相关和合并过程在模拟域完成。由于模拟延迟线精度不高等原因，这样做的误码率性能不高。下面针对压缩采样对Rake合并的影响进行研究。因为压缩采样在基带前端进行，Rake接收机的输入是经过压缩的数据，很显然信号的延迟和幅度信息都改变了，传统的Rake接收方式并不适合处理压缩信号。下面进行压缩Rake接收机的推导。

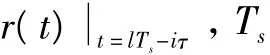
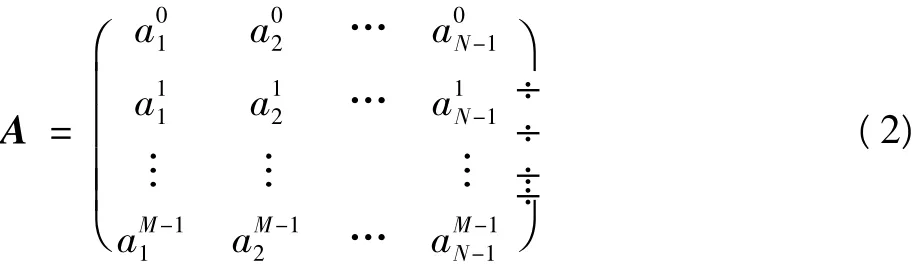
首先考虑如果Rake合并在模拟域完成，则

用以Ts为采样频率表示为

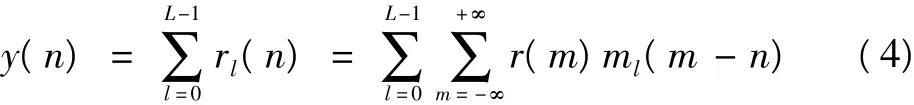
为分析方便，只考虑第一条径，写成矩阵形式

式中:M为模板m（i），i∈{0，N－1}的toeplitz矩阵形式

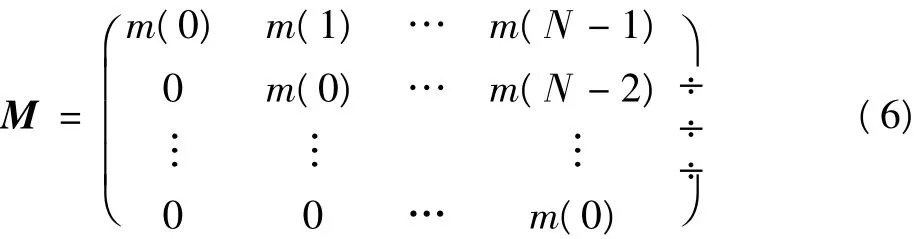
为了进行信号检测，需要判断Th=R，是一个N×1维的矢量。如果Th＞0，则bj的估计值=1;如果Th＜

下面分析Rake合并在压缩域完成，压缩模板设为mcs（i），i∈{0，M －1}，则压缩合并后的信号为

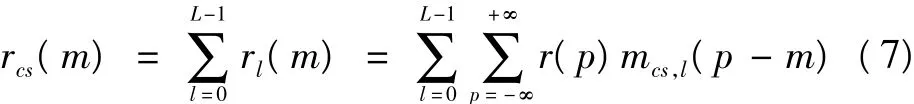
只考虑第一径得

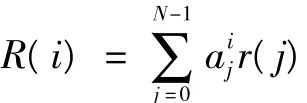
令两式子相等，则可得

可以求出压缩模板矩阵为

其中AH为观测矩阵A的共轭转置。

虽然压缩采样可以用少部分随机测量提供可以用于近似完全重构的信息，但是如果不进行重构，压缩测量则不能收集足够的信号能量，很难进行检测。文献［5-10］根据Nyquist采样条件下的信号检测，推导出压缩采样条件下的信号检测。并没有考虑Rake合并的影响，本文将Rake合并后的信号进行压缩检测，由于压缩相关增强接收信号的信噪比，因此其抗干扰能力更强。具体分析如下:压缩合并后Rake接收机输出信号可以表示为

式中:M'=（c0M0+c1M1+ … +cL－1ML－1） ，为最大比合并框架下的各个支路模板矩阵的和，ci，i∈{0，…，L－1}是由最大比合并策略确定的系数。可得判断量表示如下

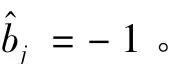
2 仿真及性能分析

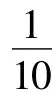
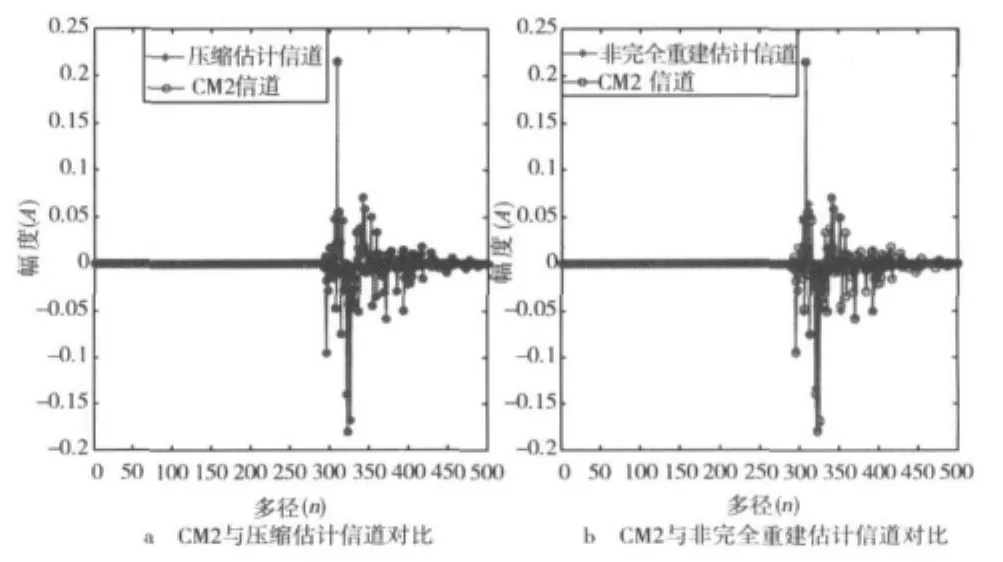
图3 压缩信道估计和非完全重构信道估计与CM2信道对比

图4为非完全重构因子α与系统误码率的关系。可以看出当α≥0.25时，信号的误码率性能逼近α=1即信道被完全估计出来的情况，而此时信道估计的复杂度比α=1时大大降低。信噪比越高，小的非完全重建因子条件下的判决误码率就越低。非完全重构压缩信道估计之所以能降低接收机实现复杂度是因为它可以降低信道估计时的迭代次数，在保证系统性能的基础上进行动态调整估计出的信道数量。

图4 非完全重构因子α在不同信噪比条件下的性能

图5为本文提出的压缩判决方法以及传统基于压缩感知的判决方法和以Nyquist速率采样条件下判决方法的误码率性能对比。

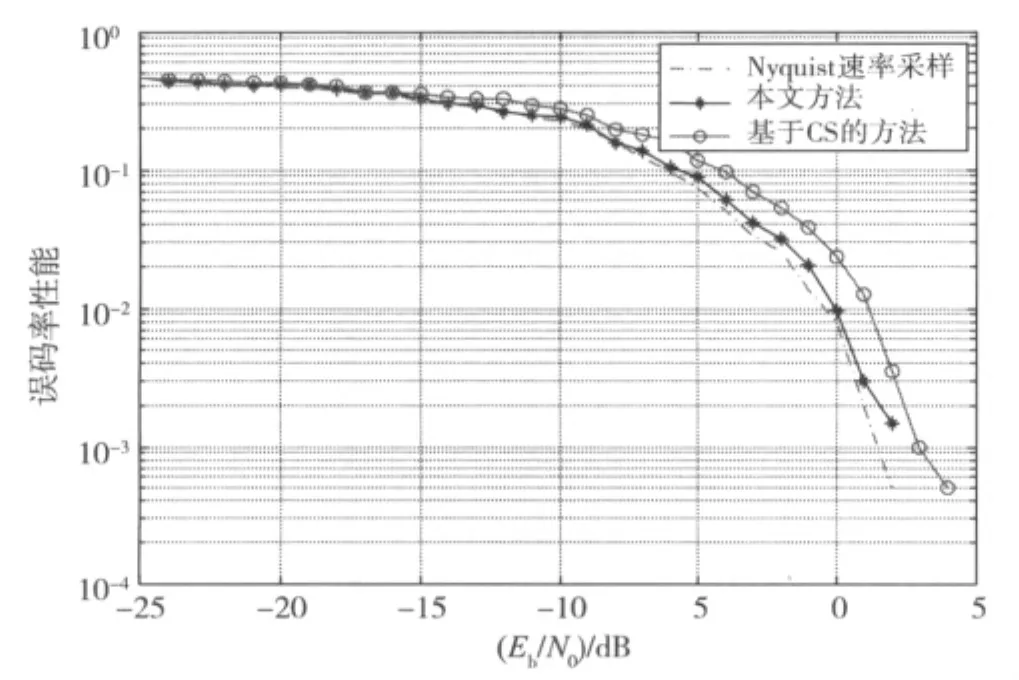
图5 各种判决条件下的误码率性能对比

由图5可知，传统基于压缩感知的判决方法性能比基于Nyquist速率采样条件下的判决方法性能差［10］，这主要是因为这种判决方法利用压缩后的数据，采集到的能量较弱，所以抗干扰能力差。虽然本文所提方法也是利用压缩后的数据，但是本文方法首先利用压缩相关器将信号的能量集中，然后再进行压缩检测，提高了接收机抗干扰性能，因此比传统压缩检测方法性能更好。由误码率曲线可以看出本文压缩检测方法与基于Nyquist速率采样条件下判决方法性能相差不大，但处理的数据量却大大降低。

3 小结

本文研究了基于压缩感知的信号检测问题。首先将信道估计转化为复杂度更低的非完全信号重构过程;然后借鉴普通Rake接收思想推导出压缩域进行相关的方法，并结合信道估计得到的最小多径参数进行最大比合并;最后将合并后的信号进行压缩判决。因为处理的是经过压缩的采样数据，数据数据只有Nyquist速率的10% ，该检测方法大大降低信道估计和多径合并的复杂度。

：

［1］KIROLOS S，LASKA J，WAKIN M，et al.Analog-to-information conversion via random demodulation［C］//Proc.IEEE Dallas/CAS Workshop on Design，Applications，Integration and Software.Richardson，TX:IEEE Press，2006:71-74.

［2］YU Z，HOYOS S，SADLER B M.Mixed signal parallel compressed sensing and reception forcognitive radio［C］//Proc.IEEE International Conference on Acoustics，Speech，and Signal Processing.Las Vegas，Nevada，USA:IEEE Press，2008:3861-3864.

［3］ZHANG Zhenghao，PEI Changxing，CHEN Nan，et al.Robust reconstruction under unknown SNR signal for analog-to-information conversion［C］//Proc.IEEE International Conference on Industrial Electronics and Applications.Xi'an，China:IEEE Press，2009:576-579.

［4］DAVENPORT M A，WAKIN M B，BARANIUK R G.Detection and estimation with compressive measurements［EB/OL］.［2011-05-07］.http://www-stat.stanford.edu/～markad/publications/dwb-tr-2006.pdf.

［5］WANG Zhongmin，ARCE G R，SADLER B M.Subspace compressive detection for sparse signals［C］//Proc.IEEE International Conference on Acoustics，Speech and Signal Processing.［S.l.］:IEEE Press，2008:3873-3876.

［6］谢晓春，赖昭胜，杨汉祥.基于压缩感知理论的视频编解码器［J］.电视技术，2010，34，（5）:21-24.

［7］PAREDES J L，ARCE G R，WANG Zhongmin.Ultra-wideband compressed sensing:channel estimation，selected topics in signal processing［J］.IEEE Journal of selected topics in Signal Processing，2007，1（3）:383-395.

［8］石光明，刘丹华，高大化，等.压缩感知理论及其研究进展［J］.电子学报，2009，37（5）:1070-1081.

［9］CANDèS E J，WAKIN M B.People hearing without listening:an introduction to compressive sampling［J］.IEEE Signal Processing Magazine ，2008，25（2）:1-13.

［10］张聪，申敏.基于OFDM-UWB系统信道估计方法的研究［J］.电视技术，2008，32（7）:64-66.