多元统计分析方法在钛白粉生产水解工序能力评价中的应用研究

任小青

(攀枝花出入境检验检疫局 四川攀枝花 617000)

1 前言

目前，国家质检总局颁布的113号令《出口工业产品企业分类管理办法》已在各地检验检疫机构广泛实施，新办法突出体现了对出口工业品由重检验向重生产过程尤其是关键工序监管转移的科学理念。四川检验检疫局推出了出口工业产品“1+1+X”(即风险评估+分类管理+关键点监管)分类管理模式，提出了运用工序能力指数对出口工业品的关键生产过程实施有效监管的措施。笔者通过对出口钛白粉企业监管的实践，进行了钛白粉生产中水解工序能力指数评价方法的有益探索。目前我国绝大多数钛白粉生产是采取硫酸法工艺，而水解工序是硫酸法生产钛白粉工艺非常重要的关键过程。工序质量决定输出的产品质量，输出产品质量反映工序能力大小。通常评价工序能力直接采用传统的一元工序能力指数Cp和Cpk进行评价;由于水解工序输出的质量特性指标不是单一的，且质量指标之间具有一定的相关性，因此无法直接进行科学评价［1］。本文将多元统计分析方法首次应用到钛白粉生产的水解工序能力指数Cp和Cpk的计算，较好地解决了这一问题。

2 水解工序的质量指标

硫酸法钛白粉生产过程中水解工序的主要产物是偏钛酸(H2TiO3)沉淀浆料，一般对偏钛酸质量的要求是水解沉淀量大(企业收率高)、沉淀粒子大小和分布适宜(钛白粉颜料性能好)以及沉淀浆料的过滤效果良好(有利于下一道水洗工序操作)等三个方面，并且三个方面相互存在着一定的相关

性，生产企业常通过监控水解率、沉降速度、D50(也有采用D43或D32等)、抽滤速度等指标判断上述三个方面是否达到要求，其中水解率反映水解的程度，沉降速度和D50均反映水解沉淀粒子的大小与分布，抽率速度反映水解浆料的过滤效果［2］。由于一般企业D50质量指标是采用激光粒度分析仪检测，与沉降速度方法相比，检测精度高，测量波动小。因此，本文选择水解率、D50、抽滤速度三项质量指标来考察水解工序能力。

3 方法原理

3.1 工序能力指数计算与判定方法

3.1.1 潜在工序能力指数Cp和实际工序能力指数Cpk

当工序输出的均值μ与容差中心M=(USL+LSL)/2重合，潜在工序能力指数 Cp=(USLLSL)/6σ，式中USL是质量特性的规范上限，LSL是质量特性的规范下限，σ是工序输出的标准差。

当工序输出的均值μ与容差中心不相重合时，实际工序能力指数Cpk=(1－K)Cp，其中K=2|M－μ|/T，T=(USL－LSL)，或 Cpk=min{(USL－μ)/3σ，(μ －LSL)/3σ}。

3.1.2 工序能力指数判定方法

应用Cp和Cpk对工序能力状况进行判定的一般方法［3，4］见表 1。

表1中，当工序输出的均值与容差中心重合时，按Cp值进行工序能力状况判定;当工序输出有漂移时，且Cp≥0.67时，按Cpk值进行工序能力状况判定，而当Cp＜0.67时，由于生产漂移带来的偏移量不可忽视，Cpk不能真实判定实际工序能力状态，可直接认定此时工序能力状况处于严重不足的区域。

3.2 多元统计分析的基本方法

在生产工序处于稳态下抽取一定质量数据样本(样本数＞30)，分别运用Grubbs准则检验异常值、Shapiro－Wilk法检验正态性以及Pearson法检验相关性，并将数据进行无量纲化(Z标准化)处理，组成矩阵X=(xij)m×n，其中m表示质量指标，n表示样本数。

运用主成分分析法求解因子模型方程［5］:X=LF+ε，其中F是按照主成分分析法选择的r个属于矩阵X的公共因子矩阵(r×1)，L是因子载荷矩阵(m×r)，ε是属于矩阵X的特殊因子矩阵(m×1)。利用矩阵X的协方差矩阵S=(Sij)m×m(其中Sij是原变量xi与xj的协方差，当i=j时，Sii是xi的标准差)经过一系列的正交标准化矩阵变换，得到矩阵S的特征值 λi和特征向量 Ei(i=1，2，...，m)，从而求得因子载荷矩阵

由于矩阵L中的第j列元素与主成分分析中第j个主成分因子Fj=∑mi=1aijxi'的系数 aij相差 λj倍，aij=lij/λj，lij为矩阵L的元素。按照上述方法进行各主成分因子Fj规范上下限转换。

根据特征值或因子方差的累计贡献率≥0.85原则，提取var(F)较大的主成分因子构成F(F1，F2，...，Fr)，r≤m;根据应用权重 ωj方法［6］，计算提取的各主成分因子权重系数为:

MCp=ΣωjCpFj，MCpk=ΣωjCpkFj;其中 j=1，2，...r，CpFj和 CpkFj为已提取的主成分因子 Fj所对应的工序能力指数值。

4 实例应用

在某钛白粉出口企业生产线的水解工序上连续抽取处于工艺稳态的偏钛酸样本50个，分别进行水解率、抽滤速度、D50等三项质量指标的检测，得到三组各50个原始质量指标数据(原始数据省略)，按照上述方法原理进行统计处理和分析。

4.1 原始质量数据的统计处理

将水解率、抽滤速度以及D50等三组数据分别进行Grubbs检验、Shapiro－Wilk检验以及三组数据的Pearson相关性检验，检验结果表明:(1)没有检出异常值，所有质量指标数据都应该保留;(2)三组数据均具有正态分布;(3)三组数据中水解率与抽滤速度两指标在置信度为0.01水平上有显著性相关。

4.2 应用多元统计方法分析计算

把原始质量数据列排成3×50的矩阵X，其中数据做无量纲标准化处理，算出矩阵X的协方差S，对其进行标准正交化处理，得到相应矩阵的特征分析结果(表2、表3):

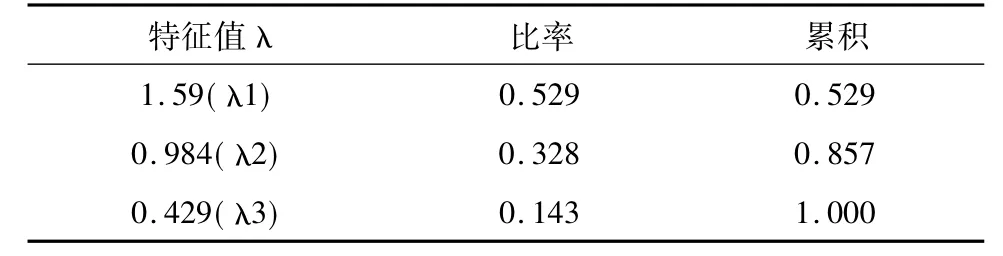
表2 特征值λ分析

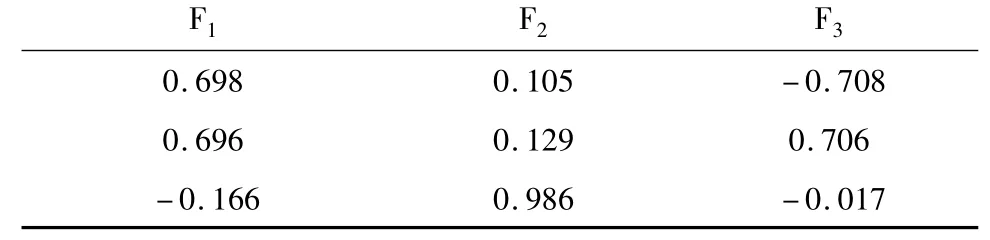
表3 主成分F系数表

由表2可知，λ1、λ2对应的主成分F1和F2所提供的信息量(方差)占原始质量指标数据总信息量(总方差)比率的总累积率大于85%，故从表3中提取主成分F1和F2表述原始质量指标的信息:F1=0.698X1+0.696X2－0.166X3和 F2=0.105X1+0.129X2－0.986X3;

将水解率、抽滤速度以及D50等原始质量指标数据规定的上下限投射到新变量空间，可以得到主成分规定范围上下限为 F1(－1.852，5.544) ，F1( －3.541，4.161);并且经 Shapiro－Wilk 正态性检验表明，F1、F2均服从正态分布，即 F1－N(0，1.2592)，F2－ N(0，1.0232)。分别计算 F1、F2工序能力指数为:

F1:Cp=1.579，Cpk=0.799;F2:Cp=1.568，Cpk=1.450

由 ω1=0.6177，ω2=0.3823 计算出水解工序综合能力指数为 MCp=1.57和MCpk=1.04。

5 结果与讨论

(1)由于四川检验检疫局将工业品出口企业分为四个管理类别(国家质检总局出台的出口工业品企业新分类管理办法中也将出口工业品企业监管类别分为四类)，并与工序能力指数Cp(或Cpk)的等级相对应(见表1)，故利用工序能力指数等级判定工序能力状况的方法为出入境检验检疫机构开展关键工序分类监管提供了科学依据。上述计算表明，该企业的水解工序综合能力指数 MCp、MCpk均大于1，对照表1可知，企业工序能力状况符合要求，检验检疫部门可以按出口二类企业要求对其水解关键工序实施监管。

(2)检验检疫机构通过运用本方法能够深刻地认识和把握出口钛白粉企业企业水解工序能力状况，客观量化地给出工序的监管类别，有利于科学地开展日常监管，避免人为主观臆断，并根据工序实际状况，及时进行分类监管类别的调整，实施动态监管。

(3)出口钛白粉企业通过水解工序综合能力指数MCp、MCpk的计算结果，能够较好把握水解工序的技术管理，建立与出入境检验检疫机构对出口工业品生产监管模式相适应的质量控制手段，为进一步创造企业顺利出口钛白粉的宽松监管有利环境打下良好基础。

(4)为了获得生产工艺稳定状态下真实的原始质量指标数据，在保持生产条件基本稳定的情况下，应尽量减少样本抽样与测量的波动，避免出现较大误差。同时针对偏离正态分布的数据可采取一定方式进行数据转换，使转换后的数据符合正态分布［7］。

6 结语

本文通过多元统计分析方法在钛白粉化工生产中水解工序质量实例中的具体应用解决了水解工序能力的评价问题，为出入境检验检疫部门在广大的钛白粉出口企业中大力推行分类管理监管模式，以及强化对生产关键过程的监控提供了技术支持，也促使出口钛白粉企业加强水解工序的工艺指导和质量控制。

［1］ 李跃波.多元工序能力指数 Cpm［J］.武汉工业大学学报，1994，6(2):131 － 134.

［2］ 张益都.硫酸法钛白粉生产技术创新［M］.北京:化学工业出版社，2010，5:143 － 193.

［3］ 高凯，金广林.质量管理手册［M］.长春:吉林人民出版社，1994，7:7 － 14.

［4］ 柴永.正确地认识和使用过程能力指数Cp和Cpk［J］.中国质量，2007，2(2):79 － 81.

［5］ 钱道翠.综合评价主成分分析方法和因子分析方法的比较［J］.浙江统计，2004，(9):30 － 32.

［6］ 王少熙，贾新章，张玲.基于权重系数的多变量工序能力指数计算模型［J］.微电子学，2007，8(4):505 － 506.

［7］ 田志友，田澎，王浣尘.非正态过程能力指数研究中的几个问题［J］.工业工程，2005，1(1):29 － 32.