用解析法分析立辊轧机冲击振动信号
朱瑞荪,赵三星,杨 丹,饶 刚
(武汉科技大学机械自动化学院,湖北 武汉430068)
某钢铁公司立辊轧机轴承系统多次出现故障,为深入分析故障原因,需对轧机振动加速度信号进行分析,并对轧机振动状况做出评价.在咬钢、轧制和抛钢过程中,立辊轧机轴承系统在正交的三个方向上均承受着较大的振动冲击作用,轧机轴承系统的寿命受到严重影响.轧机振动是目前还未很好解决的世界性难题[1],是轧制生产率提高的一个重要障碍,也是造成设备破坏的一个重要因素.目前,针对机械设备振动和冲击的评价多采用统计方法,对振动频率、振动强度进行分析[2],或对设备振动加速度最大值、有效值、峰值因子、波形因子进行研究[3].文献[4]从信号处理角度研究了轧机振动特征,并用时域复指数法对轧机的模态参数进行了识别.
现场测试的轧机振动加速度信号包含着其工作状况的丰富信息,可据此对其寿命进行有效预测.根据国际标准ISO3945-1985,轧机轴承座振动速度的均方根值(有效值)可作为振动烈度评定标准[5].由于现场测试信号中含有较大噪声成份,且由测到的加速度信号变为速度、位移信号需经积分运算,若能根据测得的冲击振动加速度信号,识别出其解析表达式,无疑将具有较大优势.因为,这样一方面可消噪,另一方面也可根据加速度解析式得出振动速度,实现对轧机振动等级的准确判断.本文采用的把线性参数和非线性参数分开识别的算法,可达到该目的.
1 模型识别
假设振动模型

具有n个参变量.可将参变量分成两组:i个线性参数

j个非线性参数

显然,i+j=n.这样,可将该振动模型表示为

如果非线性参数取定值时,可根据最小二乘原理确定各个线性参数的大小.即模型输出与实测值间存在最小的差平方

式中M为采样点数.在σ取最小值时,应有
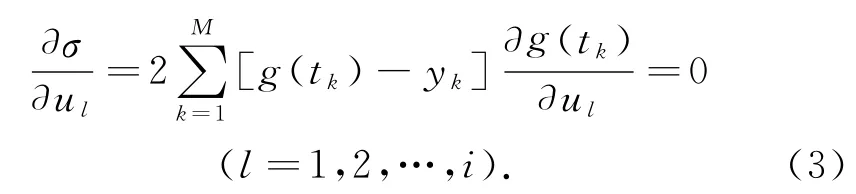
由式(1)可知,式(3)实际上是关于线性参数的线性方程组.因而在非线性参数取定值时,可据此确定线性参数.易得

这时模型变形为
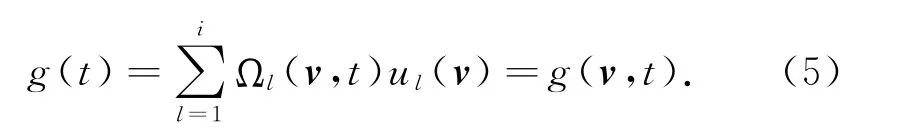
可见通过把线性参数和非线性参数分开识别,可使待识别的模型参数个数从i+j降为j.利用Gauss-Newton方法,可对待识别的j个模型参数进行识别.通过求解

对非线性模型参数修正.式中,y为实测信号向量;g(v)为模型输出向量;D为雅克比矩阵,其任一元素为

若要求出精确的雅克比矩阵是困难的,原因在于式(7)的第二项中的导数难以计算,在本研究中把其取为零.这虽会降低收敛速度,但该算法只需提供非线性参数初值(它们可通过具体情况分析确定),使模型识别变得容易.若不采用把线性参数和非线性参数分开识别的方法,由于线性参数初值给定较为困难,往往会遇到算法收敛问题;同时由于本算法使迭代过程识别参数数量大大降低,从另一方面提高了模型识别速度.具体识别过程可简述如下,首先给出非线性参数初值,根据式(4)得到线性参数,由式(7)得到雅克比矩阵,然后由式(6)算得非线性参数增量,进而对非线性参数修正.根据新的非线性参数,进入下一轮的迭代、修正过程,经过数轮运算,即可得到收敛的非线性参数,实现对复杂信号的参数识别.
2 立辊轧机冲击信号分析
以测得的立辊轧机轴承系统某一方向上的冲击振动加速度信号为例,验证笔者提出的识别算法的可靠性.由于该加速度信号可用

表达.可见,该冲击振动信号是由多个模态叠加而成的,其中的每个模态由阻尼系数αi、频率fi,以及幅值等参数确定.利用笔者提出的方法,仅需给出非线性参数

的初值,而无需确定线性参数

的初值.而各模态频率初值可通过对振动信号FFT分析后得到,阻尼系数初值可取零(αi取正值表明该模态振动衰减,取零表示振动稳定,而取负值表示振动发散).本算法可识别振动信号的解析表达式以及主要振动模态.从而容易得到振动速度的变化情况,实现对轧机系统振动的评价.
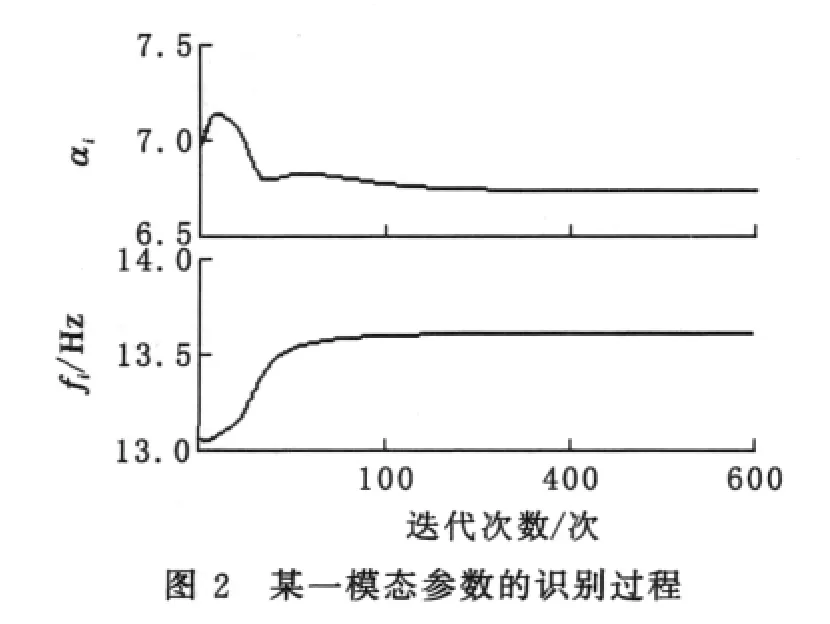
图1中的离散点表示轧机抛钢后沿铅垂方向的振动加速度实测信号.应用笔者提出的把非线性参数和线性参数分开识别的方法,可识别出如图1实线所示的加速度模型.可看出该模型输出与实测值十分接近.图2示出了该模型中的某一模态阻尼和模态频率的高精度识别过程.用解析法识别加速度信号,可去除噪声干扰,且易得到速度信号.
假设加速度

通过积分可以得到其速度
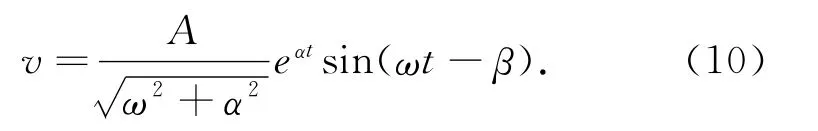

3 结束语
1)把模型线性参数和非线性参数分开识别,可避免对模型线性参数初值的选择,降低复杂模型识别的难度;
2)本算法可用于识别立辊轧机复杂的冲击振动加速度信号.根据得到的加速度解析表达式,经过一次和两次积分可得到其速度和位移信号,该方法具有较强的消噪能力;
3)本算法通过对轧机冲击振动信号的分析,可识别得到高精度的轧机系统振动模态参数.
[1]范小彬,臧 勇,王永涛,等.CSP轧机振动的测试与抑制[J].振动、测试与诊断,2007,27(2):156-158.
[2]机械工业部标准化研究所,机械振动与冲击国际标准译文集[M].北京:机械工业出版社,1984:78-94.
[3]王芬娥,曹新惠,郭维俊,等.联合收割机主驾驶座振动强度及其频率结构试验[J].农业机械学报,2007,38(4):62-65.
[4]臧 勇,范小彬,王会刚.基于信号时-频特征的轧机振动分析[J].振动、测试与诊断,2011,31(5):642-646.
[5]廖伯瑜.机械故障诊断基础[M].第一版.北京:冶金工业出版社,2007:85

