A Note on the Proof of the M oduli of Continuity for Stochastic Processes
ZHANG Jie-song
(School of Mathematical Sciences,Huaibei Normal University,235000,Huaibei,Anhui,China)
A Note on the Proof of the M oduli of Continuity for Stochastic Processes
ZHANG Jie-song
(School of Mathematical Sciences,Huaibei Normal University,235000,Huaibei,Anhui,China)
Abstract:There exists an ambiguous part in the proof ofmoduli of continuity and increments for stochastic processes in the article which was published on the Annals of Probability in 1992,while,this mistake can be remedied.In this paper,we give a specific proof by the method of decomposing and detailing.
Key words:stochastic processes;moduli of continuity;monotone nondecreasing
CLC number:O 211.4Document code:AArticle ID:2095-0691(2012)02-0015-03
1 Introducion
In many papers and monographs referring to the moduli of continuity of Wiener process,O-U process,fractional Wiener process etc.(e.g.[1-4]),a similar ambiguous conclusion is used.In other words,it is a mistake for us to consider that Ahis monotone nondecreasing.In fact,when h1≥h2,there is no inclusion between the region(0≤s≤1-h1,0≤t≤h1)and the region(0≤s≤1-h2,0≤t≤h2),so the function Ahwith respect to h may not be monotone nondecreasing.Here,we give a proof which does not use the ambiguous conclusion.
2 Some prelim inaries
Let B be a separable Banach space with norm‖‖ and let{Г(t),-∞<t<∞}be a stochastic process with values in B.Let P be the probability measure generated byΓ(·).Assume thatΓ(·)is P-almost surely continuous with respect to‖‖and that,with some t0,x*,h0,for|t|≤t0,0<x*≤x and 0<h≤h0,there exists a monotone nondecreasing functionσ(h)such that

with some K,γ,β>0.
Lemma 1[5]Assume that the stochastic process{Γ(t),-∞<t<∞}is as mentioned above and σ (·)is a regularly varying function at zero with a positive exponentα,namely
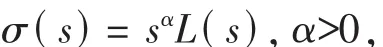
where L(·)is a slowly varying function at zero,that is,it is measurable,positive and

Then for anyε>0,there exist C=C(ε)>0 and 0<h0(ε)<1 such thatfor every x≥x*and 0<h≤h0(ε).
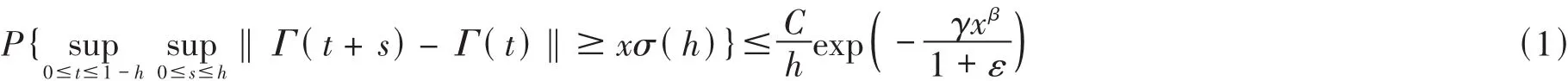
The inequality(1)can be extended to any finite interval(T1,T2),-∞<T1<T2<∞,as follows.
Lemma 2[5]Under the conditions of lemma 1,we have
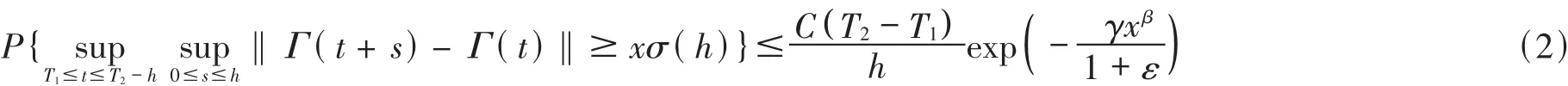
Remark The method of dealing with the difficulty caused by the generalization from the interval(0,1) to any finite interval(T1,T2)can refer to[6].
3 M oduli of continuity for stochastic processes
Theorem 1[5]Let{Γ(t),-∞<t<∞}and σ(h)be as in lemma 1.Then for any -∞<T1<T2<∞,we have
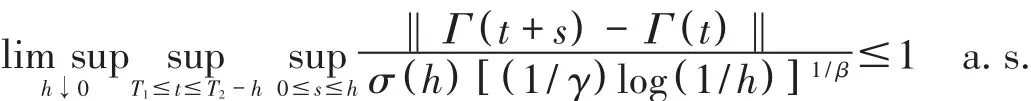
Proof Without loss of generality,we take T1=0 and T2=1.Now we let

and apply the inequality of(1)with x=(1+ε)2/β[(1/γ)log(1/h)]1/β>0.Then

ChooseΛ>1/εand let h=hn=n-Λ,then

and it follows from the Borel-Cantelli lemma that

for allε>0.
Because of(3),on considering now the case of hn+1<h<hn,and by letting Δhn=hn-hn+1,similar to [7],we have
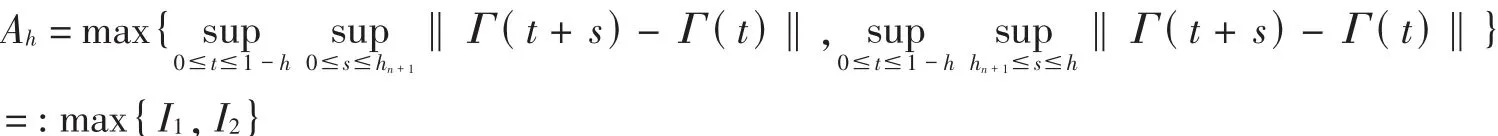
Obviously,I1≤Ahn+1,while,
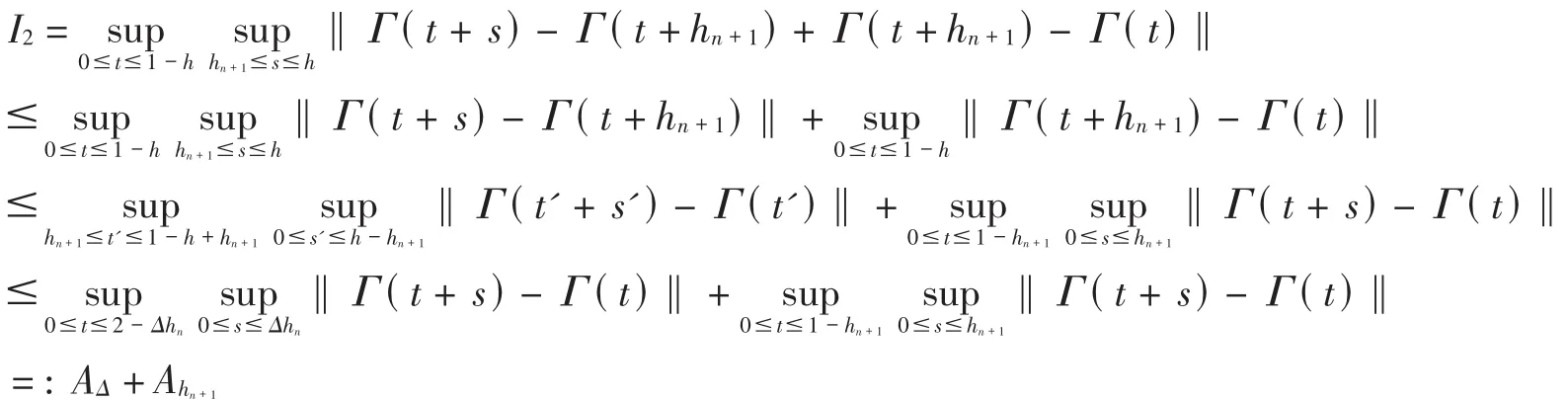
Hence

By the definition of hn,when n is sufficiently large,
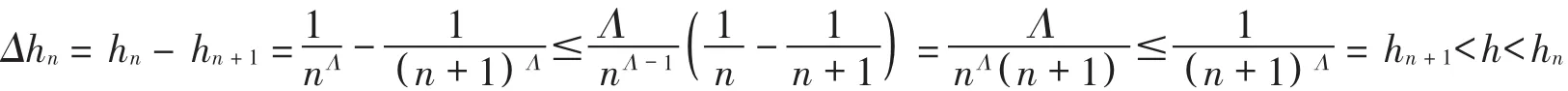
Apply the equality of(2)with x=(1+ε)2/β[(1/γ)log(1/Δhn)]1/β,ε>0,and taking T1=0,T2=2,then


And it follows from the Borel-Cantelli lemma that

Consequently,by the inequalities of(4),(5)and(6),we obtain
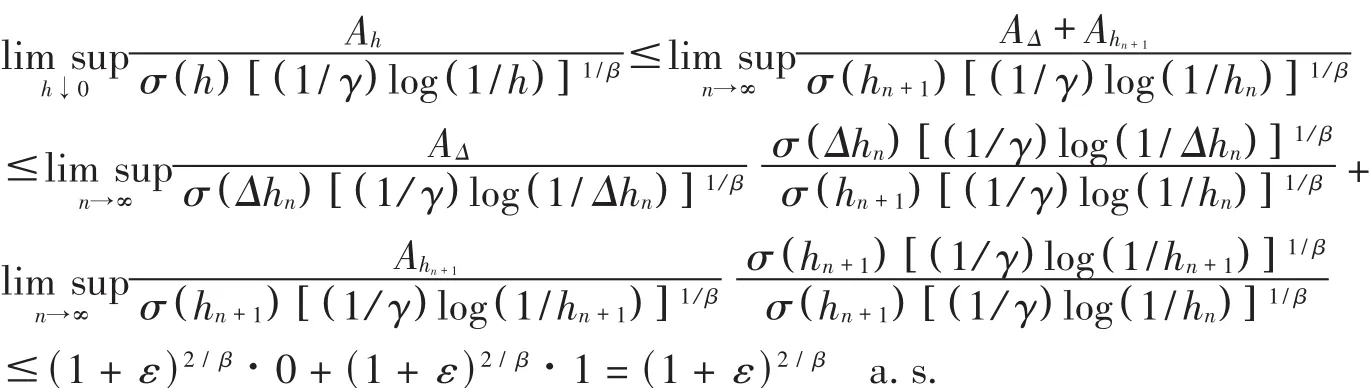
for allε>0,where the last inequality follows from the fact that for any given δ>0,when n is sufficiently large,then

and

This completes the proof of theorem 1.
[1]LIN Zhengyan,LU Chuanrong,SU Zhonggen.Foundation of the theory of probability limit[M].Beijing:Higher Education Press,1999.
[2]CSORGO M,REVESZ P.Strong approximations in probalility and stastistics[M].New York:Academic Press,1981.
[3]LIN Zhengyan,LU Chuanrong,ZHANG Lixin.Property of trajectory of Gauss processes[M].Beijing:Science Press,2001.
[4]CSAKI E,CSORGO M,LIN Zhengyan,et al.On infinite series of independent Ornstein-Uhlenbeck processes[J].Stochastic Process and their Applications,1991,39(1):25-44.
[5]CSAKIE,CSORGO M.Inequalities for increments of stochastic processes and moduli of continuity[J].Annals of Probability,1992,20(2):1 031-1 052.
[6]ZHANG Jiesong,YANG Lifeng.More result on the tail probability of Brown motion[J].Journal of Fuyang Teachers College:Natural Science,2008,25(1):29-31.
[7]MIAO Baiqi,LU Jun.A Note on the proof of the modulus of continuity of Wiener process[J].Journal of Huaibei Coal Industry Teachers College:Natural Science,1992,13(2):1-3.
关于随机过程连续模定理证明的一个注记
张节松
(淮北师范大学 数学科学学院,安徽 淮北 235000)
1992年发表在概率年刊上关于随机过程连续模及增量一文的证明中,存在一处模糊不清的地方,该漏洞是可以补救的,文章通过分解细化的办法给出一个确定的证明.
随机过程;连续模;单调不减
O 211.4
A
2095-0691(2012)02-0015-03
Recieved date:2011-09-09
Foundation item:The teaching and research project of Huaibei Normal University(jy09222)
Biography:ZHANG Jie-song(1981- ),male,native of Qianshan,Anhui,lecturer,master,major in probability limit.
