基于改进蚁群算法的单神经元PID控制在数控精校机电液伺服系统中的应用

任金霞，程 飞

(江西理工大学电气工程及自动化学院，江西赣州 341000)

基于改进蚁群算法的单神经元PID控制在数控精校机电液伺服系统中的应用

任金霞，程 飞

(江西理工大学电气工程及自动化学院，江西赣州 341000)

数控精校机电液伺服系统是一个参数变化比较大的非线性系统，常规的PID控制效果难以让人满意。采用单神经元PID控制器，在线调整权值，增强了对非线性系统的调节控制功能，然而参数的选择非常重要。文章提出一种改进的连续蚁群算法，用于优化单神经元PID控制器的参数，并用于精校机电液伺服系统，通过MATLAB仿真结果可得系统的阶跃响应，证明该算法比一般的蚁群算法精度更高，收敛更快，同时体现了该蚁群算法在实际应用中的实用性。

单神经元;精校机电液伺服系统;改进蚁群算法

0 引言

数控精校机是实现对轴类零件精密校直、提高轴类零件加工精度的关键设备［1-4］。由于工作过程中油温、负载等参数变化的影响，数控精校机电液伺服系统具有非线性、时变等不稳定性，常规的PID控制难以达到满意的控制效果［5-7］。

在本文中，采用单神经元PID控制器，通过在线调整加权系数来实现自适应、自组织的功能［5］，单神经元PID控制器参数的整定方法有很多种，例如文献［8-10］中用遗传算法整定单神经元PID控制器的参数，达到了很好的效果。分别用改进的连续蚁群算法和一般蚁群算法以及经验法优化改进控制器的学习速率和比例系数，使得系统更加快速达到稳定状态，且保证较小的超调量。文章通过MATLAB仿真软件验证了运用改进蚁群算法比一般蚁群算法对系统参数优化后。系统的时实控制效果更好，可靠性更高。

1 数控精校机电液伺服系统的结构

由图1中的结构框图所示，数控精校机电液伺服系统由工业计算机、D/A和A/D转换器，放大器，伺服阀，液压缸，位移传感器等部件组成的［2］。

当系统工作的时候，位移传感器实时记录下压头的位移量，然后通过A/D转换为数字量，再输送给工业计算机，工业计算机比较输入信号和反馈信号得到误差信号，接着再按控制算法进行控制，得到的控制信号经过D/A转换为模拟控制，最终控制压头的位置。

图1 数控精校机电液位置伺服系统的结构框架图

根据数控精校机电液伺服系统各元件的传递函数［2］，及性能参数，得到该系统的开环传递函数为:

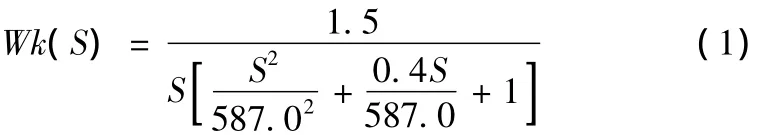
2 单神经元PID控制算法

单神经元PID控制算法的结构框图如图2所示。

图2 单神经元PID控制结构框图

该控制算法的表达式为:

其中wi(k)的算法表达式为:

输入状态x1，x2，x3的表达式为:x1(k)=e(k)，x2(k)=e(k)-e(k-1)，x3(k)=e(k)-2e(k-1)+e(k-2)。

其中z(k)=e(k)，r(k)为定状态，y(k)为输出状态，ηp，ηd，ηi为学习速率，K是神经元的比例系数，K＞0，ηp，ηi，ηd∈ (0，1)。

学习速率ηp，ηd，ηi和比例系数K一般都是根据经验值设定，从MATLAB仿真实验可知，经验法整定的参数值不一定最优，从而达不到控制要求。

3 基于改进蚁群算法的单神经元PID控制算法

3.1 基于网格划分策略的连续蚁群算法

基于网格划分策略的连续蚁群算法的基本思路为:首先根据要求解的连续优化问题的性质来估计所求变量的取值范围Xjlower≤Xj≤Xjupper(j=1，2，3，…n)。在变量范围内打网格，空间上的网格点对应了一个状态，每只蚂蚁在各个网格点之间移动，并根据此刻经过网格点的目标函数值产生不同的信息素，从而影响了后面蚂蚁的移动方向，循环了一段时间后，相邻节点间的评价函数值越好的网格点的信息素越大，接着找出信息量比较大的空间网格点，并将变量的取值范围逐渐缩小，在该点附近继续进行蚂蚁的移动，不断重复这样的过程，直到满足该算法的停止条件为止［3］。

3.2 基于网格划分策略的改进混沌蚁群算法

在本文中提出的改进蚁群算法是在以上叙述的基于网格策略的连续蚁群算法［3］的基础上，主要是融入混沌优化算法，分别在以下三个方面加以改进的。

第一个改进是在网格划分的时候，引入logistic混沌序列产生混沌变量如式(3)，得混沌序列x(i)，再根据每级产生的混沌序列产生混沌分布的网格点，而不是均匀分布，从而有利于蚁群搜索更具有遍历性，同时加快了收敛速度。每个网格点值为如下所示:

第二个改进是在网格划分结束后，蚁群在网格点移动，且留下信息素，循环一段时间，完成全局搜索，然后再缩小取值的变量范围▽，从而起到慢慢收敛的作用，在最好点附近进行搜索。在基于网格划分策略的蚁群算法中▽是设定好的恒定值。

在此将变量范围▽进行改进，将变量范围▽变成非自主设定的，而是随着迭代次数的增加而逐渐减小，其公式如下所示:

▽随迭代次数的变化的曲线如图3所示，图中，设a=10，b=50，Ncmax=100，可以看到经过改进后，▽就不再是固定不变的，从而范围缩小不再是恒定不变的，随着迭代次数的增加，范围越来越小了，且又在保证了一定的最小范围，从而加快了算法的收敛速度。

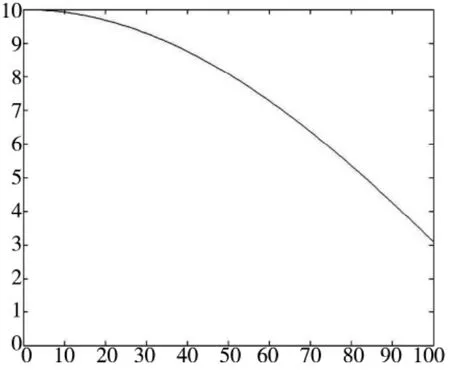
图3 ▽随迭代次数的变化的曲线图

第三个改进是在每次迭代结束后，蚂蚁全局搜索完毕，将函数值最小的的蚂蚁标记为最好蚂蚁，在最好蚂蚁附近再进行混沌搜索，若搜索到更好解，则替换为最优解。从而优化了该网格点的函数值，并且该最优解可以作为下一次迭代的参照物。有利于蚁群更快找到最优解。

3.3 基于改进混沌蚁群算法的单神经元PID参数优化

在工程应用中，评价系统动态特性一般使用偏差积分形式的性能指标。为了取得满意的动态特性，这里参数选择的目标函数采用偏差绝对值时间积分性能指标，并且加入控制输入的平方项，参数选取的目标函数为:

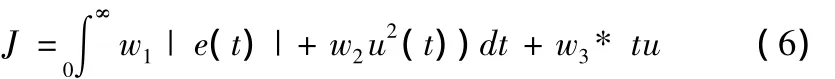
同时为避免产生超调，如果产生了超调，则把超调量也作为目标函数的一项。目标函数则为:

在(6)(7)式中，e(t)为误差，u(t)为控制器的输出，tu 为上升时间，w1，w2，w3为权值，erry(t)=y(t)-y(t-1)。在此。一般设置为:w1=0.999，w2=0.001，w3=2，w4=100。

采用改进混沌蚁群算法优化单神经元PID控制器的参数:学习速率 ηp，ηd，ηi和比例系数 K，使用如上所示的性能指标作为蚁群算法的目标函数。算法步骤为:

(1)初始化参数，估计出所求变量的取值范围:xjlower≤ xj≤ xjupper(j=1，2，…，n)。

(2)将各变量分成 N等分，hj=(xjupperxjlower)/N(j=1，2，…，n)。

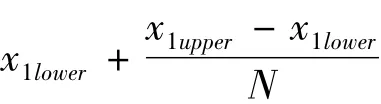
(5)根据蚂蚁经过的网格点，由网格点的值求出函数值。

(6)选出最优蚂蚁，在该蚂蚁附近进行混沌搜索，寻找最好蚂蚁标为f_best，以改蚂蚁经过的网格点 xi产生混沌序列y:xi=y1，yi+1=uyi(1-yi)，Yi=xlower+yi(xupper-xlower)。将所得目标函数值中的最小值为fb，若fb ＞ f_best，则f_best=fb，且更新其网格点的值;反之，f_best保持不变。

(7)重复(4)-(6);直到达到循环次数N。

(9)重复(2)～(8)，直到终止条件满足。

4 MATLAB仿真分析

根据本系统的数学模型，设采样周期为1ms，分别对带有基于改进蚁群算法的单神经元PID控制的系统和基于网格划分策略的蚁群算法优化的单神经元PID控制的系统以及一般单神经元PID控制的系统进行MATLAB仿真分析。

运用改进蚁群算法和一般蚁群算法优化的单神经元PID控制的目标函数值变化如图4所示。

用改进蚁群算法优化的单神经元PID控制器和常规单神经元PID控制器的阶跃响应曲线如图5所示。

图4 目标函数值的变化曲线

图5 单神经元PID控制的阶跃响应曲线

仿真结果如图4和图5所示，可以得到改进蚁群算法优化的单神经元PID控制器比一般蚁群算法优化的精度更优，且经过改进蚁群算法优化参数后的单神经元PID控制器比常规单神经元PID控制器的超调量更小，响应更快。

5 结束语

通过实例MATLAB仿真研究表明，采用改进蚁群算法对神经元PID控制器参数进行优化，是一种全局寻优方法，提高了计算效率和收敛速度，比单神经元PID控制器参数常规整定具有更好的响应特性，并且结构也比较简单，具有应用价值。

［1］陈永新.精校机电液位置伺服系统的研究［D］.合肥:合肥工业大学，2004.

［2］陆青松.数控精密校直机的研制开发及其液压伺服系统的研究［D］.合肥:合肥工业大学，2007.

［3］段海滨.蚁群算法原理及其应用［M］.北京:科学出版社，2005.

［4］吴卫平.基于神经网络的精校机液压位置伺服系统控制器的仿真与研究［D］.合肥:合肥工业大学，2009.

［5］刘金琨.先进PID及MATLAB仿真［M］.北京:电子工业出版社，2003.

［6］刘金琨.智能控制［M］.北京:电子工业出版社，2005.

［7］韩江，余仲元，何高清，等.模糊自适应整定PID控制在数控精密校直机电液伺服系统中的应用研究［J］.组合机床与自动化加工技术，2009(8):54-56.

［8］陈春兰，曾黄麟.一种基于遗传算法的单神经元PID控制器参数优化［J］.四川理工学院学报，2007(4):7-9.

［9］焦斌.遗传算法改进的单神经元PID控制器及其应用［J］. 上海机电学院学报，2005(3):6-8，23.

［10］叶军.基于改进遗传算法的单神经元自适应PID控制器［J］.机床与液压，2002(2):76-77.

The Application of the Single Neuron PID Control Based on Improved Ant Colony Algorithm in the Hydraulic-servo System of the Precise Straightening Press

REN Jin-xia，CHENG Fei
(School of Electronic Engineering＆ Automation Jiangxi University of Science and Technology，Ganzhou Jiangxi 341000，China)

The hydraulic-servo system of the precise straightening press is a nonlinear system whose parameters change largely，the effect of the conventional PID control makes it difficult satisfaction.The single neuron PID controller was taken，the relevance weights was adjusting online，the adjustment control function of the nonlinear system was strengthened，however the selection of parameters is very important.This paper puts forward an improved ant colony algorithm which was used to optimize the parameters of the single neuron PID controller and used in the hydraulic-servo system of the precise straightening press.The step response of the system was got by the matlab simulation results，it proved that the improved algorithm has the higher precise and the faster convergence than the average ant algorithm，and it reflected the practicality of the algorithm in the practical application.

the single neuron;the hydraulic-servo system of the precise straightening press;an improved ant colony algorithm

TH16;TG65

A

1001-2265(2012)12-0076-03

2012-04-10;

2012-05-08

任金霞(1970—)，女，山西孝义人，江西理工大学电气工程及自动化学院副教授，主要研究领域为智能控制、智能优化，(E-mail)dxzghyqq@sina.com。

(编辑 李秀敏)