基于改进粒子群算法的同*轴度误差评定及其可视化

翟旭军，张小萍，周圣铧

(1.江苏畜牧兽医职业技术学院机电工程系，江苏泰州 225300;2.南通大学机械工程学院，江苏南通 226019)

基于改进粒子群算法的同*轴度误差评定及其可视化

翟旭军1，张小萍2，周圣铧2

(1.江苏畜牧兽医职业技术学院机电工程系，江苏泰州 225300;2.南通大学机械工程学院，江苏南通 226019)

从定位最小包容区域定义出发，建立了同轴度误差数学模型，并将同轴度误差评定转化为圆柱度和圆度误差评定。针对基本粒子群算法容易出现前期搜索早熟收敛和后期搜索停滞振荡现象，通过引入异步变化的学习因子和线性递减的惯性权重系数，对其加以改进，并给出了利用改进粒子群算法进行同轴度误差评定的方法与步骤。同时通过实例实现了以VRML作为三维展示平台、以Java Applet作为控制核心的同轴度误差的评定及其结果可视化。实例证明:将改进的粒子群算法用于同轴度误差评定，有效提高了精度与效率;可视化的评定结果为工艺分析和改进提供了依据。

同轴度误差;定位最小包容区域;改进粒子群算法;可视化;VRML;Java Applet

0 引言

同轴度误差是指实际被测轴线相对基准轴线的变动量，它反映了同一零件上圆柱(锥)面的被测轴线与基准轴线应重合的精度要求。工程实际中，同轴度是衡量转动设备、回转零件制造与加工精度的重要指标之一。由于同轴度误差评定包含基准圆柱面轴线的确定和被测圆柱横截面圆心位置的确定两方面问题，国内外学者常把它归于圆柱度和圆度误差评定问题中讨论［1-4］，而单独讨论同轴度误差评定的文献并不多见。田树耀、黄富贵等［5］在分析了同轴度误差产生的原因后，将圆度误差的评定应用到同轴度误差的评定中，采用MATLAB软件提供的优化算法计算同轴度误差值，但文中只介绍了评定方法，并未给出实例进行算法的验证;沈先钊［6］采用符合最小区域法的最佳脊线法评定圆度、圆柱度及同轴度误差值，但文中也只以圆度误差评定为例介绍了该算法的评定过程，并未对同轴度误差评定作详细阐述;肖洒、郭慧［7］提出了含形状误差和不含形状误差的同轴度评定几何模型，并运用基本粒子群算法进行误差评定，数值求解仍转化为圆柱度误差计算进行。文献［8］中给出了满足定位最小包容区域定义的同轴度误差评定方法，但在实例计算时仍采用了最小二乘法与简化计算相结合。本文拟从定位最小包容区域定义出发，将改进的粒子群优化算法应用于同轴度误差评定，并通过实例验证评定的准确性及可行性。

1 改进的粒子群算法

粒子群优化算法是通过模拟鸟群觅食行为而发展起来的一种基于群体协作的随机搜索算法。与其它进化算法一样，也是基于“种群”和“进化”的概念，通过个体间的协作竞争，实现复杂空间最优解的搜索。由于具有很好的生物社会背景和较少的参数设置，易于理解和实现，得到了广泛的应用。但基本粒子群算法在搜索过程中，容易形成粒子种群的快速趋同效应，从而出现陷入局部极值、早熟收敛和搜索停滞现象。针对上述问题需要对基本粒子群算法进行改进，既要避免“早熟”现象的发生，又要加快收敛速度与效率。

1.1 粒子群算法基本原理

1.2 权重系数的线性递减

惯性权重ω是粒子群算法比较重要的参数。较大的ω便于全局搜索，避免陷入局部最优解;较小的ω利于算法收敛，能在当前搜索区域进行精确局部搜索。因此，针对基本粒子群算法容易早熟及算法后期易在全局最优解附近产生振荡的现象，可将权重系数作线性递减处理。惯性权重ω随算法迭代的变化公式为:

其中:ωmax、ωmin分别表示ω的最大值和最小值;tmax为最大搜索代数;t为当前搜索代数。

1.3 学习因子的异步变化

为了能使粒子在优化搜索的不同阶段，较好的完成全局开发与局部探索的工作，通过异步变化学习因子c1和c2，表现为在寻优的初始阶段，粒子应具有较大的自我学习能力和较小的社会学习能力，加强全局开发能力;在寻优的后期，粒子应具有较大的社会学习能力和较小的自我学习能力，加强局部探索能力。学习因子的异步变化公式为:

其中:c1，ini、c2，ini分别为c1和c2的初始值;c1，fin、c2，fin分别为c1和c2的迭代终值;tmax为最大搜索代数;t为当前搜索代数。

1.4 改进粒子群算法的性能测试

为了验证改进的粒子群优化(IPSO，Improved Particle Swarm Optimization)算法的精度和效率，可通过以下2个经典函数进行测试，并与惯性权重系数线性递减的粒子群优化(LDW-PSO，Linearly Decreasing Weight-PSO)算法［9］和飞行时间自适应调整的粒子群(FAA-PSO，Flying Time Adaptively Adjusted-PSO)算法［10］进行比较，观察改进的粒子群算法与其他算法在收敛速度和精度上的差异。

(1)Sphere函数，当xi=0时全局有最优值为0，设收敛精度为0.001。

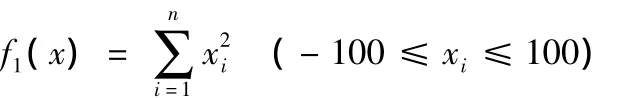
(2)Rastrigrin函数，当xi=0时全局有最优值为0，设收敛精度为0.001。

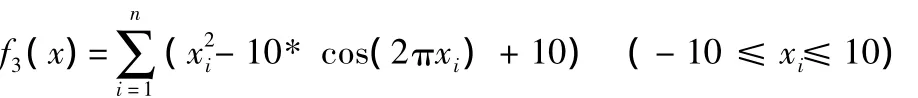
测试参数设置如下:粒子群规模为30;测试函数解空间维度为30;最大搜索代数为1000;改进的粒子群算法IPSO取最大惯性权重系数ωmax=1.2，最小惯性权重系数ωmin=0.2，学习因子c1和c2的初始值分别为2.5和0.5，学习因子c1和c2的迭代终值分别为0.5和2.5;LDW-PSO算法取 ωmax=0.9，ωmin=0.4;FAA-PSO取ωmax=1.0，ωmin=0.4。测试次数为50次，测试结果如表1所示。

表1 IPSO、LDW-PSO、FAA-PSO算法下测试函数运行结果对比表

从表1可以看出改进后的粒子群算法在精度和速度方面都优于其它两种算法。

2 基于改进粒子群算法的同轴度误差评判

2.1 同轴度误差的定义

同轴度误差是指实际被测轴线S相对于理想轴线的变动量，同轴度公差带的形状是直径为公差值t，且与基准轴线A同轴的圆柱面内区域，如图1。

图1 同轴度公差带示意图

2.2 同轴度误差数学模型

前已述及，同轴度误差评定的关键是能精确描述基准圆柱面轴线所在的位置和被测圆柱面圆截面圆心所在位置。本文从最小条件准则出发，建立基准圆柱面轴线方程和确定被测圆柱面圆截面圆心位置。

2.2.1 建立基准圆柱面轴线方程

假设基准圆柱面轴线方程为:

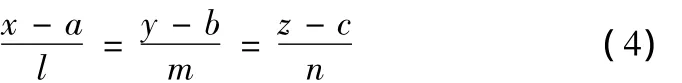
若基准圆柱面上的测点为P={Pi=(xi，yi，zi)|(i=0，1，2…p)}，测点到基准圆柱面轴线的距离为:

从定位最小包容区域定义出发，基准圆柱面轴线所在位置应满足下式:

其 中:dmax=max{di}(i=0，1，2，…，p)，dmin=min{di}(i=0，1，2，…，p)。

对于这样的非线性优化问题，采用改进的粒子群算法可获得高效解决，确定适应度函数为:

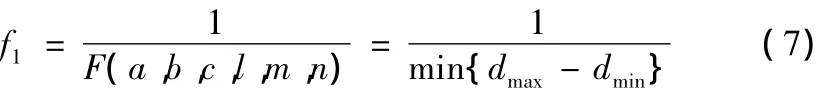
2.2.2 确定被测圆柱面圆截面圆心位置

假设被测圆柱面第k个圆截面方程为:

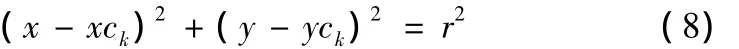
其中:下标k为被测圆柱面圆截面的索引，xck、yck为第k个圆截面圆心坐标，圆心的z坐标值与该圆截面其它测点z坐标值相等。

因此，被测圆柱在该圆截面的理论圆心位置应满足下式:

采用改进的粒子群算法搜索基准圆柱面轴线的精确位置时，确定适应度函数为:

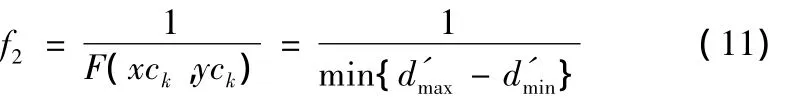
2.2.3 确定同轴度误差值

在确定了基准圆柱面轴线位置以及被测圆柱面各圆截面圆心位置后，根据公式(5)计算各圆心到轴线的距离最大值的2倍为同轴度的误差值，即:

2.3 同轴度误差评定步骤

Step1:参数的选择。选择粒子群规模N=30;最大惯性权重系数ωmax=1.2;最小惯性权重系数 ωmin=0.2;学习因子c1和c2的初始值分别为2.5和0.5;学习因子c1和c2的迭代终值分别为0.5和2.5;最大搜索代数为1000。

Step3:适应值的计算。根据求解基准圆柱面轴线位置适应度函数(7)和求解被测圆柱面各圆截面圆心位置适应度函数(11)确定粒子适应度值。

Step5:根据公式(2)更新惯性权重系数ω，根据公式(3)更新学习因子c1和c2。

Step6:根据公式(1)更新粒子速度和位置。

Step8:判断是否满足收敛条件。若满足则停止搜索，输出结果;若不满足则返回Step4继续搜索。

3 误差评定的可视化

通过上述同轴度误差的评定方法，可以准确快速地得到误差值，完成零件误差的合格性判断。同时为了能直观、形象地描述误差的分布规律，帮助企业查找误差产生原因，可将误差评定结果进行可视化处理，并可通过网络实现资源共享。

在众多的三维可视化平台(如OpenGL，Cult3D，3DSMAX，VRML等)中，VRML因其语法简单、文件容量小及平台无关性等优点成为网络三维描述语言的主流。本文拟在VRML平台上将各测点分布和相应的形位误差带直观显示出来。VRML 2.0建立三维场景的基本单元被称为节点，VRML中几何体的造型、对象的属性设置以及向外界获取或发送信息都需要依赖节点。下面仅对本文中用到的相关节点加以介绍［11］。节点的具体格式如下:

Shape节点可以用来定义三维形体，其geometry域值指定形体的具体形状，如用Sphere节点定义球体，可模拟误差评定中的各测点;用IndexedLineSet节点定义直线，可模拟基准轴线;用Extrusion节点定义圆柱面，可模拟同轴度误差最小包容区域。

VRML虽有良好的三维建模及展示功能，但自身与用户间交互功能有限。而JAVA作为一种功能强大的网络编程完全可以弥补VRML的不足。通过外部编程接口(External Authoring Interface，EAI)可实现VRML与Java Applet之间的通信，由外部程序控制三维场景的改变［12］。

基于VRML—Java Applet平台的同轴度误差可视化评定过程，可简单描述如下:①编写JAVA程序，完成误差评定界面设计与误差评定计算，并编译生成“*.class”文件;② 将编译的“*.class”文件与VRML文件同时嵌入到HTML文件，为VRML与Java Applet之间的通信搭建通道;③用户通过误差评定界面“读入数据”按钮，选择预先记录测点坐标的“*.txt”文档路径，录入相关数据;④通过误差评定界面“IPSO”按钮，进行误差计算;⑤误差评定界面“可视化”按钮功能是基于误差评定结果，实现其三维展示。

4 应用实例

以上介绍了同轴度误差的评定方法和步骤，现通过一实例加以验证。表2为某轴类零件上基准圆柱面轮廓测量点数据，表3为该零件上被测圆柱面圆截面轮廓测量点数据［8］。

表2 基准圆柱面轮廓测点数据(单位 /mm)

表3 被测圆柱面圆截面轮廓测点数据(单位 /mm)

文献［8］中对该组数据进行最小二乘法和简化计算处理，得到同轴度误差值为0.0238mm。采用改进的粒子群优化算法评定同轴度误差结果如图2所示，其误差值为0.0213mm，对应的基准圆柱面的轴线方程系数分别为(a，b，c，l，m，n)=(0.0033，0.0058，0.0611，1.5719e-6，1.0395e-5，-0.4792)。由此可见，本文提供的从定位最小包容区域定义出发评定同轴度误差的方法，结果更加精准，同时为企业或用户查找误差产生原因，改进后续工艺提供了依据。

图2 同轴度误差评定结果可视化界面

5 结束语

本文从形位误差的最小条件准则出发，建立了同轴度误差评定模型，并采用改进粒子群算法实现了误差值的精确求解。同时借助可视化技术直观、形象地模拟出误差结果，有助于企业在生产实践中后续工艺的分析与改进，进而减少零件的误收和误废，降低生产成本，提高生产效率。

［1］Liu J，Wang G L，Pan X D.Measurement system and evaluation approach for straightness error of valve sleeve inner hole［C］.International Conference on Measuring Technology and Mechatronics Automation.Changsha，China:IEEE Computer Society，2010:619-622.

［2］Utpal R，Xu Y X.Form and orientation tolerance analysis for cylindrical surfaces in computer aided inspection［J］.Computers in Industry，1995，26(2):127-134.

［3］Chen L J，Zhang Y，Liu P.Improvement of the traditional roundness measuring instrument［C］.Pro-ceedings of the ICPE'96＆6th SJSUT.Shenyang:Northeastern University Press，1996:363-366.

［4］Horikawa O，Maruyama N.A low cost high accuracy roundnessmeasuringsystem［J］.Precision Engineering，2001，25(4):200-205.

［5］田树耀，黄富贵，候学峰.一种新的同轴度误差评定方法及其误差分析［J］.工具技术，2008，42(5):82-85.

［6］沈先钊.圆度、圆柱度和同轴度计算机测量数据最小区域法处理算法研究［J］.中国机械工程，2003，14(17):1472-1473.

［7］肖洒，郭慧.基于粒子群算法的同轴度误差评定［J］.工具技术，2009，43(2):99-102.

［8］甘永立.形状和位置误差检测［M］.北京:国防工业出版社，1995.

［9］Shi Y，Eberhart R.A modified particle swarm optimizer［C］.IEEE World Congress on Computatio-nal Intelligence.Piscataway:IEEE Press，1998:69-73.

［10］张建科，刘三阳，张晓清.飞行时间自适应调整的粒子群算法［J］. 计算机应用，2006，26(10):2513-2515.

［11］张德丰，周灵.VRML虚拟现实应用技术［M］.北京:电子工业出版社，2010.

［12］魏园园，瞿畅，王君泽.网络环境下组合夹具虚拟转配平台的构建［J］.组合机床与自动化加工技术，2011(8):97-100.

Coaxiality Error Evaluation Based on Improved Particle Swarm Optimization and Its Visualization

ZHAI Xu-jun1，ZHANG Xiao-ping2，ZHOU Sheng-hua2
(1.Department of Mechanical and Electrical Engineering，Jiangsu Animal Husbandry and Veterinary College，Taizhou Jiangsu 225300，China;2.College of Mechanical Engineering，Nantong University，Nantong Jiangsu 226019，China)

Based on the definition of minimum locating zone，coaxiality error math model is established，and the evaluation of coaxiality error is transformed into cylindrical error and roundness error evaluation.As to the phenomenon that the basic particle swarm optimization algorithm is easy to appear premature convergence during the early search and stagnant oscillation in the later search，with the asynchronous changes in learning factor and the linearly decreasing inertia weight are introduced，the basic particle swarm optimization algorithm is modified.Then，the method and steps of coaxiality error evaluation using the improved particle swarm optimization algorithm are given.Simultaneously，with VRML as the 3D displaying platform and Java Applet as the controlling core，the visualization of coaxiality error evaluation was presented as an instance.And the result of the evaluation shows that it can raise the accuracy and efficiency of coaxiality error evaluation by using the improved particle swarm optimization algorithm.Also，it provides the basis for the process analysis and improvement.

coaxiality error;minimum locating zone;improved particle swarm optimization algorithm;visualization;VRML;Java Applet

TH161

A

1001-2265(2012)12-0055-05

2012-04-16

南通市应用研究计划资助项目(K2009022);江苏省泰州市科技发展计划项目(2011-TG1134)

翟旭军(1971—)，男，江苏兴化人，江苏畜牧兽医职业技术学院副教授、高级工程师，硕士，主要研究方向为CAD/CAM、虚拟制造和装配等;通讯作者:周圣铧(1987—)，男，江苏南通人，南通大学机械工程学院硕士研究生，主要研究方向为CAD/CAD、数字化制造、虚拟仿真技术及应用等，(E-mail)zsh_3415110@163.com。

(编辑 赵蓉)