低渗透油藏水力压裂井应力场转向定量评价

孙峰，李行船，熊廷松，张文豪

（1.中国石油大学（华东）储运与建筑工程学院，山东 青岛 266580；2.中国石化国际石油勘探开发有限公司，北京 100083；3.中国石油青海油田公司钻采工艺研究院，甘肃 敦煌 736202；4.中国石化中原油田分公司采油工程技术研究院，河南 濮阳 457001）

低渗透油藏水力压裂井应力场转向定量评价

孙峰1，李行船2，熊廷松3，张文豪4

（1.中国石油大学（华东）储运与建筑工程学院，山东 青岛 266580；2.中国石化国际石油勘探开发有限公司，北京 100083；3.中国石油青海油田公司钻采工艺研究院，甘肃 敦煌 736202；4.中国石化中原油田分公司采油工程技术研究院，河南 濮阳 457001）

基于多孔介质流-固耦合理论和有效应力定律，建立了孔隙压力与地应力相互作用的低渗透油藏水力压裂井应力场转向评价模型，采用有限元数值模拟技术并开发相应程序对耦合模型进行求解，定量分析了低渗透油藏开发过程中水力裂缝附近区域地应力场的变化特征。计算结果表明：水力裂缝导致近裂缝区域地应力场分布特征大幅度改变，沿裂缝与垂直裂缝方向应力场大小变化各向异性，应力场转向范围随初始水力裂缝长度增加而动态变化。

低渗透油藏；水力压裂；流-固耦合；地应力场转向；有限元数值模拟

低渗透油藏压裂开发过程中，由于高导流能力支撑裂缝影响，孔隙压力在裂缝周围呈椭圆形分布，沿水力裂缝方向的流体压力梯度变化远大于垂直裂缝方向，致使井筒和水力裂缝附近区域地应力场大小及方向发生大幅度改变［1-4］。综合考虑流体渗流与地应力变化之间的耦合作用，定量评价水力裂缝对地应力场分布格局的影响，对于当前低渗透油藏开发及重复压裂改造具有重要的指导作用［5-9］。本文在考虑低渗油藏水力压裂井近裂缝区域孔隙压力与地应力耦合作用［10-13］的基础上，建立了应力场转向评价模型，采用Galerkin有限元顺序解耦和参数迭代的方法求解耦合方程，应用裂缝单元处理水力裂缝与储层区域离散的网格尺度协调问题，定量模拟了水力裂缝附近区域地应力场的变化特征。

1 耦合模型方程

地应力场转向定量评价模型包括储层平衡方程和流体渗流方程。假设油藏为线弹性、均质连续、多孔介质系统，由储层骨架、孔隙流体2部分组成，孔隙介质中的流体运动符合达西定律。

1.1 储层平衡方程

影响储层平衡的地应力作用包括储层骨架有效应力和流体孔隙压力，其中骨架有效应力直接影响储层的受力变形。

储层骨架所受地应力、有效应力及流体孔隙压力之间的关系可表示为

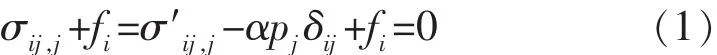
式中：σ，σ′分别为储层骨架所受地应力、有效应力，Pa；p为流体孔隙压力，Pa；α为 Biot系数；δ为Kronecker符号；f为体力，N/m3；i，j取值为1，2，3，代表空间的3个方向；j重复出现2次，表示该项在该指标的取值范围内遍历求和。

1.2 储层流体渗流方程

基于多孔介质流-固耦合理论，储层骨架变形影响流体压力的分布，耦合形式的单相饱和流体连续性方程为［14］

式中：ρf为流体密度，kg/m3；φ为孔隙度；εV为骨架体积应变；t为时间，s；K为渗透率，μm2；μ为流体黏度，Pa· s；q为源汇项，kg/（m3·s）。

式（1）、式（2）构成了低渗透油藏地应力场评价耦合模型的控制方程，但均为非线性的偏微分方程，且相互影响，难以求解。

1.3 耦合方程有限元公式

本文采用Galerkin有限元方法，在上述方程基础上引入“虚位移”，推导了耦合方程对应的等效弱积分方程。

对式（1）引入“虚位移”δu，考虑边界高斯积分变化，得到对应的等效弱积分形式为

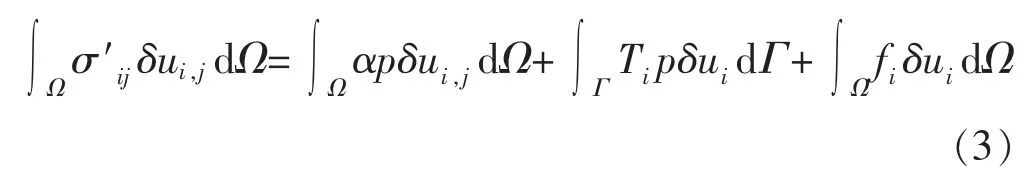
式中：Ω为求解区域；Γ为求解边界；T为边界力。

储层变形平衡的Galerkin有限元公式为

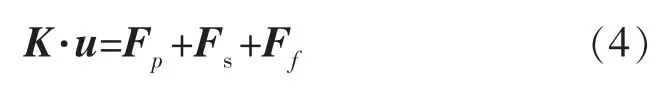
式中：K为方程刚度矩阵；u为方程变形矩阵；Fp，Fs，Ff分别为流体压力载荷、边界载荷和体积力载荷矩阵。

若考虑流体的微可压缩性，应用虚位移变分原理，可得式（2）的等效弱积分形式为

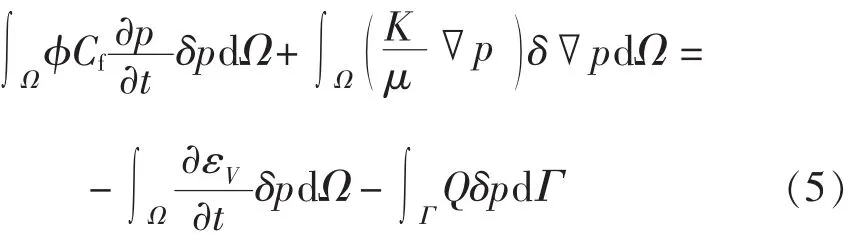
油藏流体渗流Galerkin有限元公式为

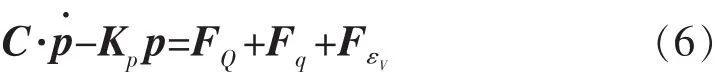
2 地应力场转向有限元模型

2.1 模型建立

采用上述流-固耦合模型，定量分析了在某低渗透油藏的压裂开发过程中，近裂缝区域内储层沿裂缝方向与垂直裂缝方向上应力差值及最大水平主应力方向的变化规律。

储层岩体物性参数为：弹性模量1.85×104MPa，泊松比0.25，孔隙度17.9%，最大、最小水平地应力分别为56.3，54.8 MPa，渗透率1.5×10-3μm2。储层流体物性参数为：流体黏度2.55 mPa·s，孔隙压力35 MPa，井底流压 20 MPa，Biot系数 0.85，裂缝导流能力 10 μm2·cm。

将水力压裂后形成的裂缝假设为理想翼对称裂缝，考虑结构的对称性，取计算单元的1/4部分建立有限元分析模型，并将井眼简化成一点，如图1所示。

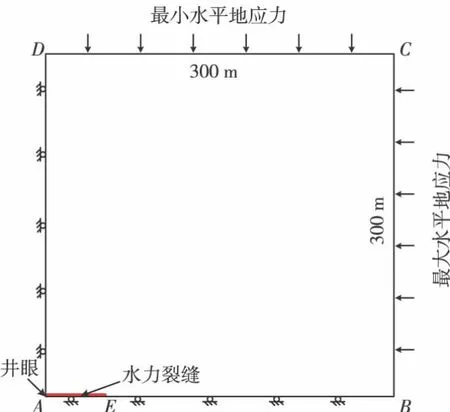
图1 有限元计算模型

2.2 耦合模型求解程序设计

在模型求解过程中，将程序划分为地应力和流体渗流2个计算模块，模块中有限元网格节点一一对应。地应力模块边界条件如图1所示，BC，CD边分别施加最大、最小水平地应力，AB，AD边分别施加位移约束条件。流体渗流模块中，在井眼A处施加井底流压条件，BC，CD为施加储层流体压力边界，AB，AD为流量封闭边界。

对于全耦合形式的有限元公式（4）和（6），采用储层变形—流体渗流顺序解耦的方法求解，用上一时间步的储层应力、应变迭代求解油藏的流体压力，通过耦合项数据循环迭代传递实现求解。

计算中将水力裂缝AE段处理为一维高导流裂缝杆单元［15］，将杆单元的质量、刚度矩阵变化叠加到连续储层单元的有限元方程项中，形成储层-裂缝组合单元模型，解决模拟分析中储层、裂缝网格尺度匹配问题。

3 结果分析

3.1 应力差值变化

井眼A处建立生产压差后，由于裂缝的高导流能力，沿裂缝方向的储层流体压力梯度变化远大于垂直裂缝方向，导致近裂缝区域储层沿裂缝方向的有效应力下降幅度大于垂直裂缝方向，应力场的方向发生偏转。随着孔隙压力的扩散传播，储层不同位置处，沿裂缝与垂直裂缝方向的应力差随时间增加而改变。

对应裂缝长度Lf为50 m、生产压差为15 MPa工况下，沿裂缝与垂直裂缝方向的应力差值变化见图2。由图2可以看出：

1）等值线数值小于0时，表明该区域内沿裂缝方向地应力小于垂直裂缝方向，最大水平主应力方向发生偏转。

2）数值为0的等值线为应力各向同性线，与沿井眼垂直裂缝方向交点处为应力各向同性点。模拟结果中，t为10，30 d时，应力差的应力各向同性点距井眼分别为9.7，14.3 m。

3）等值线数值大于0时，表明该区域内沿裂缝方向地应力大于垂直方向，应力场方向未发生偏转。

4）模拟工况下，水力裂缝附近发生应力场转向的区域范围随生产时间的增加而扩展。

3.2 最大水平主应力方向

Lf=50 m的近裂缝壁区域内，储层最大水平主应力场方向分布格局变化见图3。近裂缝区域最大水平主应力方向发生90°偏转，垂直井眼方向最大转向距离达到12.8 m。随着距裂缝距离的增大，储层流体压力梯度变化减小，最大水平主应力方向仍为水平方向。

Lf=100 m时最大水平主应力方向分布格局见图4。与储层有效应力大小变化对应，模拟裂缝长度100 m工况下最大水平主应力沿垂直裂缝方向发生偏转的距离增大，发生90°偏转的最大距离达到17.5 m。

计算结果表明：随裂缝长度增加，压力梯度沿裂缝方向的变化范围进一步扩展，最大水平主应力方向发生转向的范围增大。

图2 水力裂缝导致的应力差值变化

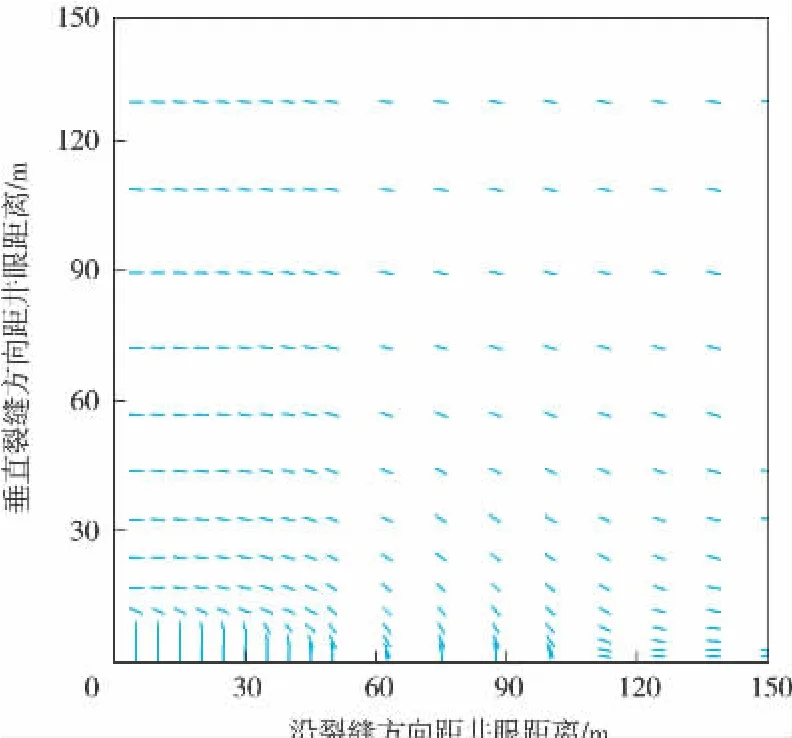
图3 Lf=50 m时最大水平主应力方向分布

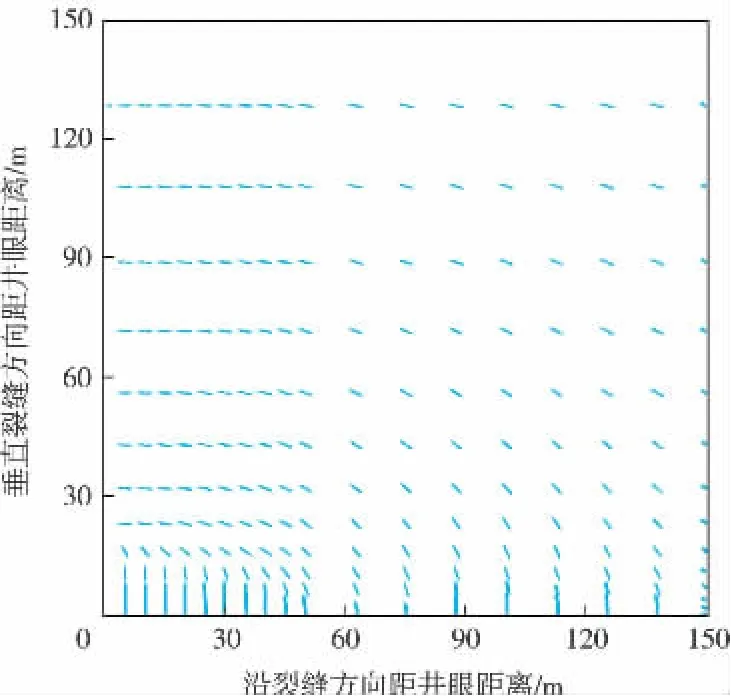
图4 Lf=100 m时最大水平主应力方向分布

4 结论

1）基于多孔介质流-固耦合理论和有效应力定律，建立了孔隙压力与地应力相互作用的低渗透油藏水力压裂井应力场转向评价模型，推导了模型对应的Galerkin有限元公式，采用顺序解耦和参数迭代的方法求解耦合方程。

2）由于裂缝的高导流能力，沿裂缝方向储层流体的压力梯度变化远大于垂直裂缝方向，导致近裂缝区域储层水平方向的有效应力下降大于垂直方向，最大水平主应力方向发生偏转，转向范围随初始裂缝长度增加而增大。

［1］ Siebrits E，Elbel J L，Detoumay E，et al.Parameters affecting azimuth and length of a secondary fracture during a refracture treatment［R］. SPE 48928，1998.

［2］ Siebrits E，Elbel J L，Hoover R S，et al.Refracture reorientation enhances gas production in Barnett shale tight gas wells［R］.SPE 63030，2000.

［3］ 刘洪，胡永全，赵金洲，等.重复压裂气井诱导应力场模拟研究［J］.岩石力学与工程学报，2004，23（23）：4022-4027.

［4］ 张广清，陈勉，姚飞，等.各向异性地层重复压裂最优化时机及影响因素分析［J］.石油学报，2008，29（6）：885-888.

［5］ 劳斌斌，刘月田，屈亚光，等.水力压裂影响因素的分析与优化［J］.断块油气田，2010，17（2）：225-228.

［6］ 艾敬旭，单学军，侯天江.五点井网注水井压裂裂缝参数对油井产量的影响［J］.断块油气田，2011，18（5）：649-652.

［7］ 吴超，刘建华.区域油田地应力及井壁稳定性综合预测方法［J］.断块油气田，2011，18（6）：705-709.

［8］ Aghighi M A，Ramhman S S，Rahman M M.Effect of formation stress distribution on hydraulic fracture reorientation in tight gas sands［R］. SPE 122723，2009.

［9］ Zhai Z Y，Sharma M M.Estimating fracture reorientation due to fluid injection/production［R］.SPE 106387，2007.

［10］刘建军，刘先贵，胡雅礽，等.低渗透储层流-固耦合渗流规律的研究［J］.岩石力学与工程学报，2002，21（1）：88-92.

［11］徐轩，杨正明，祖立凯，等.多重介质储层渗流的等效连续介质模型及数值模拟［J］.断块油气田，2010，17（6）：733-737.

［12］张广明，熊春明，刘合，等.复杂断块地应力场数值模拟方法研究［J］.断块油气田，2011，18（6）：710-713.

［13］Settari A，Walters D A.Advances in coupled geomechanical and reservoir modeling with applications to reservoir compaction［R］.SPE 51927，1999.

［14］Fung L S K.A coupled geomechanic multiphase flow model for analysis of in-situ recovery in cohesionless oil sands［J］.JCPT，1992，31（6）：56-67.

［15］孙峰，薛世峰，仝兴华，等.介质变形对低渗透油藏压裂产能影响有限元模拟［J］.石油学报，2010，31（5）：820-824.

（编辑 孙薇）

Quantitative evaluation on stress redistribution for hydraulic fracturing well of low-permeability reservoir

Sun Feng1,Li Xingchuan2,Xiong Tingsong3,Zhang Wenhao4
(1.College of Storage&Transportation and Civil Engineering,China University of Petroleum,Qingdao 266580,China;2.International Petroleum Exploration and Production Corporation,SINOPEC,Beijing 100083,China;3.Drilling and Production Technology Institute,Qinghai Oilfield Company,PetroChina,Dunhuang 736202,China;4.Research Institute of Oil Production Engineering Technology,Zhongyuan Oilfield Company,SINOPEC,Puyang 457001,China)

An evaluation model of stress redistribution for hydraulic fracturing well of low-permeability reservoir with the interaction of pore pressure and stress was established on the basis of fluid-solid coupling theory and effective stress principle for porous media. Coupled model was solved through the adaptation of finite element simulation and the development of relevant programme.The change feature of stress field around hydraulic fracture was quantitatively evaluated during the development of low-permeability reservoir.The computed results indicated that hydraulic fracture created the stress redistribution near fracture area was greatly changed,and that the size change of stress field showed the anisotropy along the fracture and vertical fracture direction and the area of stress redistribution was a function of initial hydraulic fracture length.

low-permeability reservoir;hydraulic fracturing;fluid-solid coupling;stress redistribution;finite element simulation

中国石油重大科技专项“低渗敏感储层渗流机理及增注技术研究”（2012-ZG-009）

TE319

A

10.6056/dkyqt201204020

2012-02-01；改回日期：2012-05-19。

孙峰，男，1979年生，讲师，博士，2010年毕业于中国石油大学（华东）地质资源与地质工程专业，现主要从事油气田地下工程力学研究。E-mail：hdpusf@163.com。

孙峰，李行船，熊廷松，等.低渗透油藏水力压裂井应力场转向定量评价［J］.断块油气田，2012，19（4）：489-492.

Sun Feng，Li Xingchuan，Xiong Tingsong，et al.Quantitative evaluation on stress redistribution for hydraulic fracturing well of low-permeability reservoir［J］.Fault-Block Oil&Gas Field，2012，19（4）：489-492.